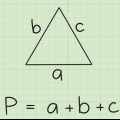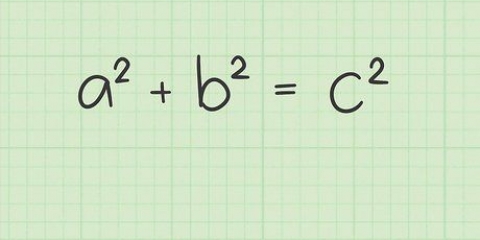Cómo determinar si tres longitudes juntas forman un triángulo: 6 pasos (con fotos)

Contenido

Pasos
Consejos

Determinar si las longitudes de tres lados juntos forman un triángulo es más fácil de lo que parece. Todo lo que tienes que hacer es usar el teorema de la desigualdad de triángulos, que establece que la suma de las longitudes de dos lados de un triángulo siempre es mayor que el tercer lado. Si esto se aplica a las tres combinaciones de las longitudes añadidas, entonces se trata de un triángulo.

Pasos

Imagen titulada Determine si las longitudes de tres lados son un triángulo Paso 1

1. Aprende el Teorema de la Desigualdad del Triángulo. Este teorema establece que la suma de dos lados de un triángulo debe ser mayor que el tercer lado. Si esto se aplica a las tres combinaciones, entonces tienes un verdadero triángulo. Tendrás que comprobar estas combinaciones, una por una, para asegurarte de que se puede formar un triángulo. También puedes considerar el triángulo como los lados de longitudes a, b y c, y el teorema como desigualdad: a+b > c, a+c > b y b+c > a.

Un ejemplo, a = 7, B = 10 y C = 5.

Imagen titulada Determine si las longitudes de tres lados son un triángulo Paso 2

2. Comprueba si la suma de los dos primeros lados es mayor que el tercero. En este caso puedes usar los lados a y B sumar, es decir, 7 + 10, para obtener 17, que es mayor que 5. También puedes pensar en ello como 17 > 5.

Imagen titulada Determine si las longitudes de tres lados son un triángulo Paso 3

3. Comprobar si la suma de la siguiente combinación de dos lados es mayor que el lado restante. Bueno, solo mira si la suma de los lados a y C es mayor que el lado B. Esto quiere decir que tienes que ver si 7 + 5, o 12, es mayor que 10. 12 > 10, entonces eso es correcto.

Imagen titulada Determine si las longitudes de tres lados son un triángulo Paso 4

4. Comprobar si la suma de la última combinación de dos lados es mayor que el lado restante. Tendrás que comprobar si la suma de los lados B y seda C es más grande que la seda a. Para ello, tendrás que comprobar si 10 + 5 es mayor que 7. 10 + 5 = 15 y 15 > 7, por lo que el triángulo es correcto para todos los lados.

Imagen titulada Determine si las longitudes de tres lados son un triángulo Paso 5

5. Revisa tu trabajo. Ahora que ha verificado todos los lados uno por uno, puede verificar nuevamente que la regla se aplica a las tres combinaciones. Si la suma de uno de los dos lados es mayor que el tercero en cualquier combinación, como en este triángulo, entonces has determinado que el triángulo es válido. Si la regla no se cumple ni siquiera para una combinación, entonces no es un verdadero triángulo. Dado que las siguientes afirmaciones son verdaderas, ha encontrado un triángulo válido:

a + b > C = 17 > 5

a + c > B = 12 > 10

b + c > a = 15 > 7

Imagen titulada Determine si las longitudes de tres lados son un triángulo Paso 6

6. Saber cómo encontrar un triángulo inválido. Solo para entenderlo, pero debes asegurarte de que puedes detectar un triángulo que no está bien. Suponga que está tratando con los siguientes tres lados y las longitudes: 5, 8 y 3. A ver si pasan la prueba:

5 + 8 > 3 = 13 > 3, por lo que este lado es correcto.

5 + 3 > 8 = 8 > 8. Porque esto no está bien, puedes parar ahora. esto no es un triangulo.