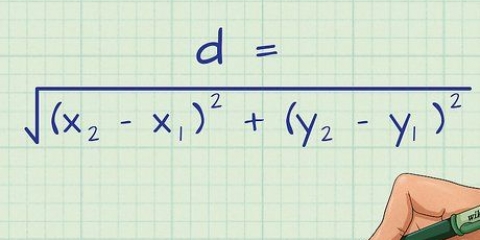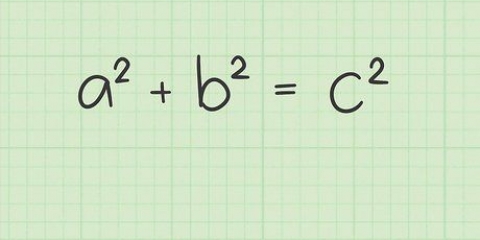Usar el teorema de Pitágoras: 12 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: la longitud de los lados de un triángulo rectángulo
- Método 2 de 2: Calcular la distancia entre dos puntos en el plano
Consejos

El teorema de Pitágoras describe la longitud de los lados de un triángulo rectángulo de una manera tan elegante y práctica que todavía se usa ampliamente en la actualidad. Esto establece que para cualquier triángulo rectángulo, la suma de los cuadrados de los lados derechos es igual al cuadrado de la hipotenusa. En otras palabras, para un triángulo rectángulo (un triángulo con lados que son perpendiculares entre sí), con lados de longitud a y b y una hipotenusa de longitud c: a + b = c. El teorema de Pitágoras es uno de los pilares de la geometría y tiene numerosas aplicaciones prácticas – por ejemplo, usando este teorema es muy fácil encontrar la distancia entre dos puntos en un plano.

Pasos

Método 1 de 2: la longitud de los lados de un triángulo rectángulo

Imagen titulada Usa el teorema de Pitágoras Paso 1

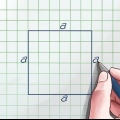
1. Comprueba si estás tratando con un triángulo rectángulo. El teorema de Pitágoras solo se puede usar para triángulos rectángulos, por lo que antes de continuar es importante establecer que su triángulo cumple con la definición de triángulo rectángulo. Afortunadamente, aquí solo hay un factor decisivo: una de las esquinas del triángulo debe ser un ángulo de 90 grados.

Una pista es que los ángulos rectos a menudo se marcan con un pequeño corchete para indicar que se trata de un ángulo de 90 grados. Vea si hay un soporte de este tipo en una de las esquinas de su triángulo.

Imagen titulada Usa el Teorema de Pitágoras Paso 2

2. Asigna las variables a, b y c a los lados de tu triángulo. En el teorema de Pitágoras, las variables a y b se refieren a los lados derechos de tu triángulo, y la variable c a la hipotenusa, el lado mayor opuesto al ángulo recto. Así que para empezar asignas las variables a y b (no importa el orden) a los lados rectos y le asignas c a la hipotenusa.

Imagen titulada Usa el Teorema de Pitágoras Paso 3

3. Determina qué lado del triángulo quieres saber. El teorema de Pitágoras te permite encontrar la longitud de cualquier lado de un triángulo, siempre que se conozcan dos de los lados. Determina cuál de los lados tiene una longitud desconocida--a, B, y/oC. Si solo uno es desconocido, entonces puedes seguir adelante.

Supongamos que sabemos que la hipotenusa tiene una longitud de 5 y uno de los otros lados tiene una longitud de 3. Se desconoce la longitud del lado restante. Como se conocen dos de los lados, podemos proceder a calcular la longitud del lado desconocido! Usaremos este ejemplo nuevamente más tarde.

Si la longitud de dos de los lados son desconocidos, entonces tienes que determinar la longitud de al menos un lado más para poder usar el teorema de Pitágoras. Las funciones trigonométricas básicas pueden ayudarte con esto, siempre que conozcas uno de los otros ángulos no rectos del triángulo.

Imagen titulada Usa el teorema de Pitágoras Paso 4

4. Calcula usando la ecuación y las conocidas. Inserta los valores de las longitudes de los lados de tu triángulo en la ecuación a + b = c. Recuerda que a y b son los lados rectos y c es la hipotenusa.

En nuestro ejemplo conocemos la longitud de un lado y la de la hipotenusa (3 & 5), entonces escribimos nuestra ecuación así: 3² + b² = 5²

Imagen titulada Usa el teorema de Pitágoras Paso 5

5. Calcula los cuadrados. Para resolver tu ecuación, comienza elevando al cuadrado cada uno de los lados conocidos. Si te resulta más fácil, puedes dejar la potencia y cuadrarla más tarde.

En nuestro ejemplo, elevamos al cuadrado 3 y 5 para obtener resp. 9 y 25 Llegar. Ahora podemos reescribir la ecuación como 9 + b² = 25.

Imagen titulada Usa el Teorema de Pitágoras Paso 6

6. Aislar la variable desconocida en un lado del signo igual. Opcionalmente, use operaciones algebraicas estándar para colocar la incógnita en un lado del signo igual y los cuadrados en el otro lado. Si está tratando de encontrar la hipotenusa, entonces c ya está en la posición de un lado, por lo que puede omitir ese paso.

En nuestro ejemplo, la ecuación ahora es 9 + b² = 25. a b² restamos 9 de ambos lados de la ecuación. Esto nos deja con b² = 16.

Imagen titulada Usa el teorema de Pitágoras Paso 7

7. Saca la raíz cuadrada de ambos lados de la ecuación. Ahora debería tener un cuadrado (variable) en un lado de la ecuación y un número en el otro lado. Ahora resta la raíz cuadrada de ambos lados para encontrar la longitud de la incógnita.

En nuestro ejemplo, b² = 16, la ecuación después de sacar raíces cuadradas es b = 4. Entonces podemos decir que la longitud del lado desconocido de nuestro triángulo es igual a 4.

Imagen titulada Usa el teorema de Pitágoras Paso 8

8. Usar el teorema de Pitágoras en la práctica. La razón por la que se usa tanto el teorema de Pitágoras es porque es aplicable para resolver muchos problemas prácticos. Aprende a reconocer triángulos rectángulos en el mundo que te rodea: siempre que puedas identificar un triángulo rectángulo con uno o más objetos, el teorema de Pitágoras se puede usar para encontrar la longitud de uno de los lados, siempre que haya dos lados o ángulos.

Tomemos un ejemplo del mundo real. Una escalera se apoya contra una pared. La parte inferior de la escalera está a 5 metros de la pared. La escalera llega hasta 20 metros medidos desde el fondo de la pared. cuanto mide la escalera?

"5 metros es la distancia a la pared” y "la escalera tiene 20 metros de altura”. Esto da una indicación de la longitud de los lados del triángulo. Como se supone que la pared y el suelo forman un ángulo recto y la escalera forma un ángulo diagonal con la pared, podemos considerar esta disposición como un triángulo rectángulo, cuyos lados tienen una longitud de a = 5 y b = 20. La longitud de la escalera es la hipotenusa, la variable desconocida c. Apliquemos aquí el teorema de Pitágoras:

a² + b² = c²

(5)² + (20)² = c²

25 + 400 = c²

425 = c²

sqrt(425) = c

c = 20,6 . La longitud de la escalera es (aproximada) 20,6 metros.

Método 2 de 2: Calcular la distancia entre dos puntos en el plano

Imagen titulada Usa el teorema de Pitágoras Paso 9

1. Definir dos puntos en el plano. El teorema de Pitágoras se puede utilizar muy fácilmente para determinar la distancia en línea recta entre dos puntos en el plano. Todo lo que necesitas son las coordenadas x e y de dos puntos cualesquiera. Por lo general, estas coordenadas se escriben como (x, y).

Para hallar la distancia entre estos dos puntos, consideramos cada uno de los puntos como uno de los vértices de un triángulo rectángulo, que no pertenecen al ángulo recto. Esto hace que sea muy fácil encontrar la longitud de a y b, después de lo cual se puede calcular c (la hipotenusa y la distancia entre los dos puntos).

Imagen titulada Usa el teorema de Pitágoras Paso 10

2. Trace los dos puntos en un gráfico. En un plano X-Y, para cada punto (x, y), x es un punto en el eje x horizontal e y es un punto en el eje y vertical. Puedes encontrar la distancia entre los dos sin graficarlos, pero hacerlo te dará una referencia visual para verificar si tu respuesta tiene sentido.

Imagen titulada Usa el teorema de Pitágoras Paso 11

3. Encuentra la longitud de los lados rectos de tu triángulo. Al considerar tus dos puntos como los ángulos del triángulo adyacente a la hipotenusa, puedes encontrar las longitudes de los lados a y b. Puede hacer esto usando el gráfico o usando las fórmulas |x₁ - X₂| para el lado horizontal y |y₁ - y₂| para el lado vertical, donde (x₁,y₁) es el primer punto y (x₂,y₂) el segundo punto.

Supongamos que tenemos los puntos (6.1) y (3.5). La longitud del lado horizontal de nuestro triángulo es:

|x₁ - X₂|

|3 - 6|

| -3 | = 3

La longitud del lado vertical es:

|y₁ - y₂|

|1 - 5|

| -4 | = 4

Entonces podemos decir que la longitud de los lados de nuestro triángulo rectángulo es igual a a = 3 y b = 4.

Imagen titulada Usa el teorema de Pitágoras Paso 12

4. Usa el teorema de Pitágoras para encontrar la hipotenusa. La distancia entre los dos puntos es la longitud de la hipotenusa del triángulo. Usa el teorema de Pitágoras para encontrar la hipotenusa del triángulo, con lados a, b y c.

En nuestro ejemplo, conocemos los puntos (3,5) y (6.1), y las longitudes de los lados son a= 3 y b=4, por lo que determinamos la hipotenusa de la siguiente manera:

(3)²+(4)²= c²

c= sqrt(9+16)

c= sqrt(25)

c= 5. La distancia entre (3.5) y (6.1) es 5.

Consejos

Si el triángulo no es un triángulo rectángulo, entonces no puedes simplemente usar el teorema de Pitágoras.
La hipotenusa siempre es:

la recta opuesta al ángulo recto
el lado más largo del triángulo rectángulo
La variable C en el teorema de Pitágoras

sqrt(x) significa "la raíz cuadrada de x".

No olvides revisar siempre tus respuestas. Si parece que una respuesta no es correcta, revise sus cálculos o comience de nuevo.

Si solo conoce un lado del triángulo, pero también uno de los otros ángulos (que no sea el ángulo recto), primero calcule otro lado usando lo que sabe sobre trigonometría (sen, cos, tan) o las proporciones 30-60-90 / 45-45-90.

Otra verificación: el lado más largo se opone al ángulo más grande y el lado más corto se opone al ángulo más pequeño.