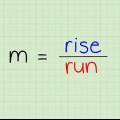Usar la fórmula de la pendiente

Contenido

Pasos
Consejos

La fórmula de la pendiente es una forma común de escribir una ecuación lineal. Esta fórmula se escribe como "y = mx + b" – donde a las letras se les da un valor determinado para poder resolver esta ecuación, o donde se resuelve la ecuación para encontrar los valores de las variables. Entonces: "X" y "y" son los "X-" y "y"-coordenadas de una recta, "metro" es la pendiente (pendiente), la relación (cambio de y)/(cambio de x), y "B" es la intersección con el eje y. Si quieres saber cómo usar la fórmula de la pendiente, has venido al lugar correcto.

Pasos

Método 1 de 5: usa la fórmula de la pendiente para los problemas

Imagen titulada Usar la forma de intersección de la pendiente (en álgebra) Paso 1

1. Leer la tarea. Antes de que pueda continuar, debe leer la tarea cuidadosamente para que comprenda exactamente lo que se le pide. Lea la siguiente declaración: Su cuenta bancaria aumenta linealmente cada semana. Si tiene $560 en su cuenta bancaria después de 20 semanas de trabajo y $585 después de 21 semanas, ¿cómo expresa la relación entre la cantidad que ganó y cuántas semanas trabajó utilizando la fórmula de la pendiente?.

Imagen titulada Usar la forma de intersección de la pendiente (en álgebra) Paso 2

2. Piense en el problema en términos de la fórmula de la pendiente. Debes escribirlo así: y = mx + b. La variable "metro" es la pendiente y "B" es el punto de partida donde la línea se cruza con el eje y. Tenga en cuenta que el problema establece que, " Su cuenta bancaria aumenta linealmente cada semana," lo que significa que ahorra la misma cantidad cada semana, lo que a su vez significa que tiene una línea recta e inclinada. Ese "constante," y el plan de ahorro uniformemente continuo es lo que lo hace lineal. Si no ahorra la misma cantidad cada vez, no es lineal.

Imagen titulada Usar la forma de intersección de la pendiente (en álgebra) Paso 3

3. Encuentra la pendiente de la recta. Para encontrar la pendiente necesitas poder determinar la tasa de cambio. Si empiezas con 560€ y la semana siguiente tienes 585€, entonces has ganado 25€ después de 1 semana de trabajo. También puedes calcularlo restando 560€ a 585€. 585-560 = 25.

4. Encuentre la intersección con el eje y. Para encontrar esta intersección, también llamada "B" en y = mx + b, necesita saber el punto de partida de su problema (que es la intersección con el eje y). Esto significa que tienes que averiguar con cuánto dinero comenzaste. Si tenía $560 después de 20 semanas de trabajo y sabe que ganó $25 en una semana, use la siguiente multiplicación para calcular cuánto ganó en 20 semanas. 20 x 25 = 500, entonces ganaste $500 en esas semanas.

Porque después de 20 semanas tienes 560 € y también has ganado 500 €. entonces sabes cuánto empezaste restando 500 de 560. 560 - 500 = 60.

Entonces el "B" o el punto de partida, es 60.

5. escribe la ecuacion. Ahora que conoce la pendiente, m es 25 (ganando 25 dólares por semana) y el punto inicial b es 60, puede introducir esto en la ecuación:

y = mx + b

y = 25x + 60

6. Prueba si la ecuación es correcta. El "y" es la cantidad de dinero que has ganado y el "X" el número de semanas que ha trabajado. Vea cuánto dinero ha ganado en un número determinado de semanas ingresando estos datos en la ecuación. Pruebe dos ejemplos:

cuanto dinero ganaste en 10 semanas? llenar "10" en para el "X" para averiguar aquí.

y = 25x + 60 =

y = 25(10) + 60 =

y = 250 + 60 =

y = 310. Después de 10 semanas has ganado 310€.

¿Cuántas semanas hay que trabajar para ganar 800 euros?? llenar "800" en para el "y"-variable de la ecuación para atrasar el valor de "X" venir.

y = 25x + 60 =

800 = 25x + 60 =

800 - 60 =

25x = 740 =

25x/25 = 740/25 =

x = 29.6. Puedes ganar 800 euros en unas 30 semanas.

Método 2 de 5: convertir una ecuación a la fórmula de la pendiente

1. escribe la ecuacion. Supongamos que se trata de la siguiente ecuación, 4y +3x = 16.

2. Aislar el término y en un lado de la ecuación. Haces esto restando 3x de ambos lados de la ecuación. La ecuación ahora debería verse así: 4y = -3x +16.

4y + 3x = 16

4y + 3x - 3x = 16 -3x

4y = -3x +16

3. Divide todos los términos por el coeficiente de y. Este es el número para la variable y. No pongas un número aquí, entonces ya terminaste. Si hay un número (el coeficiente), divide cada término de la ecuación por ese número. En este caso, el coeficiente y es 4, por lo que debe dividir 4x, -3x y 16 entre 4 para obtener la respuesta final. Así es como funciona esto:

4y = -3x +16 =

/₄y = /₄X +/_{4 = (por división)}

y = /₄X + 4 (simplificando la división)

4. Determinar los términos en la ecuación. Cuando uses la ecuación para dibujar una línea, recuerda que "y" la coordenada y es en "-3/4" la cuesta o pendiente, "X" es entonces las coordenadas x y "4" la intersección con el eje y.

Método 3 de 5: La fórmula de la pendiente usando un punto y la pendiente

1. Escribe la ecuación de la línea como la fórmula de la pendiente. Solo escribe primero y = mx + b. Luego puede completar la ecuación una vez que tenga suficientes datos. Suponga que desea resolver el siguiente problema: Encuentra la ecuación de una recta con pendiente 4 que pasa por el punto (-1, -6).

2. Completa los detalles. Tú lo sabes "metro" es igual a la pendiente de la recta, es igual a 4 y eso "y" y "X" respectivamente el "X" y "y" las coordenadas son. En este caso, los datos son "X" = -1 y "y" = -6. "B" representa la intersección con el eje y; este valor aún no se conoce. Así es como se ve ahora la ecuación:

y = -6, m = 4, x = -1 (los valores dados)

y = mx + b (la fórmula)

-6 = (4)(-1) + b (después de completar)

3. Resolver "B". Ahora es cuestión de hacer ejercicio "B," encontrar la intersección con el eje y. Multiplica 4 y -1 y luego resta el resultado de -6. Así es como se hace:

-6 = (4)(-1) + segundo

-6 = -4 + segundo

-6 - (-4) = -4 -(-4) + segundo

-6 - (-4) = b (término simplificado a la derecha)

-2 = b (término a la izquierda simplificado)

4. escribe la ecuacion. Ahora tu "B," puede completar los valores necesarios en la fórmula de la pendiente. Todo lo que necesitas saber es la pendiente y la intersección con el eje y (b):

m = 4, b = -2

y = mx + b

y = 4x -2 (sustitución)

Método 4 de 5: escribir la fórmula de la pendiente usando dos puntos

1. Escribe los dos puntos. Antes de que puedas hacer la ecuación de la recta, primero escribes los dos puntos que se dan. Suponga que desea resolver el siguiente problema: Encuentra la ecuación de la recta que pasa por los puntos (-2, 4) y (1, 2).

2. Usa estos puntos para encontrar la pendiente de la ecuación. La fórmula para determinar la pendiente de la recta que pasa por dos puntos es (y₂ - y₁) / (X₂ - X₁). Estás tratando con las coordenadas (x₁, Y₁) = (-2, 4) y (x₂, Y₂ ) = (1, 2). Ahora inserte este valor en la ecuación y resuelva para m.

(y₂ - y₁) / (X₂ - X₁) =

(2 - 4)/(1 - -2) =

-2/3 = metro

La pendiente de la recta es -2/3.

3. Elija uno de los puntos para resolver la intersección con el eje y. No importa qué par elijas. Elija el que le resulte más fácil para trabajar Supongamos que elige el punto (1, 2). Ahora llena esto en la ecuación "y = mx + b". Resolver "B":

y = 2, x, = 1, m = -2/3

y = mx + b

2 = (-2/3)(1) + segundo

2 = -2/3 + segundo

2 - (-2/3) = segundo

2 + 2/3 = b, o b = /₃

4. Completando los números en la ecuación original. Ahora que sabes que la pendiente es igual a 2/3 y la intersección con el eje y ("B") es igual a 2 2/3, puedes sustituir estos valores en la ecuación original de la recta y listo.

y = mx + b

y = /₃X + 2 2/3

Método 5 de 5: dibujar la línea

1. Escribe la ecuación y utilízala para dibujar la recta. Supongamos que tiene la siguiente ecuación: y = 4x + 3.

2. Comience con la intersección con el eje y. La intersección con el eje y viene dada por "+3" o "B" en la ecuacion. Este es el punto (0, 3). Indique este punto con un punto.

3. Usa la pendiente de la línea para encontrar las coordenadas del otro punto. Porque sabes que la pendiente está representada por "metro=4," puedes decir que la pendiente es igual a y/x=4/1. Esto significa que cada vez que la línea sube 4 puntos en el eje y, se desplaza 1 punto a la derecha en el eje x. Entonces, comienzas en el punto (0, 3) y subes 4 puntos y 1 punto a la derecha, terminando en el punto (1, 7) como el siguiente punto de la línea.

Si la pendiente es negativa, la recta desciende de izquierda a derecha.

4. Conecta los dos puntos con una línea. Usa un lápiz y una regla para esto. Esto es todo lo que necesitas hacer y has dibujado una línea perfecta de acuerdo con la ecuación dada. Dos puntos son suficientes para trazar la línea. Si es necesario, compruébelo dibujando algunos puntos más.

Consejos

Un ejemplo de disminución y aumento lineal es el cambio constante de la velocidad de un objeto, medida en metros por segundo, distancia medida en el tiempo.
Álgebra está activa. No solo tienes que leer y entender la teoría, también tienes que trabajar con ella para entender cómo funciona.
Esta es la forma real de demostrar que entiendes: el cambio de y en comparación con el cambio de x se denomina aumento (crecimiento) o disminución (decaimiento) de la diferencia de y dividida por la diferencia de x. Dividir por también se llama razón, fracción o razón. Aquí está la relación "el grado de cambio.
Al principio, resuelva también los ejercicios simples en papel. Si trabajas en ejercicios más difíciles en una etapa posterior, te beneficiarás mucho de este método porque te da una mejor idea del procedimiento a seguir para hacer un gráfico.
Recuerda: la multiplicación viene antes de la suma, así que y = mx + b; entonces primero m × x y luego x+b.
No te limites a leer los ejemplos. Anótalos y practica los diferentes pasos para que entiendas bien todo el proceso.
Seguro que impresionarás a tu profesor si aprendes a entender cómo aplicar una ecuación lineal a todo tipo de problemas.
El sistema de coordenadas cartesianas utilizado en álgebra para hacer un gráfico, etc. lleva el nombre de su inventor francés, usándolo para coordenadas en mapas. Se utilizan sistemas similares en varias áreas de las matemáticas, así como en astronomía, navegación, pantallas de computadora, letreros de neón y marcadores, o para ubicar casi cualquier cosa.
La pendiente de una línea mide la relación del cambio vertical (y) en comparación con el cambio horizontal (x). Puede tratarse de puntos en una línea, pero también de una determinada tasa de crecimiento lineal o de la pendiente de una colina.