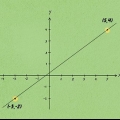
El eje x es el eje horizontal; el eje y es el eje vertical. Las coordenadas de un punto se escriben como  .
. Por ejemplo, un segmento de línea puede tener un punto final en  y otro en
y otro en  .
. 
Por ejemplo, con los puntos  y
y  , su fórmula se verá así:
, su fórmula se verá así: 


Por ejemplo:



Por ejemplo:



Dado que está determinando la raíz cuadrada, es posible que deba redondear su respuesta. Dado que está trabajando desde un sistema de coordenadas, su respuesta será en general "unidades" y no en centímetros, metros o cualquier otra unidad. Por ejemplo:

 unidades.
unidades.
Cálculo de la longitud de una línea usando la fórmula de la distancia
Puede medir la longitud de una línea vertical u horizontal en un sistema de coordenadas simplemente sumando las coordenadas; sin embargo, medir la longitud de una línea diagonal es un poco más complicado. Puedes usar la fórmula de la distancia para determinar la longitud de dicha línea. Esta fórmula es en realidad el teorema de Pitágoras, que queda claro cuando imaginas el segmento de línea como la hipotenusa de un triángulo rectángulo. Mediante el uso de una fórmula geométrica simple, medir líneas a lo largo de un número de coordenadas se convierte en una tarea relativamente simple.
Pasos
Parte 1 de 2: escribir la fórmula

1. Escribe la fórmula de la distancia. La fórmula establece que  , por lo cual
, por lo cual  es igual a la distancia de la recta,
es igual a la distancia de la recta,  es igual a las coordenadas del primer punto final del segmento de línea, y
es igual a las coordenadas del primer punto final del segmento de línea, y  es igual a las coordenadas del segundo punto final del segmento de línea.
es igual a las coordenadas del segundo punto final del segmento de línea.
 , por lo cual
, por lo cual  es igual a la distancia de la recta,
es igual a la distancia de la recta,  es igual a las coordenadas del primer punto final del segmento de línea, y
es igual a las coordenadas del primer punto final del segmento de línea, y  es igual a las coordenadas del segundo punto final del segmento de línea.
es igual a las coordenadas del segundo punto final del segmento de línea.
2. Determinar las coordenadas de los puntos finales del segmento de línea. Es posible que ya se hayan dado. Si no, cuente a lo largo del eje x y el eje y para encontrar las coordenadas.
 .
. y otro en
y otro en  .
.
3. Aplicar las coordenadas a la fórmula de la distancia. Asegúrese de ingresar los valores para las variables correctas. Los dos  -las coordenadas están dentro del primer paréntesis, y los dos
-las coordenadas están dentro del primer paréntesis, y los dos  -las coordenadas están dentro de los siguientes dos corchetes.
-las coordenadas están dentro de los siguientes dos corchetes.
 -las coordenadas están dentro del primer paréntesis, y los dos
-las coordenadas están dentro del primer paréntesis, y los dos  -las coordenadas están dentro de los siguientes dos corchetes.
-las coordenadas están dentro de los siguientes dos corchetes. y
y  , su fórmula se verá así:
, su fórmula se verá así: 
Parte 2 de 2: calcular la distancia

1. Calcular la suma menos entre paréntesis. De acuerdo con el orden de las operaciones, cada cálculo entre paréntesis debe calcularse primero.
- Por ejemplo:

2. Cuadre el valor entre paréntesis. El orden de las operaciones establece que luego tienes que calcular las potencias.



3. Suma los números debajo del signo radical. Puedes hacer este cálculo como si estuvieras trabajando con números enteros.



4. Resolver D  . Para aproximar la respuesta final, encuentra la raíz cuadrada de la suma bajo el radical.
. Para aproximar la respuesta final, encuentra la raíz cuadrada de la suma bajo el radical.
 . Para aproximar la respuesta final, encuentra la raíz cuadrada de la suma bajo el radical.
. Para aproximar la respuesta final, encuentra la raíz cuadrada de la suma bajo el radical.
 unidades.
unidades.Consejos
- No confundas esta fórmula con otras, como la fórmula del punto medio, la fórmula de la pendiente o la ecuación de una recta.
- Tenga en cuenta el orden de las operaciones al calcular la respuesta. Primero resta, luego eleva al cuadrado la diferencia, luego suma y luego calcula la raíz cuadrada.
Artículos sobre el tema. "Cálculo de la longitud de una línea usando la fórmula de la distancia"
Оцените, пожалуйста статью
Popular