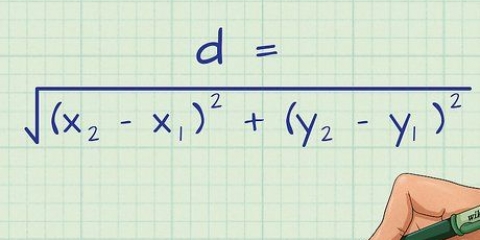Determinar el coeficiente de correlación

Contenido

Pasos
Consejos
Advertencias

El coeficiente de correlación, denotado como r o ρ, es la medida de la correlación lineal (la relación, tanto en fuerza como en dirección) entre dos variables. Va de -1 a +1, utilizando signos de más y menos para representar la correlación positiva y negativa. Si el coeficiente de correlación es exactamente -1, entonces la relación entre las dos variables es completamente negativa; si el coeficiente de correlación es exactamente +1, entonces la relación es completamente positiva. Dos variables pueden tener una correlación positiva, una correlación negativa o ninguna correlación. Puede calcular la correlación a mano, usando algunas calculadoras de correlación gratuitas disponibles en línea o usando las funciones estadísticas de una buena calculadora gráfica.

Pasos

Método 1 de 4: Cálculo manual del coeficiente de correlación

Imagen titulada Encuentra el coeficiente de correlación Paso 1

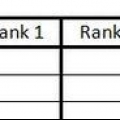
1. Recoge tus datos primero. Para comenzar a calcular una correlación eficiente, primero examine los pares de datos. Es útil para ponerlos en una mesa, tanto en vertical como en horizontal. Etiquete cada fila o columna x e y.

Por ejemplo: suponga que tiene cuatro pares de datos para X y y. Entonces la tabla podría verse así:

x || y
1 || 1
2 || 3
4 || 5
5 || 7

Imagen titulada Encuentra el coeficiente de correlación Paso 2

2. Calcular la media de X. Para calcular la media, debe sumar todos los valores de X sumar y luego dividir por el número de valores.

A partir del ejemplo anterior, observe que tiene cuatro valores para X. Para calcular la media, cuente todos los valores para X y dividirlo por 4. El cálculo entonces se ve así:

m X = (1 + 2 + 4 + 5) / 4

${ estilo de visualización mu _ {x} = (1 + 2 + 4 + 5)/4}$

m X = 12 / 4

${ estilo de visualización mu _ {x} = 12/4}$

m X = 3

${ estilo de visualización mu _ {x} = 3}$

Imagen titulada Encuentra el coeficiente de correlación Paso 3

3. Encuentre la media de y. Para obtener el promedio de y Para encontrarlo, siga los mismos pasos, sumando todos los valores de y y luego dividiendo por el número de valores.

En el ejemplo anterior, también tiene cuatro valores para y. Sume todos estos valores juntos y luego divida por 4. Los cálculos se verán así:

m y = (1 + 3 + 5 + 7) / 4

${ estilo de visualización mu _ {y} = (1 + 3 + 5 + 7)/4}$

m y = dieciséis / 4

${ estilo de visualización mu _ {y} = 16/4}$

m y = 4

${ estilo de visualización mu _ {y} = 4}$

Imagen titulada Encuentra el coeficiente de correlación Paso 4

4. Determine la desviación estándar de X. Una vez que tenga sus medios, puede calcular la desviación estándar. Usa la fórmula para esto:

Σ X = \sqrt{} 1 norte - 1 Σ (X - m_{X})^{2}

${displaystyle sigma _{x}={sqrt {{frac {1}{n-1}}Sigma (x-mu _{x})^{2}}}}$

Con los datos de muestra, sus cálculos se verán así:

Σ X = \sqrt{} 1 4 - 1 * ((1 - 3)^{2} + (2 - 3)^{2} + (4 - 3)^{2} + (5 - 3)^{2})

${displaystyle sigma _{x}={sqrt {{frac {1}{4-1}}*((1-3)^{2}+(2-3)^{2}+(4 -3)^{2}+(5-3)^{2})}}}$

Σ X = \sqrt{} \frac{1}{3} * (4 + 1 + 1 + 4)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(4+1+1+4)}}}$

Σ X = \sqrt{} \frac{1}{3} * (10)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(10)}}}$

Σ X = \sqrt{\frac{10}{3}}

${displaystyle sigma _{x}={sqrt {frac {10}{3}}}}$

Σ X = 1, 83

${ estilo de visualización sigma _ {x} = 1,83}$

Imagen titulada Encuentra el coeficiente de correlación Paso 5

5. Calcular la desviación estándar de y. Usando los mismos pasos básicos, encuentre la desviación estándar de y. Vas a usar la misma fórmula, usando los puntos de datos para y.

Con los datos de muestra, sus cálculos se verán así:

Σ y = \sqrt{} 1 4 - 1 * ((1 - 4)^{2} + (3 - 4)^{2} + (5 - 4)^{2} + (7 - 4)^{2})

${displaystyle sigma _{y}={sqrt {{frac {1}{4-1}}*((1-4)^{2}+(3-4)^{2}+(5 -4)^{2}+(7-4)^{2})}}}$

Σ y = \sqrt{} \frac{1}{3} * (9 + 1 + 1 + 9)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(9+1+1+9)}}}$

Σ y = \sqrt{} \frac{1}{3} * (20)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(20)}}}$

Σ y = \sqrt{\frac{20}{3}}

${displaystyle sigma _{y}={sqrt {frac {20}{3}}}}$

Σ y = 2, 58

${ estilo de visualización sigma _ {y} = 2,58}$

Imagen titulada Encuentra el coeficiente de correlación Paso 6

6. Ver la fórmula básica para determinar un coeficiente de correlación. La fórmula para calcular un coeficiente de correlación utiliza medias, desviaciones estándar y el número de pares en un conjunto de datos (representado por norte). El coeficiente de correlación en sí está representado por la letra minúscula r o la letra griega ρ (rho). Para este artículo, utilizaremos la fórmula conocida como el coeficiente de correlación de Pearson como se muestra a continuación:

ρ = (1 norte - 1) Σ (X - m X Σ_{X}) * (y - m y Σ_{y})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }derecha)*izquierda({frac {y-mu _{y}}{sigma _{y}}}derecha)}$

Puede notar ligeras variaciones en la fórmula, aquí o en otras explicaciones. Por ejemplo, algunos usarán la notación griega con rho y sigma, mientras que otros usarán r y s. Algunas explicaciones pueden usar fórmulas ligeramente diferentes, pero serán matemáticamente equivalentes a esta.

Imagen titulada Encuentra el coeficiente de correlación Paso 7

7. Determinar el coeficiente de correlación. Ahora tiene las medias y las desviaciones estándar de sus variables, por lo que puede pasar a la fórmula del coeficiente de correlación. Recuérdalo norte representa la cantidad de valores que tienes. Ya ha elaborado la otra información relevante en los pasos anteriores.

Usando los datos de muestra, puede ingresar los datos en la fórmula del coeficiente de correlación y calcularlos así:

ρ = (1 norte - 1) Σ (X - m X Σ_{X}) * (y - m y Σ_{y})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }derecha)*izquierda({frac {y-mu _{y}}{sigma _{y}}}derecha)}$

ρ = (\frac{1}{3}) *

${displaystyle rho =left({frac {1}{3}}right)*}$ [

(1 - 3 1, 83) * (1 - 4 2, 58) + (2 - 3 1, 83) * (3 - 4 2, 58)

${displaystyle left({frac {1-3}{1.83}}right)*left({frac {1-4}{2.58}}right)+left({ frac {2- 3}{1.83}}derecha)*izquierda({frac {3-4}{2.58}}derecha)}$

+ (4 - 3 1, 83) * (5 - 4 2, 58) + (5 - 3 1, 83) * (7 - 4 2, 58)

${displaystyle +left({frac {4-3}{1.83}}right)*left({frac {5-4}{2.58}}right)+left({ frac {5 -3}{1,83}}derecha)*izquierda({frac {7-4}{2,58}}derecha)}$ ]

ρ = (\frac{1}{3}) * (6 + 1 + 1 + 6 4, 721)

${displaystyle rho =left({frac {1}{3}}right)*left({frac {6+1+1+6}{4,721}}right)}$

ρ = (\frac{1}{3}) * 2, 965

${displaystyle rho =left({frac {1}{3}}right)*2,965}$

ρ = (2, 965 3)

${displaystyle rho =left({frac {2,965}{3}}right)}$

ρ = 0, 988

${ estilo de visualización rho = 0,988}$

Imagen titulada Encuentra el coeficiente de correlación Paso 8

8. Interpretar el resultado. Para este conjunto de datos, el coeficiente de correlación es 0,988. Este número te dice dos cosas sobre los datos. Mira el signo del número y el tamaño del número.

Dado que el coeficiente de correlación es positivo, puede decir que existe una correlación positiva entre los datos x y los datos y. Esto significa que a medida que aumentan los valores de x, espera que también aumenten los valores de y.

Dado que el coeficiente de correlación está muy cerca de +1, los datos x y los datos y están muy relacionados. Si tuviera que graficar estos puntos, vería que son una muy buena aproximación de una línea recta.

Método 2 de 4: usar calculadoras de correlación en línea

Imagen titulada Encuentra el coeficiente de correlación Paso 9

1. Busque en línea calculadoras de correlación. La medición de la correlación es un cálculo bastante estándar para los estadísticos. El cálculo puede volverse muy tedioso para grandes conjuntos de datos si se hace a mano. Por lo tanto, muchas fuentes han hecho que los cálculos de correlación comunes estén disponibles en línea. Use cualquier motor de búsqueda e ingrese el término de búsqueda `calculadora de correlación`.

Imagen titulada Encuentra el coeficiente de correlación Paso 10

2. Para los datos en. Lea atentamente las instrucciones en el sitio web para que pueda ingresar los datos correctamente. Es importante que los pares de datos se mantengan en orden o obtendrá un resultado de correlación incorrecto. Diferentes sitios web usan diferentes formatos para ingresar datos.

Por ejemplo: en el sitio web http://ncalculadoras.com/estadísticas/correlación-coeficiente-calculadora.htm encuentre un cuadro horizontal para ingresar valores x y un segundo cuadro horizontal para ingresar valores y. Ingresas los términos separados solo por comas. Entonces, el conjunto de datos x calculado anteriormente en este artículo debe ingresarse como 1,2,4,5. El conjunto de datos y se ingresa como 1,3,5,7.

en otro sitio, http://www.alcohol.com/calculators/statistics/correlación-coeficiente/, puede ingresar datos tanto horizontal como verticalmente, siempre y cuando mantenga los puntos de datos en orden.

Imagen titulada Encuentra el coeficiente de correlación Paso 11

3. Calcular los resultados. Estos sitios de cálculo son populares porque, en general, después de ingresar los datos, todo lo que tiene que hacer es hacer clic en el botón `Calcular`; el resultado aparecerá automáticamente.

Método 3 de 4: usar una calculadora gráfica

Imagen titulada Encuentra el coeficiente de correlación Paso 12

1. Introduce tus detalles. En su calculadora gráfica, active la función de estadísticas y luego seleccione el comando `Editar`.

Cada calculadora tiene comandos de teclado ligeramente diferentes. Este artículo proporciona instrucciones específicas para Texas Instruments TI-86.
Ingrese a la función Stat presionando [2nd]-Stat (arriba de la tecla `+`) y luego F2-Edit.

Imagen titulada Encuentra el coeficiente de correlación Paso 13

2. Borrar todos los datos guardados antiguos. La mayoría de las calculadoras mantendrán los datos estadísticos hasta que se borre. Para asegurarse de no confundir datos antiguos con datos nuevos, primero debe borrar toda la información almacenada previamente.

Use las teclas de flecha para mover el cursor para resaltar la categoría `xStat`. Luego presione `Borrar` y `Entrar`. Esto debería borrar todos los valores en la columna xStat.

Use las teclas de flecha para resaltar la categoría `yStat`. Presione `Borrar` y `Entrar` para borrar los datos de esa columna también.

Imagen titulada Encuentra el coeficiente de correlación Paso 14

3. Ingrese los valores de sus datos. Use las teclas de flecha para mover el cursor al primer espacio debajo del encabezado xStat. Escriba su primer valor de datos y luego presione Entrar. Debería ver el espacio en la parte inferior de la pantalla `xStat(1)=__` donde su valor llena el espacio vacío. Cuando presione Entrar, los datos llenarán la tabla, el cursor se moverá a la siguiente línea y la línea en la parte inferior de la pantalla ahora debería leer `xStat(2)=__`.

Continúe ingresando todos los valores de x.

Una vez que haya ingresado los valores de x, use las teclas de flecha para moverse a la columna yStat e ingrese los valores de y.

Cuando se hayan ingresado todos los datos, presione Salir para borrar la pantalla y salir del menú Estadísticas.

Imagen titulada Encuentra el coeficiente de correlación Paso 15

4. Calcular las estadísticas de regresión lineal. El coeficiente de correlación es una medida de qué tan bien los datos se aproximan a una línea recta. Una calculadora gráfica con funciones estadísticas puede calcular muy rápidamente la línea de mejor ajuste y el coeficiente de correlación.

Ingrese a la función Stat y luego presione el botón Calc. En la TI-86 esto es [2nd][Stat][F1].

Elija los cálculos de regresión lineal. En la TI-86, es [F3], con la etiqueta "LinR.` La pantalla gráfica mostrará la línea `LinR _` con un cursor parpadeante.

Ahora necesita ingresar los nombres de las dos variables que desea calcular. Estos son xStat y yStat.

En la TI-86, seleccione la lista de nombres (`Names`) presionando [2nd][List][F3].

La línea inferior de su pantalla ahora debería mostrar las variables disponibles. Elija [xStat] (este es probablemente el botón F1 o F2), luego ingrese una coma y luego [yStat].

Presiona Enter para calcular los datos

Imagen titulada Encuentra el coeficiente de correlación Paso 16

5. Interpretar los resultados. Cuando presione Entrar, la calculadora calculará inmediatamente la siguiente información para los datos que ingresó:

y = a + B X

${ estilo de visualización y = a + bx}$ : Esta es la fórmula general para una línea recta. Sin embargo, en lugar del conocido `y=mx+b`, este se presenta en orden inverso.

a =

${ estilo de visualización a =}$ . Este es el valor de la intersección con el eje y de la línea que mejor se ajusta.

B =

${ estilo de visualización b =}$ . Esta es la pendiente de la línea que mejor se ajusta.

correcto =

${displaystyle {text{corr}}=}$ . Este es el coeficiente de correlación.

norte =

${ estilo de visualización n =}$ . Este es el número de pares de datos utilizados en el cálculo.

Método 4 de 4: repetir lo básico

Imagen titulada Encuentra el coeficiente de correlación Paso 17

1. Comprender el concepto de correlación. La correlación se refiere a la relación estadística entre dos cantidades. El coeficiente de correlación es un número único que puede calcular para dos conjuntos de puntos de datos. El número siempre está entre -1 y +1, e indica qué tan cerca están conectados los dos conjuntos de datos.

Por ejemplo, si mide la altura y la edad de los niños hasta los 12 años, esperaría encontrar una fuerte correlación positiva. A medida que los niños crecen, tienden a ser más altos.
Un ejemplo de una correlación negativa es comparar el tiempo que alguien pasa practicando golf y la puntuación de golf de esa persona. A medida que avanza la práctica, la puntuación debe bajar.
En última instancia, se esperaría poca correlación, positiva o negativa, entre la talla de zapatos de una persona, por ejemplo, y las calificaciones de sus exámenes.

Imagen titulada Encuentra el coeficiente de correlación Paso 18

2. Calcular el promedio. La media aritmética, o "media", de un conjunto de datos se calcula sumando todos los valores de los datos y luego dividiendo por el número de valores en el conjunto. Cuando desee determinar el coeficiente de correlación de sus datos, debe calcular el promedio de cada conjunto de datos.

La media de una variable está indicada por la variable con una línea horizontal encima de ella. Esto a menudo se denomina `barra x` o `barra y` para los conjuntos de datos de x e y. Alternativamente, la media puede ser denotada por la letra griega minúscula μ (mu). Por ejemplo, para representar la media de los puntos de datos de x, podría usar μ_X o µ(x).

Por ejemplo, si tiene un conjunto de x (1,2,5,6,9,10), entonces el promedio de estos datos se calcularía de la siguiente manera:

m X = (1 + 2 + 5 + 6 + 9 + 10) / 6

${ estilo de visualización mu _ {x} = (1+2+5+6+9+10)/6}$

m X = 33 / 6

${ estilo de visualización mu _ {x} = 33/6}$

m X = 5, 5

${ estilo de visualización mu _ {x} = 5,5}$

Imagen titulada Encuentra el coeficiente de correlación Paso 19

3. Conoce la importancia de la desviación estándar. En estadística, la desviación estándar mide la variación y muestra la dispersión de los números en relación con la media. Un grupo de números con una desviación estándar baja están muy cerca unos de otros. Un grupo de números con una desviación estándar alta está más disperso.

Como símbolo, la desviación estándar se expresa con la letra minúscula s o la letra griega σ (sigma). Entonces, la desviación estándar de los datos x se escribe como s_X o_X.

Imagen titulada Encuentra el coeficiente de correlación Paso 20

4. Reconocer la notación de suma. El operador de suma es uno de los operadores más comunes en matemáticas, que representa una suma de valores. Se representa con la letra mayúscula griega, sigma o ∑.

Por ejemplo, si tiene un conjunto de puntos de datos x (1,2,5,6,9,10), entonces ∑x significa:

1+2+5+6+9+10 = 33

Consejos

El coeficiente de correlación a veces se denomina "coeficiente de correlación producto-momento de Pearson", en honor a Karl Pearson, su desarrollador.
En general, un coeficiente de correlación superior a 0,8 (positivo o negativo) representa una fuerte correlación; un coeficiente de correlación inferior a 0,5 (de nuevo positivo o negativo) representa un coeficiente de correlación débil.

Advertencias

La correlación muestra que dos conjuntos de datos están conectados de alguna manera. Sin embargo, tenga cuidado de no interpretar esto como una relación causal. Por ejemplo, si compara las tallas de zapatos de las personas y su altura, es probable que encuentre una fuerte correlación positiva. Las personas más grandes generalmente tienen pies más grandes. Sin embargo, esto no significa que ser alto hará que tus pies crezcan, o que los pies grandes te harán alto. Simplemente suceden juntos.