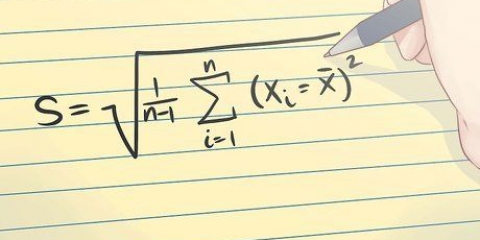Calcular la suma de cuadrados (sse)

Contenido

Pasos

La suma de cuadrados, o SSE, es un cálculo estadístico preliminar que conduce a diferentes valores de datos. Cuando tiene un conjunto de valores de datos, es útil poder determinar qué tan estrechamente se relacionan estos valores entre sí. Tienes que organizar tus datos en una tabla y luego hacer algunos cálculos bastante simples. Una vez que haya encontrado el SSE para un conjunto de datos, puede encontrar la varianza y la desviación estándar.

Pasos

Método 1 de 3: calcular el SSE a mano

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 1

1. Haz una tabla de tres columnas. La forma más fácil de calcular el SSE es comenzar con una tabla de tres columnas. Etiqueta las tres columnas

Donde el

${displaystyle {text{Valor}}}$ ,

desviación

${displaystyle {text{Desviación}}}$ , y

desviación 2

${displaystyle {text{Desviación}}^{2}}$ .

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 2

2. Completa los detalles. La primera columna contiene los valores de sus medidas. Llena la columna

Donde el

${displaystyle {text{Valor}}}$ con tus lecturas. Estos podrían ser los resultados de un experimento, un estudio estadístico o simplemente datos de un problema matemático.

En este caso, suponga que está trabajando con datos médicos y tiene una lista de las temperaturas corporales de diez pacientes. La temperatura corporal normal esperada es de 98.6 grados. Se mide la temperatura de diez pacientes y da los valores 99.0, 98.6, 98.5, 101.1, 98.3, 98.6, 97.9, 98.4, 99.2 y 99.1. Se mide la temperatura de diez pacientes y da los valores 99.0, 98.6, 98.5, 101.1, 98.3, 98.6, 97.9, 98.4, 99.2 y 99.1. Escribe estos valores en la primera columna.

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 3

3. Calcular el promedio. Antes de poder calcular el error de cada medición, debe calcular la media de todo el conjunto de datos.

La media de un conjunto de datos es la suma de sus valores dividida por el número de valores del conjunto. Esto se puede representar simbólicamente, con la variable

m

$mu$ :

m = Σ X norte

${displaystyle mu ={frac {Sigma x}{n}}}$

Para estos datos, el promedio se calcula de la siguiente manera:

m = 99, 0 + 98, 6 + 98, 5 + 101, 1 + 98, 3 + 98, 6 + 97, 9 + 98, 4 + 99, 2 + 99, 1 10

${displaystyle mu ={frac {99,0+98,6+98,5+101,1+98,3+98,6+97,9+98,4+99,2+99,1} {10}}}$

m = 988, 7 10

${displaystyle mu ={frac{988.7}{10}}}$

m = 98, 87

${ estilo de visualización mu = 98,87}$

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 4

4. Calcular los valores de error individuales. En la segunda columna de su tabla, debe ingresar los valores de error para cada valor de datos. El error es la diferencia entre la lectura y la media.

Para el conjunto de datos dado, reste la media, 98,87, de cada valor medido y complete la segunda columna con los resultados. Estos diez cálculos son así:

99, 0 - 98, 87 = 0, 13

${ estilo de visualización 99,0-98,87 = 0,13}$

98, 6 - 98, 87 = - 0, 27

${ estilo de visualización 98,6-98,87 = -0,27}$

98, 5 - 98, 87 = - 0, 37

${ estilo de visualización 98,5-98,87 = -0,37}$

101, 1 - 98, 87 = 2, 23

${ estilo de visualización 101,1-98,87 = 2,23}$

98, 3 - 98, 87 = - 0, 57

${ estilo de visualización 98,3-98,87 = -0,57}$

98, 6 - 98, 87 = - 0, 27

${ estilo de visualización 98,6-98,87 = -0,27}$

97, 9 - 98, 87 = - 0, 97

${ estilo de visualización 97,9-98,87 = -0,97}$

98, 4 - 98, 87 = - 0, 47

${ estilo de visualización 98,4-98,87 = -0,47}$

99, 2 - 98, 87 = 0, 33

${ estilo de visualización 99,2-98,87 = 0,33}$

99, 1 - 98, 87 = 0, 23

${ estilo de visualización 99,1-98,87 = 0,23}$

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 5

5. Calcular el EES. En la tercera columna de la tabla, encuentre el cuadrado de cada uno de los valores resultantes en la columna del medio. Estos representan los cuadrados de la desviación de la media para cada valor de datos medido.

Para cada valor en la columna del medio, use una calculadora para calcular el cuadrado. Registre los resultados en la tercera columna, de la siguiente manera:

0, 13 2 = 0, 0169

${ estilo de visualización 0,13 ^ {2} = 0,0169}$

(- 0, 27) 2 = 0, 0729

${ estilo de visualización (-0,27) ^ {2} = 0,0729}$

(- 0, 37) 2 = 0, 1369

${ estilo de visualización (-0,37) ^ {2} = 0,1369}$

2, 23 2 = 4, 9729

${ estilo de visualización 2,23^{2} = 4,9729}$

(- 0, 57) 2 = 0, 3249

${ estilo de visualización (-0,57) ^ {2} = 0,3249}$

(- 0, 27) 2 = 0, 0729

${ estilo de visualización (-0,27) ^ {2} = 0,0729}$

(- 0, 97) 2 = 0, 9409

${ estilo de visualización (-0,97) ^ {2} = 0,9409}$

(- 0, 47) 2 = 0, 2209

${ estilo de visualización (-0,47) ^ {2} = 0,2209}$

0, 33 2 = 0, 1089

${ estilo de visualización 0,33 ^ {2} = 0,1089}$

0, 23 2 = 0, 0529

${ estilo de visualización 0,23 ^ {2} = 0,0529}$

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 6

6. Sumar los cuadrados de los errores. El último paso es encontrar la suma de los valores en la tercera columna. El resultado deseado es el SSE, o la suma de los cuadrados de los errores.

Para este conjunto de datos, el SSE se calcula sumando los diez valores en la tercera columna:

s s mi = 6, 921

${displaystyle SSE=6.921}$

Método 2 de 3: cree una hoja de cálculo de Excel para calcular el SSE

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 7

1. Etiquetar las columnas de la hoja de cálculo. Crea una tabla con tres columnas en Excel, con los mismos tres encabezados que arriba.

En la celda A1, escriba `Valor` como encabezado.
En el cuadro B1, escriba `Desviación` como encabezado.
En el cuadro C1, escriba `Desviación al cuadrado` como encabezado.

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 8

2. Introduce tus detalles. En la primera columna tienes que introducir los valores de tus medidas. Si el conjunto es pequeño, puede escribirlo fácilmente a mano. Si tiene un conjunto de datos grande, es posible que deba copiar y pegar los datos en la columna.

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 9

3. Determinar el promedio de los puntos de datos. Excel tiene una función que calcula el promedio por ti. En una celda vacía debajo de su tabla de datos (no importa qué celda elija), ingrese:

=Promedio(A2:___)

No escriba espacios vacíos. Complete ese espacio con el nombre de la celda de su último punto de datos. Por ejemplo, si tiene 100 puntos de datos, usaría la función:

=Promedio(A2:A101)

Esta función contiene los datos de las celdas A2 a A101, porque la fila superior contiene los encabezados de columna.

Cuando presiona Enter o hace clic en otra celda de la tabla, la celda recién programada se llena automáticamente con el promedio de sus valores de datos.

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 10

4. Ingrese a la función de medición de error. En la primera celda vacía de la columna "Desviación", debe ingresar una función para calcular la diferencia entre cada punto de datos y la media. Para hacer esto, use el nombre de la celda donde se encuentra la media. Supongamos que has estado usando la celda A104 por ahora.

La función de cálculo de error, que ingresa en la celda B2, es:

=A2-$A$104. Los signos de dólar son necesarios para asegurarse de bloquear la casilla A104 para cada cálculo.

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 11

5. Completa la función para los errores al cuadrado. En la tercera columna puede indicarle a Excel que calcule el cuadrado deseado.

En la celda C2, ingresa la siguiente función:

=B2^2

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 12

6. Copie las funciones para llenar toda la tabla. Después de ingresar las funciones en la celda superior de cada columna, B2 y C2, respectivamente, debe completar toda la tabla. Podría volver a escribir la función en cada línea de la tabla, pero esto llevaría demasiado tiempo. Usando su mouse, resalte las celdas B2 y C2 juntas, y sin soltar el botón del mouse, arrastre a la celda inferior de cada columna.

Suponiendo que tiene 100 puntos de datos en su tabla, arrastre el mouse a las celdas B101 y C101.

Cuando suelta el botón del mouse, las fórmulas se copian en todas las celdas de la tabla. La tabla debe llenarse automáticamente con los valores calculados.

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 13

7. Encuentre el EES. La columna C de su tabla contiene todos los valores de error al cuadrado. El último paso es dejar que Excel calcule la suma de estos valores.

En una celda debajo de la tabla, probablemente C102 en este ejemplo, ingrese la siguiente función:

=Suma(C2:C101)

Al hacer clic en Entrar o al hacer clic en otra celda de la tabla, obtendrá el valor SSE de sus datos.

Método 3 de 3: relacionar SSE con otros datos estadísticos

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 14

1. Calcular la desviación del SSE. Encontrar el SSE para un conjunto de datos es generalmente un bloque de construcción para encontrar otros valores más útiles. El primero de ellos es la varianza. La varianza es una medida que indica cuánto se desvían los datos medidos de la media. En realidad, es la media de las diferencias al cuadrado de la media.

Dado que el SSE es la suma de los errores al cuadrado, puede encontrar la media (esa es la varianza) simplemente dividiendo por el número de valores. Sin embargo, si está calculando la varianza de un conjunto de muestras, en lugar de una población completa, está dividiendo la varianza por (n-1) en lugar de n. Entonces:

Varianza = SSE/n, si calcula la varianza de toda una población.
Varianza = SSE/(n-1), si calcula la varianza de una muestra de datos.

Para el problema de muestra de la temperatura de los pacientes, podemos suponer que 10 pacientes constituyen solo una muestra. Por lo tanto, la varianza se calcula de la siguiente manera:

Diferencia = SSE (norte - 1)

${displaystyle {text{Variación}}={frac {text{SSE}}{(n-1)}}}$

Diferencia = 6, 921 9

${displaystyle {text{Variación}}={frac {6921}{9}}}$

Diferencia = 0, 769

${displaystyle {text{Variación}}=0,769}$

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 15

2. Calcular la desviación estándar del SSE. La desviación estándar es un valor de uso común que indica cuánto se desvían los valores de un conjunto de datos de la media. La desviación estándar es la raíz cuadrada de la varianza. Tenga en cuenta que la varianza es la media de las medidas de error al cuadrado.

Por lo tanto, después de calcular el SSE, puede encontrar la desviación estándar de la siguiente manera:

Desviación Estándar = \sqrt{SSE} norte - 1

${displaystyle {text{Desviación estándar}}={sqrt {frac {text{SSE}}{n-1}}}}$

Para la muestra de las mediciones de temperatura, puede encontrar la desviación estándar de la siguiente manera:

Desviación Estándar = \sqrt{SSE} norte - 1

${displaystyle {text{Desviación estándar}}={sqrt {frac {text{SSE}}{n-1}}}}$

Desviación Estándar = \sqrt{\frac{6.921}{9}}

${displaystyle {text{Desviación estándar}}={sqrt {frac {text{6921}}{9}}}}$

Desviación Estándar = \sqrt{0, 769}

${displaystyle {text{Desviación estándar}}={sqrt {0.769}}}$

Desviación Estándar = 0, 877

${displaystyle {text{Desviación estándar}}=0,877}$

Imagen titulada Calcular la suma de los cuadrados del error (SSE) Paso 16

3. Use SSE para determinar la covarianza. Este artículo se centró en conjuntos de datos que miden solo un valor a la vez. Sin embargo, en muchos estudios puede estar comparando dos valores separados. Por ejemplo, desea saber cómo se relacionan esos dos valores entre sí, no solo con el promedio del conjunto de datos. Este valor es la covarianza.

Los cálculos de la covarianza son demasiado detallados para describirlos aquí, excepto para tener en cuenta que usará el SSE para cada tipo de datos y luego lo comparará. Para obtener una descripción más detallada de la covarianza y los cálculos involucrados, consulte encuentra artículos sobre este tema en wikiHow.

Como ejemplo del uso de la covarianza, podría comparar la edad de los pacientes en un estudio médico con la eficacia de un fármaco para reducir la temperatura febril. Entonces tienes un conjunto de datos de edades y un segundo conjunto de datos de temperaturas. Luego, encuentra el SSE para cada conjunto de datos y, a partir de ahí, la varianza, las desviaciones estándar y la covarianza.