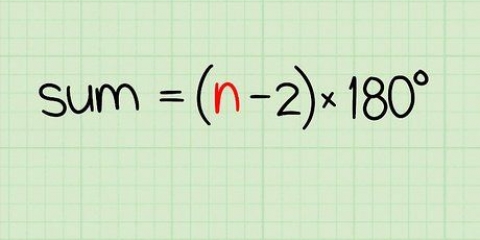Por ejemplo, si desea calcular la suma de la serie 10, 15, 20, 25, 30, entonces  , porque hay cinco números en la secuencia.
, porque hay cinco números en la secuencia. 
Por ejemplo, en la secuencia 10, 15, 20, 25, 30  , y
, y  .
. 

Por ejemplo, si hay cinco números en su secuencia, donde 10 es el primer número y 30 es el último número, su fórmula se verá así:  .
. 
Por ejemplo:



Por ejemplo:


Entonces la suma de la serie (10, 15, 20, 25, 30) es igual a 100. 

Determinar el número de números ( ) en la serie. Como comienzas con tres, terminas con 24 y sumas siete cada vez, la secuencia de números es 3, 10, 17, 24. (El factor de diferencia es la diferencia entre cada número en la serie.) Esto significa que
) en la serie. Como comienzas con tres, terminas con 24 y sumas siete cada vez, la secuencia de números es 3, 10, 17, 24. (El factor de diferencia es la diferencia entre cada número en la serie.) Esto significa que 
Determinar el primero ( ) y última (
) y última ( ) número en la secuencia. Como la secuencia es de 3 a 24,
) número en la secuencia. Como la secuencia es de 3 a 24,  y
y  .
. Encuentre la media de  y
y  :
:  .
. Multiplicar la media por  :
:  .
. 
Determine el número de términos ( ) en la serie. Porque Mara ahorra durante 52 semanas, (1 año),
) en la serie. Porque Mara ahorra durante 52 semanas, (1 año),  .
. Determinar el primero ( ) y última (
) y última ( ) número en la secuencia. La primera cantidad que ahorra son cinco euros, así que
) número en la secuencia. La primera cantidad que ahorra son cinco euros, así que  . Para calcular la cantidad total ahorrada en la última semana del año, calculamos
. Para calcular la cantidad total ahorrada en la última semana del año, calculamos  . entonces
. entonces  .
. Determina la media de  y
y  :
:  .
. Multiplicar la media por  :
:  . Así que ahorró 6890 € al final del año.
. Así que ahorró 6890 € al final del año.
Encontrar la suma de una secuencia aritmética
Contenido
Una secuencia aritmética es una secuencia de números donde cada número aumenta en un valor constante. Para la suma de una secuencia aritmética, puedes sumar todos los números. Sin embargo, esto no es realmente práctico cuando la secuencia contiene una gran cantidad de términos. En su lugar, puede encontrar rápidamente la suma de cada secuencia aritmética multiplicando el promedio del primer y último número por la cantidad de términos en la secuencia.
Pasos
Parte 1 de 3: analizando tu secuencia

1. Asegúrate de tener una secuencia aritmética. Una secuencia aritmética es una lista ordenada de números, donde el cambio de los números es constante. Este método solo funciona si su conjunto de números es una secuencia aritmética.
- Para determinar si se trata de una secuencia aritmética, encuentre la diferencia entre el primer o el último par de números. Asegúrate de que la diferencia sea siempre la misma.
- Por ejemplo, la secuencia de números 10, 15, 20, 25, 30 es una secuencia aritmética, porque la diferencia entre cada número es constantemente cinco.

2. Determine el número de términos en su secuencia. Todo numero es un termino. Si solo se menciona un número, puede contarlos. Si conoce el primer número, el último número y el factor de diferencia (la diferencia entre cada número), puede usar una fórmula para determinar la cantidad de números. Este número es presentado por la variable  .
.
 .
. , porque hay cinco números en la secuencia.
, porque hay cinco números en la secuencia.
3. Encuentra el primer y último número en la secuencia. Necesitas saber ambos números para calcular la suma de la secuencia aritmética. A menudo, el primer número será uno, pero no siempre. Establecer la variable  igual al primer número de la secuencia, y
igual al primer número de la secuencia, y  igual al último número de la secuencia.
igual al último número de la secuencia.
 igual al primer número de la secuencia, y
igual al primer número de la secuencia, y  igual al último número de la secuencia.
igual al último número de la secuencia. , y
, y  .
.Parte 2 de 3: calcular la suma

1. Escribe la fórmula para encontrar la suma de una sucesión aritmética. la fórmula es  , por lo cual
, por lo cual  es igual a la suma de la serie.
es igual a la suma de la serie.
 , por lo cual
, por lo cual  es igual a la suma de la serie.
es igual a la suma de la serie. - Tenga en cuenta que esta fórmula indica que la suma de la secuencia aritmética es igual al promedio del primer y último número multiplicado por el número de números.

2. Introduce los valores norte  ,
, a 1  y
y a norte  en la fórmula en. Asegúrese de sustituir correctamente.
en la fórmula en. Asegúrese de sustituir correctamente.
 ,
,  y
y  en la fórmula en. Asegúrese de sustituir correctamente.
en la fórmula en. Asegúrese de sustituir correctamente. .
.
3. Calcular el promedio del primer y segundo numero. Lo haces sumando los dos números y dividiendo por dos.



4. Multiplica la media por el número de números de la serie. Esto te da la suma de la secuencia aritmética.


Entonces la suma de la serie (10, 15, 20, 25, 30) es igual a 100.
Parte 3 de 3: Completar los problemas de muestra

1. Encuentra la suma de los números del 1 al 500. Incluir todos los enteros consecutivos en el cálculo.
- Determine el número de términos (
) en la serie. Dado que está contando todos los enteros consecutivos hasta el 500 inclusive,
.
- Determinar el primero (
) y última (
) número en la secuencia. Dado que asumimos la serie 1 a 500, se cumple que
y
.
- Encuentre la media de
y
:
.
- Multiplicar la media por
:
.

2. Encuentra la suma de la secuencia aritmética indicada. El primer número en la secuencia es tres. El último número en la secuencia es 24. el factor de diferencia es siete.
 ) en la serie. Como comienzas con tres, terminas con 24 y sumas siete cada vez, la secuencia de números es 3, 10, 17, 24. (El factor de diferencia es la diferencia entre cada número en la serie.) Esto significa que
) en la serie. Como comienzas con tres, terminas con 24 y sumas siete cada vez, la secuencia de números es 3, 10, 17, 24. (El factor de diferencia es la diferencia entre cada número en la serie.) Esto significa que 
 ) y última (
) y última ( ) número en la secuencia. Como la secuencia es de 3 a 24,
) número en la secuencia. Como la secuencia es de 3 a 24,  y
y  .
. y
y  :
:  .
. :
:  .
.
3. Resuelve el siguiente problema. Mara ahorra 5 euros la primera semana del año. El resto del año aumenta sus ahorros en 5 euros cada semana. ¿Cuánto dinero ahorró Mara al final del año??
 ) en la serie. Porque Mara ahorra durante 52 semanas, (1 año),
) en la serie. Porque Mara ahorra durante 52 semanas, (1 año),  .
. ) y última (
) y última ( ) número en la secuencia. La primera cantidad que ahorra son cinco euros, así que
) número en la secuencia. La primera cantidad que ahorra son cinco euros, así que  . Para calcular la cantidad total ahorrada en la última semana del año, calculamos
. Para calcular la cantidad total ahorrada en la última semana del año, calculamos  . entonces
. entonces  .
. y
y  :
:  .
. :
:  . Así que ahorró 6890 € al final del año.
. Así que ahorró 6890 € al final del año.Artículos sobre el tema. "Encontrar la suma de una secuencia aritmética"
Оцените, пожалуйста статью
Similar
Popular