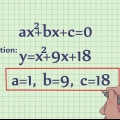Tome la comparación de ejemplo  , donde los términos y se pueden mover hacia la izquierda restando a y de ambos lados. Los otros términos se pueden mover al lado derecho sumando 6 en ambos lados y
, donde los términos y se pueden mover hacia la izquierda restando a y de ambos lados. Los otros términos se pueden mover al lado derecho sumando 6 en ambos lados y  sacar de ambos lados. La ecuación resultante es
sacar de ambos lados. La ecuación resultante es  .
. 
Ver la comparación de ejemplo  . No hay limitación en los valores permitidos de x para esta ecuación. Sin embargo, debes darte cuenta de que esta es la ecuación de una parábola, con x=0 como su centro, y una parábola no es una función porque no es una comparación uno a uno de los valores de x e y. Para limitar esta ecuación y convertirla en una función, para la cual podemos encontrar una inversa, necesitamos definir el dominio como x≥0.
. No hay limitación en los valores permitidos de x para esta ecuación. Sin embargo, debes darte cuenta de que esta es la ecuación de una parábola, con x=0 como su centro, y una parábola no es una función porque no es una comparación uno a uno de los valores de x e y. Para limitar esta ecuación y convertirla en una función, para la cual podemos encontrar una inversa, necesitamos definir el dominio como x≥0. El rango está limitado de la misma manera. Nótese que el primer término,  , siempre será positivo o 0, para cualquier valor de x. Entonces si la ecuación suma +2, el rango será cualquier valor y≥2.
, siempre será positivo o 0, para cualquier valor de x. Entonces si la ecuación suma +2, el rango será cualquier valor y≥2. Es necesario definir el dominio y el alcance en esta etapa temprana. Usará estas definiciones más adelante cuando defina el dominio y el alcance de la función inversa. De hecho, el dominio de la función original se convierte en el rango de la función inversa, y el rango de la función original se convierte en el dominio de la función inversa. 
Trabajando con la comparación de ejemplo  , este paso de inversión dará como resultado la nueva ecuación de
, este paso de inversión dará como resultado la nueva ecuación de  .
. Un formato alternativo es reemplazar los términos y con x, pero reemplazar los términos x con  o
o  para indicar la función inversa.
para indicar la función inversa. 
 (premisa original)
(premisa original) (restar 2 de ambos lados)
(restar 2 de ambos lados) (dividir ambos lados por 2)
(dividir ambos lados por 2)± (raíz cuadrada de ambos lados; recuerda que la raíz cuadrada da como resultado posibles respuestas tanto positivas como negativas)
(raíz cuadrada de ambos lados; recuerda que la raíz cuadrada da como resultado posibles respuestas tanto positivas como negativas) 
Ver la solución de la ecuación de ejemplo ± . Dado que la función raíz cuadrada no está definida para valores negativos, el término debe ser
. Dado que la función raíz cuadrada no está definida para valores negativos, el término debe ser  siempre se positivo. Por lo tanto, los valores permitidos de x (el dominio) deben ser x≥2. Con eso como dominio, los valores resultantes de y (el rango) son todos valores y≥0, si toma la solución positiva de la raíz cuadrada, o y≤0, si toma la solución negativa de la raíz cuadrada. Tenga en cuenta que para encontrar la función inversa, originalmente definió el dominio como x≥0. Por lo tanto, la solución correcta para la función inversa es la opción positiva.
siempre se positivo. Por lo tanto, los valores permitidos de x (el dominio) deben ser x≥2. Con eso como dominio, los valores resultantes de y (el rango) son todos valores y≥0, si toma la solución positiva de la raíz cuadrada, o y≤0, si toma la solución negativa de la raíz cuadrada. Tenga en cuenta que para encontrar la función inversa, originalmente definió el dominio como x≥0. Por lo tanto, la solución correcta para la función inversa es la opción positiva. Compara el dominio y rango del inverso con el dominio y rango del original. Recuerda que para la función original,  , el dominio se definió como todos los valores de x≥0, y el rango se definió como todos los valores de y≥2. Para la función inversa, ahora estos valores se intercambian, y el dominio son todos los valores de x≥2, y el rango son todos los valores de y≥0.
, el dominio se definió como todos los valores de x≥0, y el rango se definió como todos los valores de y≥2. Para la función inversa, ahora estos valores se intercambian, y el dominio son todos los valores de x≥2, y el rango son todos los valores de y≥0. 
Como ejemplo, elija el valor x=1 para la ecuación original  . Esto da el resultado y=4.
. Esto da el resultado y=4. Luego pones el valor 4 en la función inversa  . Esto de hecho da el resultado y=1. Puedes concluir que tu función inversa es correcta.
. Esto de hecho da el resultado y=1. Puedes concluir que tu función inversa es correcta. 

Tenga en cuenta que esta forma estándar consiste en un término cuadrático perfecto,  , que luego se modifica por los otros dos elementos a y k. Para llegar a esta forma cuadrática perfecta, deberá crear ciertas condiciones en su ecuación cuadrática.
, que luego se modifica por los otros dos elementos a y k. Para llegar a esta forma cuadrática perfecta, deberá crear ciertas condiciones en su ecuación cuadrática. 
Para completar el cuadrado, trabajar en sentido inverso. empiezas con  y un segundo término x. Del coeficiente de ese término, que puedes definir como `2b`, debes obtener
y un segundo término x. Del coeficiente de ese término, que puedes definir como `2b`, debes obtener  ver para encontrar. Esto requiere una combinación de dividir por dos y luego elevar al cuadrado ese resultado.
ver para encontrar. Esto requiere una combinación de dividir por dos y luego elevar al cuadrado ese resultado. 
Tomemos, por ejemplo, la función cuadrática  . Puedes simplificar esto dividiendo todos los términos por 2 para obtener la función resultante
. Puedes simplificar esto dividiendo todos los términos por 2 para obtener la función resultante  Llegar. El coeficiente 2 permanece fuera de los corchetes y será parte de su solución final.
Llegar. El coeficiente 2 permanece fuera de los corchetes y será parte de su solución final. Si todos los términos no son múltiplos de a, obtienes coeficientes fraccionarios. Por ejemplo: la función  se simplificará a
se simplificará a  . Calcula las fracciones con cuidado.
. Calcula las fracciones con cuidado. 
Por ejemplo, si los primeros dos términos de tu función cuadrática  encuentras el tercer término necesario dividiendo 3 por 2 (o 3/2), y luego elevándolo al cuadrado, para obtener 9/4. el cuadrático
encuentras el tercer término necesario dividiendo 3 por 2 (o 3/2), y luego elevándolo al cuadrado, para obtener 9/4. el cuadrático  es un cuadrado perfecto.
es un cuadrado perfecto. Otro ejemplo: supongamos que los dos primeros términos  son. La mitad del término medio es -2, y luego lo elevas al cuadrado para obtener 4. El cuadrado perfecto resultante es
son. La mitad del término medio es -2, y luego lo elevas al cuadrado para obtener 4. El cuadrado perfecto resultante es  .
. 
Supongamos que tiene la función  . Como se mencionó anteriormente, usa los primeros dos términos para completar el cuadrado. Usando el término medio de -4x, generas un tercer término +4. Suma 4 y resta 4 de la ecuación, en la forma
. Como se mencionó anteriormente, usa los primeros dos términos para completar el cuadrado. Usando el término medio de -4x, generas un tercer término +4. Suma 4 y resta 4 de la ecuación, en la forma  . Los paréntesis solo se colocan para definir la ecuación cuadrática que estás haciendo. Tenga en cuenta el +4 dentro de los corchetes y el -4 en el exterior. Simplifica los números al resultado
. Los paréntesis solo se colocan para definir la ecuación cuadrática que estás haciendo. Tenga en cuenta el +4 dentro de los corchetes y el -4 en el exterior. Simplifica los números al resultado  .
. 
Tenga en cuenta que para esta función a=1, h=2 y k=5. El valor de escribir la ecuación de esta forma es que a, porque es positiva, te dice que la parábola está apuntando hacia arriba. Los valores (h, k) indican el vértice en la parte inferior de la parábola, si quisieras graficarla. 
Continuar trabajando con la función de vista previa  . Como esto está en formato estándar, puede determinar el vértice como x=2, y=5. Entonces, para evitar la simetría, solo trabaja con el lado derecho del gráfico y establece el dominio si todos los valores x≥2. Insertar el valor x=2 en la función devuelve y=5. Puedes ver que los valores de y aumentarán a medida que x aumenta. Por lo tanto, el rango de esta ecuación es y≥5.
. Como esto está en formato estándar, puede determinar el vértice como x=2, y=5. Entonces, para evitar la simetría, solo trabaja con el lado derecho del gráfico y establece el dominio si todos los valores x≥2. Insertar el valor x=2 en la función devuelve y=5. Puedes ver que los valores de y aumentarán a medida que x aumenta. Por lo tanto, el rango de esta ecuación es y≥5. 
Continuar trabajando con la función  . Inserte x en lugar de f(x) e inserte y (o f(x), si lo prefiere) en lugar de x. Esto da como una nueva función
. Inserte x en lugar de f(x) e inserte y (o f(x), si lo prefiere) en lugar de x. Esto da como una nueva función  .
. 
 (punto de partida inicial)
(punto de partida inicial) (restar 5 de ambos lados)
(restar 5 de ambos lados)± (raíz cuadrada de ambos lados; recuerde que la raíz cuadrada produce respuestas posibles tanto positivas como negativas)
(raíz cuadrada de ambos lados; recuerde que la raíz cuadrada produce respuestas posibles tanto positivas como negativas) ± (suma 2 a ambos lados)
(suma 2 a ambos lados) 
Ver la solución de la ecuación de ejemplo ± . Dado que la función raíz cuadrada no está definida para valores negativos, el término debe ser
. Dado que la función raíz cuadrada no está definida para valores negativos, el término debe ser  siempre se positivo. Por lo tanto, los valores permitidos de x (el dominio) deben ser x≥5. Con eso como dominio, los valores resultantes de y (el rango) son todos los valores y≥2 (si toma la solución positiva de la raíz cuadrada), o y≤2 (si elige la solución negativa de la raíz cuadrada). Recuerda que originalmente definiste el dominio como x≥2, para encontrar la función inversa. Por lo tanto, la solución correcta para la función inversa es la opción positiva.
siempre se positivo. Por lo tanto, los valores permitidos de x (el dominio) deben ser x≥5. Con eso como dominio, los valores resultantes de y (el rango) son todos los valores y≥2 (si toma la solución positiva de la raíz cuadrada), o y≤2 (si elige la solución negativa de la raíz cuadrada). Recuerda que originalmente definiste el dominio como x≥2, para encontrar la función inversa. Por lo tanto, la solución correcta para la función inversa es la opción positiva. Compara el dominio y rango del inverso con el dominio y rango del original. Recuerde que para la función original, el dominio se definió como todos los valores de x≥2, y el rango se definió como todos los valores de y≥5. Para esta función inversa estos valores se intercambian, y el dominio ahora son todos los valores de x≥5, y el rango son todos los valores de y≥2. 
Como ejemplo, elija el valor x=3 para incluir en la ecuación original  procesar. Esto da el resultado y=6.
procesar. Esto da el resultado y=6. Luego procesas y=6 en la función inversa  . Esto devuelve y=3, que es el número con el que comenzaste. Puedes concluir que tu función inversa es correcta.
. Esto devuelve y=3, que es el número con el que comenzaste. Puedes concluir que tu función inversa es correcta. 

Para esta sección de este artículo, utilizará la ecuación de muestra  .
. 

Basado en la ecuación del trabajo  , esto da el resultado
, esto da el resultado  .
. 
Para la ecuación de ejemplo, para que el lado izquierdo sea igual a cero, debe restar x de ambos lados de la ecuación. Esto da el resultado  .
. 
Salir  . Entonces, x=1
. Entonces, x=1 Salir  . Entonces, b=2
. Entonces, b=2 Salir  . Entonces, c=(-3-x)
. Entonces, c=(-3-x) 
x=[-b±√(b^2-4ac)]/2a x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1) x=((-2)±√(4+12+4x)))/2 x=(-2±√(16+4x))/2 x=(-2±√(4)(4+x)))/2 x=-2±2√(4+x))/2 x=-1±√(4+x) f-inverse = -1±√(4+x)(Este último paso es posible porque cambiaste f(x) por la variable x en una etapa anterior). 




Asumiendo la función original  , elige tu x=-2. Esto devuelve y=-3. Ahora sustituya el valor de x=-3 en la función inversa,
, elige tu x=-2. Esto devuelve y=-3. Ahora sustituya el valor de x=-3 en la función inversa,  . Esto devuelve -2, que de hecho es el valor con el que comenzaste. Entonces tu definición de la función inversa es correcta.
. Esto devuelve -2, que de hecho es el valor con el que comenzaste. Entonces tu definición de la función inversa es correcta.
Encontrar el inverso de una ecuación cuadrática
Contenido
Las funciones inversas pueden ser muy útiles para resolver muchos problemas matemáticos. Ser capaz de tomar una función y encontrar su función inversa es una herramienta poderosa. Sin embargo, con ecuaciones cuadráticas, esto puede ser un proceso bastante complicado. Primero debe definir cuidadosamente la ecuación, determinando un dominio y un rango apropiados. A continuación, tiene la opción de tres métodos para calcular la función inversa. La elección del método es principalmente una cuestión de preferencia personal.
Pasos
Método 1 de 3: Encontrar el inverso de una función simple

1. Encuentre una función en la forma de y = a X 2 + C  . Si tiene el tipo de función `correcto` para empezar, puede encontrar el inverso con un poco de álgebra simple. Esta forma es una especie de variación de
. Si tiene el tipo de función `correcto` para empezar, puede encontrar el inverso con un poco de álgebra simple. Esta forma es una especie de variación de  . Si comparas esto con una función cuadrática estándar,
. Si comparas esto con una función cuadrática estándar,  , ver que el termino medio
, ver que el termino medio  Está perdido. Otra forma de decir esto es que el valor de b es cero. Si tu función tiene esta forma, encontrar la inversa es bastante fácil.
Está perdido. Otra forma de decir esto es que el valor de b es cero. Si tu función tiene esta forma, encontrar la inversa es bastante fácil.
 . Si tiene el tipo de función `correcto` para empezar, puede encontrar el inverso con un poco de álgebra simple. Esta forma es una especie de variación de
. Si tiene el tipo de función `correcto` para empezar, puede encontrar el inverso con un poco de álgebra simple. Esta forma es una especie de variación de  . Si comparas esto con una función cuadrática estándar,
. Si comparas esto con una función cuadrática estándar,  , ver que el termino medio
, ver que el termino medio  Está perdido. Otra forma de decir esto es que el valor de b es cero. Si tu función tiene esta forma, encontrar la inversa es bastante fácil.
Está perdido. Otra forma de decir esto es que el valor de b es cero. Si tu función tiene esta forma, encontrar la inversa es bastante fácil. - Su función inicial no tiene que verse exactamente como
. Siempre que pueda mirarlo y ver que la función solo consiste en
términos y números constantes, podrá utilizar este método.
- Supongamos que empiezas con la ecuación
. Un examen rápido de esta ecuación revela que no hay términos de
ser a la primera potencia. Esta ecuación es candidata para este método para encontrar una función inversa.

2. Simplifica combinando términos semejantes. La ecuación inicial puede tener múltiples términos en una combinación de suma y resta. Su primer paso es combinar términos similares para simplificar la ecuación y reescribirla en el formato estándar  .
.
 .
. , donde los términos y se pueden mover hacia la izquierda restando a y de ambos lados. Los otros términos se pueden mover al lado derecho sumando 6 en ambos lados y
, donde los términos y se pueden mover hacia la izquierda restando a y de ambos lados. Los otros términos se pueden mover al lado derecho sumando 6 en ambos lados y  sacar de ambos lados. La ecuación resultante es
sacar de ambos lados. La ecuación resultante es  .
.
3. Determinar el dominio y rango de la función simplificada. Recuerda que el dominio de una función está formado por los posibles valores de x que se pueden aplicar para dar una solución real. El rango de una función está formado por los valores de y que devolverá. Para determinar el dominio de la función, busca valores que produzcan un resultado matemáticamente imposible. Luego indica el dominio si todos los demás valores de x. Para encontrar el rango, considere los valores de y en puntos límite arbitrarios y observe el comportamiento de la función.
 . No hay limitación en los valores permitidos de x para esta ecuación. Sin embargo, debes darte cuenta de que esta es la ecuación de una parábola, con x=0 como su centro, y una parábola no es una función porque no es una comparación uno a uno de los valores de x e y. Para limitar esta ecuación y convertirla en una función, para la cual podemos encontrar una inversa, necesitamos definir el dominio como x≥0.
. No hay limitación en los valores permitidos de x para esta ecuación. Sin embargo, debes darte cuenta de que esta es la ecuación de una parábola, con x=0 como su centro, y una parábola no es una función porque no es una comparación uno a uno de los valores de x e y. Para limitar esta ecuación y convertirla en una función, para la cual podemos encontrar una inversa, necesitamos definir el dominio como x≥0. , siempre será positivo o 0, para cualquier valor de x. Entonces si la ecuación suma +2, el rango será cualquier valor y≥2.
, siempre será positivo o 0, para cualquier valor de x. Entonces si la ecuación suma +2, el rango será cualquier valor y≥2.
4. Intercambiar los roles de los términos x e y. Sin cambiar la ecuación de ninguna otra manera, debe reemplazar todas las formas de y con x, y todas las formas de x con y. Este es el paso que realmente `invierte` la ecuación.
 , este paso de inversión dará como resultado la nueva ecuación de
, este paso de inversión dará como resultado la nueva ecuación de  .
. o
o  para indicar la función inversa.
para indicar la función inversa.
5. Reescribe la ecuación inversa en términos de y. Usando una combinación de pasos algebraicos y asegurándose de que se realice la misma operación en ambos lados de la ecuación, deberá aislar la variable y. para la comparacion  , esta revisión se ve así:
, esta revisión se ve así:
 , esta revisión se ve así:
, esta revisión se ve así: (premisa original)
(premisa original) (restar 2 de ambos lados)
(restar 2 de ambos lados) (dividir ambos lados por 2)
(dividir ambos lados por 2) (raíz cuadrada de ambos lados; recuerda que la raíz cuadrada da como resultado posibles respuestas tanto positivas como negativas)
(raíz cuadrada de ambos lados; recuerda que la raíz cuadrada da como resultado posibles respuestas tanto positivas como negativas)
6. Determinar el dominio y el rango de la función inversa. Como al principio, examina la ecuación invertida para determinar el dominio y el rango. Con dos soluciones posibles, elija la solución que tenga un dominio y un rango que sean los inversos del dominio y el rango originales.
 . Dado que la función raíz cuadrada no está definida para valores negativos, el término debe ser
. Dado que la función raíz cuadrada no está definida para valores negativos, el término debe ser  siempre se positivo. Por lo tanto, los valores permitidos de x (el dominio) deben ser x≥2. Con eso como dominio, los valores resultantes de y (el rango) son todos valores y≥0, si toma la solución positiva de la raíz cuadrada, o y≤0, si toma la solución negativa de la raíz cuadrada. Tenga en cuenta que para encontrar la función inversa, originalmente definió el dominio como x≥0. Por lo tanto, la solución correcta para la función inversa es la opción positiva.
siempre se positivo. Por lo tanto, los valores permitidos de x (el dominio) deben ser x≥2. Con eso como dominio, los valores resultantes de y (el rango) son todos valores y≥0, si toma la solución positiva de la raíz cuadrada, o y≤0, si toma la solución negativa de la raíz cuadrada. Tenga en cuenta que para encontrar la función inversa, originalmente definió el dominio como x≥0. Por lo tanto, la solución correcta para la función inversa es la opción positiva. , el dominio se definió como todos los valores de x≥0, y el rango se definió como todos los valores de y≥2. Para la función inversa, ahora estos valores se intercambian, y el dominio son todos los valores de x≥2, y el rango son todos los valores de y≥0.
, el dominio se definió como todos los valores de x≥0, y el rango se definió como todos los valores de y≥2. Para la función inversa, ahora estos valores se intercambian, y el dominio son todos los valores de x≥2, y el rango son todos los valores de y≥0.
7. Comprueba si tu función inversa funciona. Para asegurarse de que su trabajo sea correcto y que su inversa sea la ecuación correcta, elija cualquier valor para x y colóquelo en la ecuación original para encontrar y. Luego coloca ese valor de y en el lugar de x en tu ecuación inversa, y mira si obtienes el número con el que comenzaste. Si es así, tu función inversa es correcta.
 . Esto da el resultado y=4.
. Esto da el resultado y=4. . Esto de hecho da el resultado y=1. Puedes concluir que tu función inversa es correcta.
. Esto de hecho da el resultado y=1. Puedes concluir que tu función inversa es correcta.Método 2 de 3: Completar el cuadrado para encontrar la función inversa

1. Dar a la ecuación cuadrática la forma correcta. Para encontrar la inversa, tienes que empezar con la ecuación de la forma  . Si es necesario, debe combinar términos similares para obtener la ecuación en este formato. Con la ecuación escrita de esta manera, puedes contar un poco más al respecto.
. Si es necesario, debe combinar términos similares para obtener la ecuación en este formato. Con la ecuación escrita de esta manera, puedes contar un poco más al respecto.
 . Si es necesario, debe combinar términos similares para obtener la ecuación en este formato. Con la ecuación escrita de esta manera, puedes contar un poco más al respecto.
. Si es necesario, debe combinar términos similares para obtener la ecuación en este formato. Con la ecuación escrita de esta manera, puedes contar un poco más al respecto. - Lo primero que notará es el valor del coeficiente a. si un>0, entonces la ecuación define una parábola cuyos extremos apuntan hacia arriba (parábola de valle). si un<0, entonces la ecuación define una parábola cuyos extremos apuntan hacia abajo (parábola de montaña). Tenga en cuenta que a≠0. Si no fuera así, sería una función lineal y no cuadrática.

2. Reconocer el formato estándar de la cuadrática. Antes de que puedas encontrar la función inversa, debes reescribir la ecuación en el formato estándar. El formato estándar para una función cuadrática es  . Los términos numéricos a, h y k se evaluarán si transforma la ecuación calculando el cuadrado.
. Los términos numéricos a, h y k se evaluarán si transforma la ecuación calculando el cuadrado.
 . Los términos numéricos a, h y k se evaluarán si transforma la ecuación calculando el cuadrado.
. Los términos numéricos a, h y k se evaluarán si transforma la ecuación calculando el cuadrado. , que luego se modifica por los otros dos elementos a y k. Para llegar a esta forma cuadrática perfecta, deberá crear ciertas condiciones en su ecuación cuadrática.
, que luego se modifica por los otros dos elementos a y k. Para llegar a esta forma cuadrática perfecta, deberá crear ciertas condiciones en su ecuación cuadrática.
3. Piensa en la forma de una función cuadrática perfecta. Recuerda que una función cuadrática que es un cuadrado perfecto surge de dos binomios de  , o
, o  . Si haces esta multiplicación, obtienes
. Si haces esta multiplicación, obtienes  . Así que el primer término de la cuadrática es el primer término de la binomio, elevado al cuadrado, y el último término de la cuadrática es el cuadrado del segundo término de la binomio. El término medio consiste en el doble del producto de los dos términos, en este caso
. Así que el primer término de la cuadrática es el primer término de la binomio, elevado al cuadrado, y el último término de la cuadrática es el cuadrado del segundo término de la binomio. El término medio consiste en el doble del producto de los dos términos, en este caso  .
.
 , o
, o  . Si haces esta multiplicación, obtienes
. Si haces esta multiplicación, obtienes  . Así que el primer término de la cuadrática es el primer término de la binomio, elevado al cuadrado, y el último término de la cuadrática es el cuadrado del segundo término de la binomio. El término medio consiste en el doble del producto de los dos términos, en este caso
. Así que el primer término de la cuadrática es el primer término de la binomio, elevado al cuadrado, y el último término de la cuadrática es el cuadrado del segundo término de la binomio. El término medio consiste en el doble del producto de los dos términos, en este caso  .
. y un segundo término x. Del coeficiente de ese término, que puedes definir como `2b`, debes obtener
y un segundo término x. Del coeficiente de ese término, que puedes definir como `2b`, debes obtener  ver para encontrar. Esto requiere una combinación de dividir por dos y luego elevar al cuadrado ese resultado.
ver para encontrar. Esto requiere una combinación de dividir por dos y luego elevar al cuadrado ese resultado.
4. Asegúrese de que el coeficiente de X 2  1 es. ¿Recuerdas la forma original de la función cuadrática?
1 es. ¿Recuerdas la forma original de la función cuadrática?  . Si el primer coeficiente es distinto de 1, entonces debe dividir todos los términos por ese valor para obtener a = 1.
. Si el primer coeficiente es distinto de 1, entonces debe dividir todos los términos por ese valor para obtener a = 1.
 1 es. ¿Recuerdas la forma original de la función cuadrática?
1 es. ¿Recuerdas la forma original de la función cuadrática?  . Si el primer coeficiente es distinto de 1, entonces debe dividir todos los términos por ese valor para obtener a = 1.
. Si el primer coeficiente es distinto de 1, entonces debe dividir todos los términos por ese valor para obtener a = 1. . Puedes simplificar esto dividiendo todos los términos por 2 para obtener la función resultante
. Puedes simplificar esto dividiendo todos los términos por 2 para obtener la función resultante  Llegar. El coeficiente 2 permanece fuera de los corchetes y será parte de su solución final.
Llegar. El coeficiente 2 permanece fuera de los corchetes y será parte de su solución final. se simplificará a
se simplificará a  . Calcula las fracciones con cuidado.
. Calcula las fracciones con cuidado.
5. Encuentra la mitad del coeficiente del medio y elevalo al cuadrado. Ya tienes los dos primeros términos de la fórmula cuadrática. Estos son el término  y el coeficiente que representa el término x. Tomando ese coeficiente como el valor que tiene, puedes sumar o restar el número necesario para hacer un cuadrado perfecto. Recuerde de arriba que el tercer término requerido del cuadrado es este segundo coeficiente dividido por dos, y luego elevado al cuadrado.
y el coeficiente que representa el término x. Tomando ese coeficiente como el valor que tiene, puedes sumar o restar el número necesario para hacer un cuadrado perfecto. Recuerde de arriba que el tercer término requerido del cuadrado es este segundo coeficiente dividido por dos, y luego elevado al cuadrado.
 y el coeficiente que representa el término x. Tomando ese coeficiente como el valor que tiene, puedes sumar o restar el número necesario para hacer un cuadrado perfecto. Recuerde de arriba que el tercer término requerido del cuadrado es este segundo coeficiente dividido por dos, y luego elevado al cuadrado.
y el coeficiente que representa el término x. Tomando ese coeficiente como el valor que tiene, puedes sumar o restar el número necesario para hacer un cuadrado perfecto. Recuerde de arriba que el tercer término requerido del cuadrado es este segundo coeficiente dividido por dos, y luego elevado al cuadrado. encuentras el tercer término necesario dividiendo 3 por 2 (o 3/2), y luego elevándolo al cuadrado, para obtener 9/4. el cuadrático
encuentras el tercer término necesario dividiendo 3 por 2 (o 3/2), y luego elevándolo al cuadrado, para obtener 9/4. el cuadrático  es un cuadrado perfecto.
es un cuadrado perfecto. son. La mitad del término medio es -2, y luego lo elevas al cuadrado para obtener 4. El cuadrado perfecto resultante es
son. La mitad del término medio es -2, y luego lo elevas al cuadrado para obtener 4. El cuadrado perfecto resultante es  .
.
6. Suma y resta del tercer término requerido al mismo tiempo. Este es un concepto complicado, pero funciona. Sumar y restar el mismo número en diferentes lugares de su función realmente no cambia el valor de la función. Sin embargo, al hacer esto, obtendrá su función en la forma adecuada.
 . Como se mencionó anteriormente, usa los primeros dos términos para completar el cuadrado. Usando el término medio de -4x, generas un tercer término +4. Suma 4 y resta 4 de la ecuación, en la forma
. Como se mencionó anteriormente, usa los primeros dos términos para completar el cuadrado. Usando el término medio de -4x, generas un tercer término +4. Suma 4 y resta 4 de la ecuación, en la forma  . Los paréntesis solo se colocan para definir la ecuación cuadrática que estás haciendo. Tenga en cuenta el +4 dentro de los corchetes y el -4 en el exterior. Simplifica los números al resultado
. Los paréntesis solo se colocan para definir la ecuación cuadrática que estás haciendo. Tenga en cuenta el +4 dentro de los corchetes y el -4 en el exterior. Simplifica los números al resultado  .
.
7. Factorizar la ecuación cuadrática. El polinomio entre paréntesis es una ecuación cuadrática, que puedes reescribir como  . En el ejemplo del paso anterior (
. En el ejemplo del paso anterior ( ) se factoriza el factor cuadrático en
) se factoriza el factor cuadrático en  . Copia el resto de la ecuación para que tu solución
. Copia el resto de la ecuación para que tu solución  se está convirtiendo. Esta es la misma función que su ecuación cuadrática original (
se está convirtiendo. Esta es la misma función que su ecuación cuadrática original ( ), reescrito como la forma estándar
), reescrito como la forma estándar  .
.
 . En el ejemplo del paso anterior (
. En el ejemplo del paso anterior ( ) se factoriza el factor cuadrático en
) se factoriza el factor cuadrático en  . Copia el resto de la ecuación para que tu solución
. Copia el resto de la ecuación para que tu solución  se está convirtiendo. Esta es la misma función que su ecuación cuadrática original (
se está convirtiendo. Esta es la misma función que su ecuación cuadrática original ( ), reescrito como la forma estándar
), reescrito como la forma estándar  .
.
8. Definir el dominio y alcance de la función. El dominio es el conjunto de valores de x que se pueden usar como entradas a la función. El rango es el conjunto de valores de y que puede ser el resultado. Recuerda que una parábola no es una función con una inversa definible, porque no existe una relación de uno a uno entre los valores de x y los valores de y, debido a la simetría de la parábola. Para resolver este problema, debes definir el dominio como todos los valores de x que son mayores que x=h, el vértice de la parábola.
 . Como esto está en formato estándar, puede determinar el vértice como x=2, y=5. Entonces, para evitar la simetría, solo trabaja con el lado derecho del gráfico y establece el dominio si todos los valores x≥2. Insertar el valor x=2 en la función devuelve y=5. Puedes ver que los valores de y aumentarán a medida que x aumenta. Por lo tanto, el rango de esta ecuación es y≥5.
. Como esto está en formato estándar, puede determinar el vértice como x=2, y=5. Entonces, para evitar la simetría, solo trabaja con el lado derecho del gráfico y establece el dominio si todos los valores x≥2. Insertar el valor x=2 en la función devuelve y=5. Puedes ver que los valores de y aumentarán a medida que x aumenta. Por lo tanto, el rango de esta ecuación es y≥5.
9. Intercambiar los valores de x e y. Este es el paso donde comienzas por encontrar la forma inversa de la ecuación. Deje la ecuación en su totalidad excepto el intercambio de estas variables.
 . Inserte x en lugar de f(x) e inserte y (o f(x), si lo prefiere) en lugar de x. Esto da como una nueva función
. Inserte x en lugar de f(x) e inserte y (o f(x), si lo prefiere) en lugar de x. Esto da como una nueva función  .
.
10. Reescribe la ecuación inversa en términos de y. Usando una combinación de pasos algebraicos, asegurándose de realizar la misma operación de manera uniforme en ambos lados de la ecuación, aísle la variable y. Para la comparación de trabajo  esta revisión se ve así:
esta revisión se ve así:
 esta revisión se ve así:
esta revisión se ve así: (punto de partida inicial)
(punto de partida inicial) (restar 5 de ambos lados)
(restar 5 de ambos lados) (raíz cuadrada de ambos lados; recuerde que la raíz cuadrada produce respuestas posibles tanto positivas como negativas)
(raíz cuadrada de ambos lados; recuerde que la raíz cuadrada produce respuestas posibles tanto positivas como negativas) (suma 2 a ambos lados)
(suma 2 a ambos lados)
11. Determinar el dominio y el rango de la función inversa. Como al principio, examina la ecuación inversa para determinar el dominio y el rango. Con dos soluciones posibles, elija la solución que tenga un dominio y un rango que sean los inversos del dominio y el rango originales.
 . Dado que la función raíz cuadrada no está definida para valores negativos, el término debe ser
. Dado que la función raíz cuadrada no está definida para valores negativos, el término debe ser  siempre se positivo. Por lo tanto, los valores permitidos de x (el dominio) deben ser x≥5. Con eso como dominio, los valores resultantes de y (el rango) son todos los valores y≥2 (si toma la solución positiva de la raíz cuadrada), o y≤2 (si elige la solución negativa de la raíz cuadrada). Recuerda que originalmente definiste el dominio como x≥2, para encontrar la función inversa. Por lo tanto, la solución correcta para la función inversa es la opción positiva.
siempre se positivo. Por lo tanto, los valores permitidos de x (el dominio) deben ser x≥5. Con eso como dominio, los valores resultantes de y (el rango) son todos los valores y≥2 (si toma la solución positiva de la raíz cuadrada), o y≤2 (si elige la solución negativa de la raíz cuadrada). Recuerda que originalmente definiste el dominio como x≥2, para encontrar la función inversa. Por lo tanto, la solución correcta para la función inversa es la opción positiva.
12. Comprueba si tu función inversa funciona. Para asegurarse de que su trabajo sea correcto y que su inversa sea la ecuación correcta, elija cualquier valor para x y colóquelo en la ecuación original para encontrar y. Luego coloca ese valor de y en el lugar de x en tu ecuación inversa, y mira si obtienes el número con el que comenzaste. Si es así, entonces su función inversa es correcta.
 procesar. Esto da el resultado y=6.
procesar. Esto da el resultado y=6. . Esto devuelve y=3, que es el número con el que comenzaste. Puedes concluir que tu función inversa es correcta.
. Esto devuelve y=3, que es el número con el que comenzaste. Puedes concluir que tu función inversa es correcta.Método 3 de 3: usar la fórmula del cuadrado

1. Usa la fórmula cuadrática para resolver x. Recuerda, al resolver ecuaciones cuadráticas, hay un método para factorizarlas (si es posible). Si la factorización no funcionó, podrías usar la fórmula del cuadrado, que daría las soluciones reales a cualquier ecuación cuadrática. También puedes usar la fórmula del cuadrado como método para encontrar funciones inversas.
- La fórmula del cuadrado es x=[-b±√(b^2-4ac)]/2a.
- Tenga en cuenta que la fórmula del cuadrado produce dos soluciones posibles, una positiva y una negativa. Hará esta elección en función de determinar el dominio y el alcance de la función.

2. Comience con una ecuación cuadrática para encontrar la inversa. Su ecuación cuadrática debe comenzar en el formato  . Tome los pasos algebraicos necesarios para obtener su ecuación en esa forma.
. Tome los pasos algebraicos necesarios para obtener su ecuación en esa forma.
 . Tome los pasos algebraicos necesarios para obtener su ecuación en esa forma.
. Tome los pasos algebraicos necesarios para obtener su ecuación en esa forma. .
.
3. Trazar la ecuación para determinar el dominio y el rango. Representa gráficamente la función, ya sea usando una calculadora gráfica o trazando varios puntos hasta que puedas dibujar la parábola. Verás que esta ecuación define una parábola con el punto más alto en (-1,-4). Entonces, para definir esto como una función que tendrá una inversa, define el dominio como todos los valores de x≤-1. El rango es entonces todos los valores y≥-4.

4. Intercambiar las variables x e y. Para encontrar el inverso, intercambia las variables x e y. Deje la ecuación sin cambios, excepto intercambiar las variables. En esta etapa, reemplaza x con f(x).
 , esto da el resultado
, esto da el resultado  .
.
5. Establecer el lado izquierdo de la ecuación igual a cero. Recuerda que para usar la fórmula cuadrática tienes que igualar la ecuación a cero, luego usa los coeficientes en la fórmula. De manera similar, este método para encontrar una función inversa comienza igualando la ecuación a cero.
 .
.
6. Redefina las variables para que se ajusten a la fórmula del cuadrado. Este paso es un poco complicado. Saber que la fórmula del cuadrado resuelve x, en la ecuación  . Entonces, para la ecuación que tienes ahora,
. Entonces, para la ecuación que tienes ahora,  , para ajustarse a esa clasificación, debe redefinir los términos de la siguiente manera:
, para ajustarse a esa clasificación, debe redefinir los términos de la siguiente manera:
 . Entonces, para la ecuación que tienes ahora,
. Entonces, para la ecuación que tienes ahora,  , para ajustarse a esa clasificación, debe redefinir los términos de la siguiente manera:
, para ajustarse a esa clasificación, debe redefinir los términos de la siguiente manera: . Entonces, x=1
. Entonces, x=1 . Entonces, b=2
. Entonces, b=2 . Entonces, c=(-3-x)
. Entonces, c=(-3-x)
7. Resuelve la fórmula del cuadrado con estos valores redefinidos. Normalmente procesarías los valores de a, b y c en la fórmula del cuadrado para resolver x. Sin embargo, recuerda que previamente intercambiaste x e y para encontrar el de la función inversa. Entonces, cuando usas la fórmula del cuadrado para resolver x, en realidad estás resolviendo y, o la f-inversa. Los pasos para resolver la fórmula del cuadrado funcionan de la siguiente manera:

8. Escribe las dos soluciones posibles. Tenga en cuenta que la fórmula del cuadrado da dos resultados posibles, usando el símbolo ±. Escriba las dos soluciones separadas para que sea más fácil determinar el dominio y el rango y dar la solución final correcta. Estas dos soluciones son:



9. Determinar el dominio y el rango de la función inversa. Tenga en cuenta que para definir la raíz cuadrada, el dominio debe ser x≥-4. Recuerda que el dominio de la función original era x≤-1 y el rango era y≥-4. Para elegir la función inversa que le corresponde, necesita la segunda solución,  elegir como la función inversa correcta.
elegir como la función inversa correcta.
 elegir como la función inversa correcta.
elegir como la función inversa correcta.
10. Comprueba si tu función inversa es correcta. Para asegurarse de que su trabajo sea correcto y que su inversa sea la ecuación correcta, elija cualquier valor para x y póngalo en la ecuación original para encontrar y. Luego coloca ese valor de y en el lugar de x en tu ecuación inversa, y mira si obtienes el número con el que comenzaste. Si es así, entonces su función inversa es correcta.
 , elige tu x=-2. Esto devuelve y=-3. Ahora sustituya el valor de x=-3 en la función inversa,
, elige tu x=-2. Esto devuelve y=-3. Ahora sustituya el valor de x=-3 en la función inversa,  . Esto devuelve -2, que de hecho es el valor con el que comenzaste. Entonces tu definición de la función inversa es correcta.
. Esto devuelve -2, que de hecho es el valor con el que comenzaste. Entonces tu definición de la función inversa es correcta.Artículos sobre el tema. "Encontrar el inverso de una ecuación cuadrática"
Оцените, пожалуйста статью
Similar
Popular