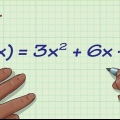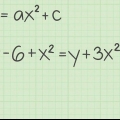Determinar los valores máximo y mínimo de una función cuadrada

Contenido

Pasos
Consejos

La coordenada y de la cresta o valle de una parábola (generalmente representada por k) es también el valor máximo o mínimo de la ecuación cuadrática representada por la parábola. Veamos cómo determinarlo!

Pasos

Método 1 de 4: Para una ecuación cuadrática de la forma y = ax + bx + c

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 1

1. Decide si quieres determinar el valor máximo o el valor mínimo. Es uno o el otro, no puedes hacer ambos.

El valor máximo o mínimo de una ecuación cuadrática es el mismo que el pico o valle de esa función.
La función y = ax + bx + c,
(c-b/4a) devuelve el valor y (el valor de la función) como el vértice.

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 1Bullet1

Si el valor de a es positivo, entonces obtienes el valor mínimo, porque la parábola en la parte superior está abierta (el vértice es el punto más bajo del gráfico).

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 1Bullet2

Si el valor de a es negativo, encontrarás el valor máximo, porque la parábola en la parte inferior está abierta (el vértice es el punto más alto del gráfico).

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 1Bullet3

El valor de a no puede ser cero, de lo contrario no estamos tratando con una ecuación cuadrática, ¿verdad??

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 1Bullet4

Método 2 de 4: Para una ecuación cuadrática en la forma y = a(x-h) + k

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 2

1. Para y = a(x-h) + k, k es el valor de la función en el vértice.

k nos da el valor máximo o mínimo de la ecuación cuadrática cuando a es negativo o positivo respectivamente.

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 2Bullet1

Método 3 de 4: Diferenciar en una ecuación cuadrática de la forma y = ax^2 + bx + c

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 3

1. Diferenciar y para x. dy/dx = 2ax + b

Imagen titulada Encuentra el valor máximo o mínimo de una función cuadrática fácilmente Paso 4

2. Determinar cuáles son los valores derivados en términos de dy/dx. Dado que dy/dx es la función derivada de una curva, la derivada de una curva se puede determinar en cualquier momento dado. Por lo tanto, el valor máximo/mínimo se puede determinar igualando estos valores a 0 y luego determinando los valores correspondientes. dy/dx = 0, 2ax+b = 0, x = -b/2a