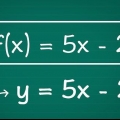Un polinomio sin raíces ni fracciones con variables en el denominador. El dominio de este tipo de función consiste en el conjunto de todos los números reales. Una función con una fracción con una variable en el denominador. Para encontrar el dominio de este tipo de función, iguala a cero el denominador de la fracción e ignora el valor de x que encuentras después de resolver la ecuación. Una función con una variable dentro de un radical. Para encontrar el dominio de este tipo de función, establezca los términos dentro del radical mayor que 0 y resuelva la ecuación para averiguar qué valores para x son correctos dentro de esta función. Una función con un logaritmo natural (ln). Haz los términos entre paréntesis >0 y resuelve. Un gráfico. Deducir de la gráfica qué valores son correctos para x. Una relación. Esta es una lista de coordenadas xey. Su dominio es simplemente una lista de coordenadas x. 
La estructura de un dominio es un corchete cuadrado/redondo abierto, seguido de los 2 extremos del dominio separados por una coma y seguidos por un corchete cuadrado/redondo de cierre. Por ejemplo: [-1.5). Esto significa que el dominio va de -1 a 5. Use corchetes como [ y ] para indicar si un número cae dentro de un cierto dominio. Entonces, en el ejemplo, [-1.5), -1 cae dentro del dominio. Usa paréntesis como ( y ) para indicar que un número está fuera de cierto dominio. Entonces, en el ejemplo, [-1.5), el 5 está fuera del dominio. El dominio se detiene en cualquier punto antes del 5, por ejemplo 4999… Utilice “U” (que significa "Unión") para conectar partes del dominio que están separadas entre sí.` Por ejemplo: [-1.5) U (5.10]. Esto significa que el dominio va de -1 a 10, pero hay una brecha en el dominio en 5. Por ejemplo, esto podría deberse a una función con "x - 5" en el denominador. puedes hacer mucho "UDS"-use símbolos según sea necesario, si el dominio tiene múltiples rupturas. Use el símbolo de infinito (en direcciones positivas y negativas) para indicar que en esa dirección el dominio es infinito. En el infinito, use siempre ( ) y no [ ]. 

f(x) = 2x/(x - 4) x - 4 = 0 (x - 2 )(x + 2) = 0 x ≠ (2, - 2) 
x = todos los números reales excepto 2 y -2 

x-7 0 
x7 
D = [7,∞) 
Ahora verifique el área debajo de -2 (por ej. -3), si esto da un resultado mayor que cero. Así es. (-3) - 4 = 5 Ahora revisa el área entre -2 y 2. Por ejemplo, toma 0. 0 - 4 = -4, entonces sabes que los números entre -2 y 2 no funcionan. Ahora pruebe con un número superior a 2, como +3. 3 - 4 = 5, por lo que los números arriba de 2 funcionan. Anota el dominio cuando hayas terminado. He aquí cómo escribir esto: re = (-∞, -2) U (2, ∞) 

x - 8 > 0 
x - 8 + 8 > 0 + 8 X > 8 
D = (8,∞) 

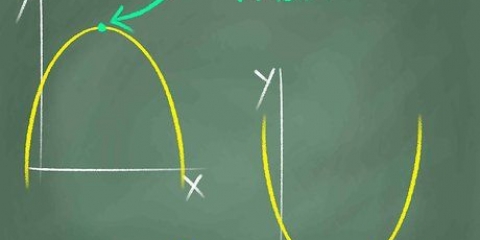
una linea. Si ve una línea en el gráfico que va al infinito, eventualmente cada valor de x estará contenido en la parábola, por lo que el dominio es igual a todos los números reales. Una parábola ordinaria. Si ve una parábola que apunta hacia arriba o hacia abajo, entonces el dominio consta de todos los números reales, porque todos los números en el eje x están finalmente contenidos en la parábola. Una parábola horizontal. Si estás tratando con una parábola con el vértice en (4,0) que se extiende infinitamente hacia la derecha, entonces tu dominio es igual a D = [4,∞) 




Hallar el dominio de una función
Contenido
- Pasos
- Método 1 de 6: aprender los conceptos básicos
- Método 2 de 6: encontrar el dominio de una función que contiene una fracción
- Método 3 de 6: Encontrar el dominio de una función con una raíz cuadrada
- Método 4 de 6: Encontrar el dominio de una función usando el logaritmo natural
- Método 5 de 6: Encontrar el dominio de una función usando un gráfico
- Método 6 de 6: determinar el dominio de una función usando una colección/relación
El dominio de una función es una colección de números que caben dentro de esa función. En otras palabras, es una colección de valores de x asociados con una ecuación dada. El conjunto de valores de y se llama rango de función. Si quieres saber cómo encontrar el dominio de una función en diferentes situaciones, sigue estos pasos.
Pasos
Método 1 de 6: aprender los conceptos básicos

1. Aprende la definición de un dominio. Un dominio de una función se define como el conjunto de todos los números reales que pueden servir como entradas para esa función. En otras palabras, un dominio es el conjunto completo de valores de x ingresados en una función, lo que da como resultado un conjunto de valores de y.

2. Aprende a encontrar el dominio de diferentes funciones. El tipo de característica determinará el mejor método para encontrar un dominio. Estos son los elementos básicos que necesitará para las siguientes funciones:

3. Entender la notación de un dominio. La notación correcta de un dominio es fácil de aprender, pero es importante que lo hagas correctamente para no perder puntos en pruebas y exámenes. Aquí hay algunas cosas que necesita saber para escribir correctamente el dominio de una función:
Método 2 de 6: encontrar el dominio de una función que contiene una fracción

1. escribir la tarea. Supongamos que tiene el siguiente problema:
- f(x) = 2x/(x - 4)

2. Para fracciones con una variable en el denominador, establece esta variable igual a cero en una ecuación. Si quieres encontrar el dominio de una función con una fracción, excluye todos los valores de x que hacen que el denominador sea igual a cero, porque nunca puedes dividir por cero. Así que escribe el denominador como una ecuación y hazlo igual a 0. Aquí está cómo hacerlo:

3. Toma nota del dominio. Aquí está cómo hacerlo:
Método 3 de 6: Encontrar el dominio de una función con una raíz cuadrada

1. escribir la tarea. Suponga que tiene el siguiente problema: Y = (x-7)

2. Asegúrese de que los términos dentro de la raíz cuadrada puedan ser mayores o iguales a 0. No puedes sacar la raíz cuadrada de un número negativo, pero puedes sacar la raíz cuadrada de cero. Tenga en cuenta que esto se aplica no solo a las raíces cuadradas, sino a todos los números de raíz pares. No se aplica a los números radicales impares, porque no es un problema si hay un número negativo debajo del signo radical. Aquí hay un ejemplo:

3. Aislar la variable. Ahora para separar x en el lado izquierdo de la ecuación, suma 7 a ambos lados del signo igual, para que después de esta operación quede así:

4. Anota el dominio correctamente. Esta es la notación correcta:

5. Encuentra el dominio de una función con una raíz cuadrada si son posibles múltiples soluciones. Suponga que tiene la siguiente función: y = 1/√( ̅x -4). Si sacas el denominador fuera de los paréntesis y lo igualas a cero obtienes x ≠ (2, - 2). He aquí cómo proceder:
Método 4 de 6: Encontrar el dominio de una función usando el logaritmo natural

1. escribir la tarea. Supongamos que tienes esto:
- f(x) = ln(x-8)

2. Hacer que los términos dentro de los paréntesis sean mayores que cero. El logaritmo natural debe ser positivo, así que haz que los términos dentro de los paréntesis sean mayores que cero. Aquí hay un ejemplo:

3. Resolver. Separe la variable x sumando 8 a ambos lados de la ecuación. Así es cómo:

4. Toma nota del dominio. Demuestre que el dominio de esta ecuación es igual a todos los números mayores que 8 hasta el infinito. Así es cómo:
Método 5 de 6: Encontrar el dominio de una función usando un gráfico

1. Ver el gráfico.

2. Investiga qué valores de x pertenecen a la gráfica. Esto es más fácil decirlo que hacerlo, así que aquí hay algunos consejos:

3. determinar el dominio. Determine el dominio en función del tipo de gráfico que tenga. Si no está muy seguro pero conoce la ecuación de la línea, ingrese las coordenadas x en la función para verificar.
Método 6 de 6: determinar el dominio de una función usando una colección/relación

1. Escribe la relación. Una relación es simplemente una serie de coordenadas x e y. Suponga que tiene las siguientes coordenadas: {(1, 3), (2, 4), (5, 7)}

2. Escribe las coordenadas x. Estos son: 1, 2, 5.

3. determinar el dominio. re = {1, 2, 5}

4. Asegúrate de que esta relación sea una función. Una relación es una función si cada vez que ingresas una coordenada x numérica obtienes la misma coordenada y como respuesta. Entonces, si pones un 3 delante de la x, obtienes 6 como el valor de y, y así sucesivamente. La siguiente relación es no una función porque obtienes dos valores de y diferentes para cada valor de "X": {(1, 4), (3, 5), (1, 5)}.
Artículos sobre el tema. "Hallar el dominio de una función"
Оцените, пожалуйста статью
Similar
Popular