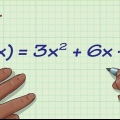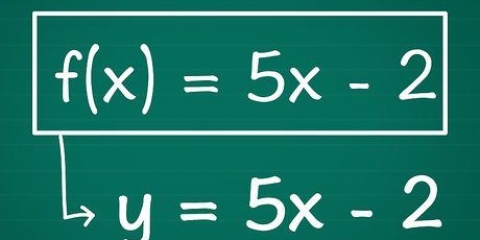Por ejemplo: la función estándar f(x) = 2x +16x + 39. Aquí tenemos a = 2, b = 16 y c = 39. En notación de vértice: f(x) = 4(x - 5) + 12. Aquí tenemos a = 4, h = 5 y k = 12. 
Ejemplo 1. (f(x) = 2x +16x + 39), h = -b/2a = -16/2(2). Resolviendo esto vemos que h = -4. Ejemplo 2. (f(x) = 4(x - 5) + 12), inmediatamente vemos que h = 5. 
Hemos visto por ejemplo 1 que h = -4. Ahora para encontrar k resolvemos esta ecuación insertando este valor de h en la ecuación, para la variable x: k = 2(-4) + 16(-4) + 39. k = 2(16) - 64 + 39. k = 32 - 64 + 39 = 7 Del ejemplo 2 sabemos que el valor de k es igual a 12, sin necesidad de un cálculo. 
En el ejemplo 1, la parte superior del gráfico es (-4.7). Dibuja el punto en tu gráfico y asegúrate de nombrar las coordenadas correctamente. En el ejemplo 2, la parte superior es (5,12). Así que desde el punto (0,0) vas 5 lugares a la derecha y luego 12 hacia arriba. 
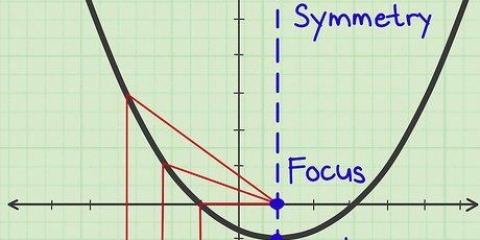
En el caso del ejemplo 1, el eje de simetría es la recta paralela al eje y que pasa por el punto (-4, 7). Aunque no es parte de la parábola en sí, resaltar ligeramente esta guía puede mostrarle qué tan simétrica es la curva de la parábola. 
En el ejemplo 1 estamos tratando con la función (f(x) = 2x +16x + 39), y esta es por tanto una parábola de valle, porque a = 2 (positivo). En el ejemplo 2 estamos tratando con la función f(x) = 4(x - 5) + 12), y esta también es una parábola de valle porque a = 4 (positivo). 
Determina que f(x) = 0 y resuelve la ecuación. Este método puede funcionar para ecuaciones cuadráticas simples, especialmente en la forma de vértice, pero encontrará que se vuelve cada vez más difícil a medida que las funciones se vuelven más complejas. Abajo hay algunos ejemplos. f(x) = 4(x - 12) 0 = 4(x - 12) - 4 4 = 4(x - 12) 1 = (x - 12) SqRt(1) = (x - 12) +/-1 = x-12. x = 11 y 13 son las intersecciones con el eje x de la parábola. Factoriza la ecuación. Algunas ecuaciones de la forma ax + bx + c se pueden reescribir fácilmente como (dx + e)(fx +g), donde dx × fx = ax, (dx × g + fx × e) = bx y e × g = C. En este caso, las intersecciones x son los valores de x donde cada término dentro de los paréntesis se convierte en 0. Por ejemplo: x + 2x + 1 = (x + 1)(x + 1) En este caso, el punto de intersección es igual a -1 porque, cuando se llena con ambos factores, da cero. Usa la fórmula abc. Si no es fácil averiguar las intersecciones o factorizar la ecuación, use el "fórmula abc" que está especialmente diseñado para esto. Suponga una ecuación en la forma ax + bx + c. Luego ingrese los valores de a, b y c en la fórmula x = (-b +/- SqRt(b - 4ac))/2a. Tenga en cuenta que esto a menudo le da dos respuestas para x, lo cual está bien, eso solo significa que su parábola tiene dos intersecciones con el eje x. Aquí hay un ejemplo: -Inserta 5x + 1x + 10 en la ecuación de la siguiente manera: x = (-1 +/- Cuadrado derecho(1 - 4(-5)(10)))/2(-5) x = (-1 +/- Cuadrado derecho(1 + 200))/-10 x = (-1 +/- Cuadrado derecho(201))/-10 x = (-1 +/- 14,18)/-10 x = (13,18/-10) y (-15,18/-10). Las intersecciones de la parábola con el eje x son aproximadamente x = -1,318 y 1,518 Como en el ejemplo 1 con la ecuación 2x + 16x + 39, esto se verá así: x = (-16 +/- Cuadrado derecho(16 - 4(2)(39))))/2(2) x = (-16 +/- Cuadrado derecho(256 - 312))/4 x = (-16 +/- Cuadrado derecho(-56)/-10 Como no es posible encontrar la raíz cuadrada de un número negativo, sabemos que no existen intersecciones con el eje x para esta parábola en particular. 
Por ejemplo, sabemos que nuestra ecuación cuadrática 2x + 16x + 39 tiene un punto de intersección y = 39, pero también podemos encontrar esto de la siguiente manera: f(x) = 2x + 16x + 39 f(x) = 2(0) + 16(0) + 39 f(x) = 39. La intersección de la parábola con el eje y: y = 39. Como se indicó anteriormente, podemos leer fácilmente la intersección porque y = c. La ecuación 4(x - 5) + 12 tiene una intersección con el eje y que se puede encontrar de la siguiente manera: f(x) = 4(x - 5) + 12 f(x) = 4(0 - 5) + 12 f(x) = 4(-5) + 12 f(x) = 4(25) + 12 f(x) = 112. La intersección con el eje y: y = 112. 
Echemos otro vistazo a la ecuación x + 2x + 1. Ya sabemos que la única intersección con el eje x es (-1.0). Como solo es tangente al eje x en este punto, podemos inferir que el vértice de la gráfica es igual a este punto. Hasta ahora solo tenemos un punto de esta parábola, no lo suficiente como para poder dibujar un gráfico. Busquemos algunos puntos más para asegurarnos de que tenemos más valores. Intentemos encontrar los valores de y asociados con los siguientes valores de x: 0, 1, -2 y -3. x=0: f(x) = (0) + 2(0) + 1 = 1. Entonces el punto es (0.1). x=1: f(x) = (1) + 2(1) + 1 = 4. Entonces el punto es (1,4). x=-2: f(x) = (-2) + 2(-2) + 1 = 1. Entonces el punto es (-2.1). x=-3: f(x) = (-3) + 2(-3) + 1 = 4. Entonces el punto es (-3.4). Coloca estos puntos en el gráfico y dibuja tu parábola. Tenga en cuenta que la parábola es completamente simétrica: si conoce los puntos de un lado del gráfico, por lo general puede ahorrarse mucho trabajo usando estos puntos para encontrar los puntos del otro lado del eje de simetría.
Graficar una función
Como un gráfico ve una ecuación cuadrática hacha + bx + c, también cualquier escrito comoa(x - h) + k, parece una curva suave en forma de U. Esto es lo que llamamos un parábola. Graficar una ecuación cuadrática implica encontrar el vértice, la dirección y, a menudo, las intersecciones con el eje x y el eje y. En el caso de la ecuación cuadrática relativamente simple, también puede ser suficiente ingresar una cantidad de valores para x para indicar estos puntos en el sistema de coordenadas, después de lo cual se puede dibujar la parábola. Continúe con el paso 1 para comenzar.
Pasos

1. Determina qué tipo de ecuación cuadrática tienes. Esto se puede escribir de dos maneras: la notación estándar y la notación de vértice (otra forma de escribir la fórmula de la raíz cuadrada). Puedes usar ambos para hacer un gráfico de una ecuación cuadrática, pero este proceso es ligeramente diferente en ambos casos. Por lo general, encontrará la forma estándar, pero ciertamente no está de más aprender a usar ambas formas. Las dos formas de una ecuación cuadrática son: La forma del vértice. Aquí la ecuación cuadrática se escribe como: f(x) = a(x - h) + k donde a, h y k son números reales y a no es igual a cero. Esta forma se llama vértice porque h y k se refieren directamente al vértice de tu parábola en el punto (h,k). Dos ejemplos de ecuaciones en forma de vértice son f(x) = 9(x - 4) + 18 y -3(x - 5) + 1 Para poder hacer un gráfico de estas ecuaciones, primero determinamos la parte superior (h,k) del gráfico. En la ecuación estándar puedes encontrar esto a través de: h = -b/2a y k = f(h), mientras que ya se da en forma de vértice porque h y k aparecen en la ecuación.
- La forma estándar. Aquí la ecuación cuadrática se escribe como: f(x) = ax + bx + c donde a, b y c son números reales y a no es igual a cero.
- Dos ejemplos de ecuaciones cuadráticas estándar: f(x) = x + 2x + 1 y f(x) = 9x + 10x -8.

2. Determina tus variables. Para resolver una ecuación cuadrática, generalmente es necesario determinar las variables a, b y c (o a, h y k). Un problema ordinario le dará una ecuación cuadrática en la forma estándar, pero la notación de vértice también puede ocurrir.

3. calcular h. En la notación de vértice, el valor de h ya está dado, pero en la notación estándar, este valor aún no se ha calculado. Recuerda que para la ecuación estándar, h = -b/2a.

4. calcular k. Al igual que con h, k ya se conoce para ecuaciones en forma de vértice. Para ecuaciones en notación estándar, recuerda que k = f(h). En otras palabras, puedes encontrar k reemplazando cada variable x con el valor de h.

5. Dibuja la parte superior o inferior del gráfico. La cresta o valle de su parábola es el punto (h, k) - h representa la coordenada x y k representa la coordenada y. La cresta es el centro de tu parábola: el punto más alto o más bajo, la cresta o el valle, de un gráfico en forma de "UDS" o viceversa. Ser capaz de determinar el vértice de una parábola es una parte esencial para poder dibujar un gráfico correcto; a menudo, determinar el vértice de una parábola es parte de un problema de matemáticas en la escuela.

6. Dibuja el eje de simetría de la parábola. El eje de simetría de una parábola es la línea que corta la figura en el medio y la divide exactamente por la mitad. Un lado del gráfico se refleja a lo largo de esta línea en el otro lado del gráfico. Para ecuaciones cuadráticas de la forma ax + bx + c o a(x - h) + k, este eje es la línea paralela al eje y que pasa por el vértice de la parábola.

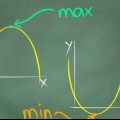
7. Determinar la dirección de la parábola. Después de averiguar cuál es la parte superior de la parábola, es necesario saber si se trata de una parábola de montaña o una parábola de valle, es decir, si la abertura está en la parte inferior o en la parte superior. Afortunadamente esto es muy simple. Si "a" seguro que se trata de una parábola de valle; es "a" negativo entonces es una parábola de montaña (con la abertura en la parte inferior)

8. Determine, si es necesario, las intersecciones de la parábola. A menudo, en los problemas de matemáticas, se le pide que proporcione las intersecciones de la parábola con el eje x (estos son "cero", a o dos puntos donde la parábola interseca o toca el eje x). Incluso si no se solicitan, estos puntos son muy importantes para poder dibujar un gráfico preciso. Pero no todas las parábolas se cruzan con el eje x. Si está tratando con una parábola de valle y el punto del valle está sobre el eje x o, en el caso de una parábola de montaña, justo debajo del eje x, entonces simplemente no hay intersecciones que encontrar. Si es así, utilice uno de los siguientes métodos:

9. Si es necesario, determine la intersección de la parábola con el eje y. A menudo no es necesario, pero a veces se requiere para encontrar este punto de intersección, por ejemplo, para un problema de matemáticas. Esto es bastante fácil: establezca el valor de x en 0 y resuelva la ecuación para f (x) o y, lo que le da el valor y del punto donde la parábola se cruza con el eje y. La diferencia con las intersecciones a través del eje x es que con el eje y siempre hay un solo punto de intersección. Nota: para las ecuaciones estándar, la intersección con el eje y está en y = c.

10. Si lo encuentra necesario, primero dibuje puntos adicionales y luego el gráfico completo. Ahora debería tener un pico o valle, una dirección, intersecciones con el eje x y posiblemente con el eje y de su ecuación. Desde este punto, puede intentar dibujar la parábola usando estos puntos o puede intentar encontrar más puntos para que el gráfico sea más preciso. La forma más fácil de hacer esto es simplemente completando una cantidad de valores x, lo que devuelve una cantidad de valores y. A menudo se le pedirá (por el maestro) que primero calcule una cantidad de puntos antes de poder dibujar la parábola.
Consejos
- Redondea números si es necesario o usa fracciones. Esto puede ayudar a mostrar un gráfico correctamente.
- Nótese que si, para la función f(x) = ax + bx + c, b o c son iguales a cero, esos términos desaparecerán. Por ejemplo, 12x + 0x + 6 es igual a 12x + 6 porque 0x es igual a 0.
Artículos sobre el tema. "Graficar una función"
Оцените, пожалуйста статью
Popular