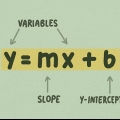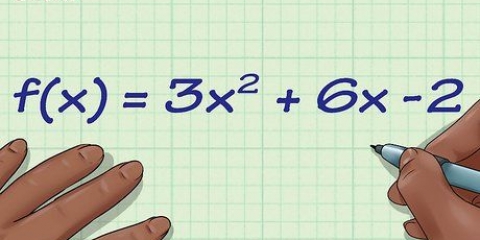Instrucciones de paso a paso gratis 
Si el coeficiente (pendiente) a en la ecuación es positiva, la parábola abre hacia arriba (en una parábola orientada verticalmente), si la letra mayúscula es `U` y el vértice es un mínimo. como el a negativo, la parábola se abre hacia abajo y el vértice tiene un máximo. Si tiene problemas para recordar esto, piénselo de esta manera: una ecuación con un positivo un parece una sonrisa; una comparación con un negativo un parece un ceño fruncido. Digamos que tienes la siguiente ecuación: y = 2x -1. Esta parábola tiene forma de `U` porque la a (2) es positivo. Si la ecuación tiene un término y en lugar de un término x en la segunda potencia, entonces la parábola estará orientada horizontalmente y abierta hacia los lados (hacia la derecha o hacia la izquierda), como una `C` o una `C` invertida. Por ejemplo: la parábola y = x + 3 abre a la derecha, como una `C`. 
En el ejemplo anterior (y = 2x² -1), . es a = 2 y b = 0`.` Ahora puedes calcular el eje de simetría completando los números:x = -0 / (2)(2) = 0`.` En este caso, el eje de simetría es x = 0 (es decir, el eje y del sistema de coordenadas). 
Las coordenadas del vértice también se llaman (h, k). En este caso h igual a 0 y k igual a -1. La ecuación de la parábola se puede escribir en la forma y = a(x - h)² + k. De esta forma, el vértice es el punto (h, k) y no es necesario hacer ningún cálculo para encontrar el vértice que no sea la interpretación correcta de la gráfica. 
El valor medio de x debe ser el eje de simetría en el caso de una parábola `vertical`. Debe incluir al menos dos valores por encima y por debajo del valor medio de x en la tabla de simetría. En este ejemplo colocas el valor del eje de simetría (x = 0) en el medio de la tabla. 
Si x = -2, entonces y: y = (2) (-2) - 1 = 8 - 1 = 7 Si x = -1, entonces y: y = (2) (-1) - 1 = 2 - 1 = 1 Si x = 0, entonces y: y = (2) (0) - 1 = 0 - 1 = -1 Si x = 1, entonces y: y = (2) (1) - 1 = 2 - 1 = 1 Si x = 2, entonces y: y = (2) (2) - 1 = 8 - 1 = 7 
El eje x es horizontal, el eje y es vertical. Los números positivos en el eje y están arriba y los números negativos debajo del punto (0, 0). Los números positivos en el eje x están a la derecha y los números negativos a la izquierda del punto (0, 0). 
Dibujar una parábola
Una parábola es una curva simétrica de espejo bidimensional que tiene la forma de un arco. Cada punto de la parábola es equidistante de un punto fijo (el foco) y una línea recta fija (la directriz). Para mapear una parábola, debe encontrar la parte superior de la parábola, así como algunos puntos a cada lado, para marcar el camino que recorren los puntos.
Pasos
Parte 1 de 2: dibujar una parábola
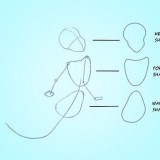
1. Comprender las partes de una parábola. Es posible que reciba cierta información antes de comenzar, y conocer la terminología lo ayudará a evitar pasos innecesarios. Estas son las partes de la parábola que necesitas saber:
- El foco. Un punto fijo en el interior de la parábola que se utiliza para la definición formal de la curva.
- el director. Una línea sólida y recta. La parábola es el lugar geométrico o conjunto de puntos en los que un punto dado equidista del enfocar y el directora se encuentra. (Ver gráfico arriba.)
- El eje de simetría. Esta es una línea recta que pasa por el vértice de la parábola y equidista de los puntos correspondientes en los dos brazos de la parábola.
- el vértice. El punto donde el eje de simetría interseca a la parábola se llama vértice de la parábola. Si la parábola se abre hacia arriba o hacia la derecha, el vértice es un mínimo de la curva. Si la parábola se abre hacia abajo o hacia la izquierda, el vértice es un máximo.
2. Saber la ecuación de una parábola. La ecuación general de una parábola es y = ax+ bx + c. También se puede escribir en la forma aún más general y = a(x – h)² + k, pero nos centraremos aquí en la primera forma de la ecuación.
3. Encuentra el eje de simetría. Recuerda que el eje de simetría es la recta que pasa por el punto de inflexión (vértice) de la parábola. En el caso de una parábola vertical (valle o montaña), el eje es igual a la coordenada x del vértice, es decir, el valor x del punto donde el eje de simetría interseca a la parábola. Usa esta fórmula para encontrar el eje de simetría: x = -b/2a.
4. Encuentra el vértice. Una vez que conozca el eje de simetría, puede sustituir ese valor por x para obtener la coordenada y. Estas dos coordenadas te dan el vértice de la parábola. En este caso, reemplaza 0 en 2x -1 para obtener la coordenada y. y = 2 x 0 -1 = 0 -1 = -1. El vértice es (0,-1) y la parábola corta el eje y en -1.
5. Crear una tabla de valores para x. Crea una tabla con ciertos valores para x en la primera columna. Esta tabla te da las coordenadas que necesitas para graficar la ecuación.
6. Calcular los valores de las coordenadas y correspondientes. Sustituye cualquier valor de x en la ecuación de la parábola y calcula los valores correspondientes de y. Ponga estos valores calculados de y en la tabla. En este ejemplo, los valores de y se calculan de la siguiente manera:
7. Ingrese los valores calculados de y en la tabla. Ahora ha encontrado al menos cinco pares de coordenadas para la parábola y está casi listo para dibujar la parábola. Según su trabajo, ahora tiene los siguientes puntos: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Recuerda que la parábola (simétrica) se representa con respecto al eje de simetría. Esto significa que las coordenadas y de los puntos directamente opuestos entre sí con respecto al eje de simetría serán iguales. Las coordenadas y asociadas con las coordenadas x -2 y +2 son ambas 7; las coordenadas y pertenecientes a las coordenadas x -1 y +1 son ambas 1, y así sucesivamente.
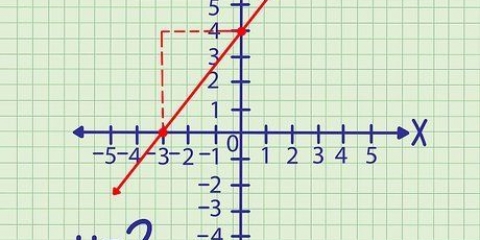
8. Dibujar los puntos de la tabla en el sistema de coordenadas. Cada fila de la tabla forma un par de coordenadas (x, y) en el sistema de coordenadas. Dibuja todos los puntos usando las coordenadas en la tabla.
9. Conecta los puntos. Para graficar la parábola, conecte los puntos dibujados en el paso anterior. El gráfico en este ejemplo parece una U. Conecte los puntos usando líneas ligeramente curvas (en lugar de rectas). Esto crea la imagen más precisa de la parábola (que está ligeramente curvada en toda su longitud). En cualquier extremo de la parábola, puede dibujar flechas que apunten lejos del vértice, si lo desea. Esto indica que la parábola continúa indefinidamente.
Parte 2 de 2: desplazar la gráfica de una parábola
Si desea una forma más rápida de desplazar una parábola sin tener que volver a encontrar su vértice y volver a especificar diferentes puntos en la parábola, entonces necesita comprender la ecuación de una parábola y aprender a convertirla vertical u horizontalmente. Comience con la parábola básica: y = x. Tiene un vértice en el punto (0, 0) y es una parábola de valle. Algunos puntos de la gráfica son: (-1, 1), (1, 1), (-2, 4) y (2, 4). Puedes desplazar una parábola según la ecuación.
1. Mover una parábola hacia arriba. Considere la ecuación y = x +1. Esto desplaza la parábola original una unidad hacia arriba. El vértice ahora es (0, 1) en lugar de (0, 0). Su forma no ha cambiado, pero cada coordenada y se desplazará una unidad hacia arriba. Entonces, en lugar de (-1, 1) y (1, 1), dibujamos los puntos (-1, 2) y (1, 2).
2. Mover una parábola hacia abajo. Toma la ecuación y = x-1. Desplazamos la parábola original una unidad hacia abajo para que el vértice ahora sea (0, -1) en lugar de (0, 0,). Seguirá teniendo la misma forma que la parábola original, pero cada coordenada y se desplazará una unidad hacia abajo. Entonces, en lugar de (-1, 1) y (1, 1), por ejemplo, dibujamos (-1, 0) y (1, 0).
3. Mover una parábola a la izquierda. Considere la ecuación y = (x + 1). Esto desplaza la parábola original una unidad hacia la izquierda. El vértice ahora es (-1, 0) en lugar de (0, 0). La forma de la parábola original sigue siendo la misma, pero cada coordenada x se desplaza uno hacia la izquierda. Por ejemplo, en lugar de (-1, 1) y (1, 1), dibujamos (-2, 1) y (0, 1).
4. Mover una parábola a la derecha. Considere la ecuación y = (x - 1). Esta es la parábola original desplazada una unidad a la derecha. El vértice ahora es (1, 0) en lugar de (0, 0). La forma de la parábola original sigue siendo la misma, pero cada coordenada x se desplaza un lugar a la derecha. Por ejemplo, en lugar de (-1, 1) y (1, 1), dibujamos (0, 1) y (2, 1).
Artículos sobre el tema. "Dibujar una parábola"
Оцените, пожалуйста статью
Popular
