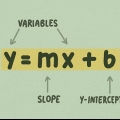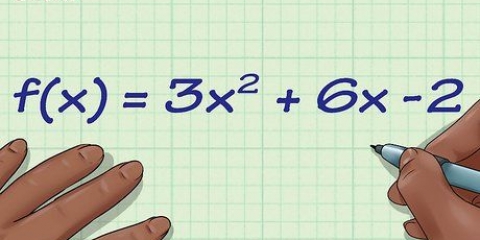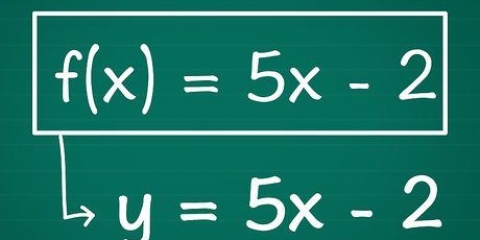Si la pendiente es negativa, significa que la recta baja cuando vas hacia la derecha. 





-1: -1 + 2 = 1 0: 0 +2 = 2 1: 1 + 2 = 3 




Hacer F(x) igual a cero:
Resolver:




Algunas funciones cuadráticas, como  nunca son negativos. Entonces hay una asíntota en 0.
nunca son negativos. Entonces hay una asíntota en 0. A menos que esté trabajando con números imaginarios, esto no es posible: 
Las ecuaciones con exponentes complejos pueden tener muchas asíntotas. 
para la comparacion  , podrías completar -1, 0, 1, -2, 2, -10 y 10. Esto le da un buen rango de números para comparar.
, podrías completar -1, 0, 1, -2, 2, -10 y 10. Esto le da un buen rango de números para comparar. Sea inteligente al seleccionar números. En el ejemplo, notará rápidamente que un signo negativo no importa; por ejemplo, puede dejar de probar -10, porque será lo mismo que 10. 
Suponga de dos a cuatro valores grandes para x, mitad negativos y mitad positivos, y dibuje los puntos. ¿Qué sucede si inserta `infinito` para una variable?? ¿La función se vuelve infinitamente más grande o más pequeña?? Si los grados son iguales en una fracción, como  , luego solo divide los dos primeros coeficientes (
, luego solo divide los dos primeros coeficientes ( para obtener su asíntota final (-0.5).
para obtener su asíntota final (-0.5). Si los grados en una fracción son diferentes, divida la ecuación en el numerador por la ecuación en el denominador usando la división polinomial larga. 

Dibujar la gráfica de una función
Contenido
Un gráfico de una función es una representación visual del comportamiento de una función en un plano x-y. Los gráficos nos ayudan a comprender varios aspectos de la función que serían difíciles de comprender con solo observar la función en sí. Puede graficar miles de ecuaciones y hay diferentes fórmulas para cada ecuación. Sin embargo, siempre hay formas de graficar una función si olvidaste los pasos exactos para el tipo específico de función.
Pasos
Método 1 de 3: grafica una ecuación lineal con una tangente

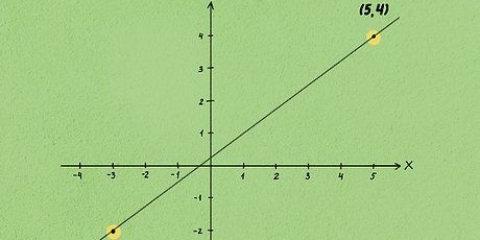
1. Sepa que las funciones lineales son líneas simples que son fáciles de dibujar, como y = 2 X + 5  . Hay una variable y una constante, escritas como
. Hay una variable y una constante, escritas como  en una función lineal, sin exponentes, radicales, etc. Si tienes una ecuación tan simple, la gráfica de la función también es simple. Otros ejemplos de funciones lineales son:
en una función lineal, sin exponentes, radicales, etc. Si tienes una ecuación tan simple, la gráfica de la función también es simple. Otros ejemplos de funciones lineales son:
 . Hay una variable y una constante, escritas como
. Hay una variable y una constante, escritas como  en una función lineal, sin exponentes, radicales, etc. Si tienes una ecuación tan simple, la gráfica de la función también es simple. Otros ejemplos de funciones lineales son:
en una función lineal, sin exponentes, radicales, etc. Si tienes una ecuación tan simple, la gráfica de la función también es simple. Otros ejemplos de funciones lineales son: 
2. Use la constante para indicar la intersección con el eje y. La intersección con el eje y es el punto donde la función cruza el eje y en su gráfico. En otras palabras, es el punto donde  . Entonces, para encontrarlo, simplemente establezca x en cero y deje la constante en la ecuación. En el ejemplo anterior,
. Entonces, para encontrarlo, simplemente establezca x en cero y deje la constante en la ecuación. En el ejemplo anterior,  , es la intersección con el eje y igual a y=5, es decir, el punto (0.5). Marque este lugar en su gráfico con un punto.
, es la intersección con el eje y igual a y=5, es decir, el punto (0.5). Marque este lugar en su gráfico con un punto.
 . Entonces, para encontrarlo, simplemente establezca x en cero y deje la constante en la ecuación. En el ejemplo anterior,
. Entonces, para encontrarlo, simplemente establezca x en cero y deje la constante en la ecuación. En el ejemplo anterior,  , es la intersección con el eje y igual a y=5, es decir, el punto (0.5). Marque este lugar en su gráfico con un punto.
, es la intersección con el eje y igual a y=5, es decir, el punto (0.5). Marque este lugar en su gráfico con un punto.
3. Encuentra la pendiente de tu línea con el número justo antes de la variable. en el ejemplo,  , es la pendiente `2`. Eso es porque 2 pertenece a la variable `x`. La pendiente indica qué tan inclinada es una línea o qué tan alta va la línea antes de girar a la derecha o a la izquierda. Una pendiente más grande significa una línea más empinada.
, es la pendiente `2`. Eso es porque 2 pertenece a la variable `x`. La pendiente indica qué tan inclinada es una línea o qué tan alta va la línea antes de girar a la derecha o a la izquierda. Una pendiente más grande significa una línea más empinada.
 , es la pendiente `2`. Eso es porque 2 pertenece a la variable `x`. La pendiente indica qué tan inclinada es una línea o qué tan alta va la línea antes de girar a la derecha o a la izquierda. Una pendiente más grande significa una línea más empinada.
, es la pendiente `2`. Eso es porque 2 pertenece a la variable `x`. La pendiente indica qué tan inclinada es una línea o qué tan alta va la línea antes de girar a la derecha o a la izquierda. Una pendiente más grande significa una línea más empinada.
4. Hacer una fracción de la pendiente. La pendiente tiene que ver con la inclinación, y la inclinación es simplemente la diferencia entre el movimiento hacia arriba y hacia abajo, y hacia la izquierda y hacia la derecha. La pendiente es una fracción de el cambio de y comparado con el cambio de x. ¿Cuánto debe la línea `cambiar sobre y` antes de `cambiar sobre x`?? En el ejemplo, la pendiente `2` se puede leer como  .
.
 .
.
5. Comience en su intersección con el eje y y siga los cambios sobre y y x, para dibujar más puntos. Una vez que sepas la pendiente, úsala para dibujar tu función lineal. Comience en la intersección con el eje y, aquí (0.5), luego suba 2 y a la derecha 1. Marca también este punto (1,7). Encuentre otros 1-2 puntos para dibujar el gráfico.

6. Usa una regla para conectar tus puntos y graficar tu función lineal. Para evitar errores o gráficos toscos, encuentre y conecte al menos tres puntos separados, aunque dos serán suficientes en caso de emergencia. Esta es la gráfica de tu ecuación lineal!
Método 2 de 3: estimar puntos en un gráfico

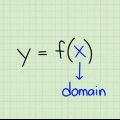
1. Determinar la función. Toma la función de la forma F(X), cierto y representa el rango, X representa el dominio, y F la función. Como ejemplo usamos y = x+2, por lo cual F(X) = x+2.

2. Dibuja dos líneas cruzadas en una hoja de papel. La linea horizontal eres tu X-ceniza. La linea vertical eres tu y-ceniza.

3. Numere su gráfico. Resalta tanto el X-como si el y-eje con números equidistantes entre sí. Para el X-eje son los números positivos a la derecha y negativos a la izquierda. Para el y-eje son los números positivos en la parte superior y negativos en la parte inferior.

4. Calcular un y-valor para 2-3 X-valores. Asumir la función F(X) = x+2. Calcula algunos valores para y por los valores correspondientes para X visible en el eje de la función. Para ecuaciones más complicadas, puede ser necesario simplificar la función, aislando primero una variable.

5. Dibuja el punto del gráfico para cada par. Dibuja líneas verticales delgadas imaginarias a lo largo de la X-eje y horizontalmente a lo largo del y-ceniza. El punto donde se cruzan estas líneas es un punto gráfico (o simplemente use papel cuadriculado).

6. Elimina las lineas imaginarias. Cuando haya dibujado todos los puntos del gráfico, puede borrar las líneas imaginarias. Nota: la gráfica de f(x) = x sería una línea paralela a ella a través del origen (0,0), pero f(x) = x+2 se desplaza dos unidades (a lo largo del eje y) en la cuadrícula por el +2 en la ecuación.
Método 3 de 3: Graficar una función compleja

1. Comprender cómo representar gráficamente tipos comunes de ecuaciones. Hay tantas estrategias de gráficos diferentes como tipos de funciones, demasiadas para cubrirlas completamente aquí. Si encuentra esto difícil y una estimación no funciona, consulte los artículos sobre:
- Funciones cuadráticas
- Funciones racionales
- Funciones logarítmicas
- Desigualdades (sin características, pero con información útil).

2.Primero determine los ceros. Los ceros son los puntos donde el gráfico se cruza con la línea horizontal en el gráfico. Si bien no todos los gráficos tienen ceros, la mayoría sí, y es el primer paso que debe tomar para que todo salga bien. Para encontrar ceros, primero establece toda la función en cero y luego resuélvela. Por ejemplo:







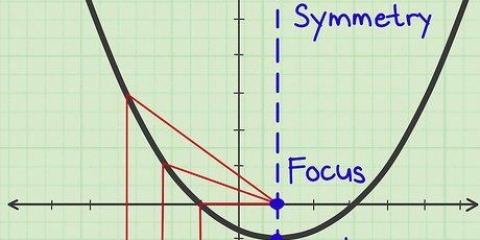
3. Encuentre y marque cualquier asíntota horizontal (lugares donde la función es imposible de alcanzar) con una línea de puntos. Por lo general, estos son puntos donde el gráfico no existe, como cuando se divide por cero. Si tu ecuación tiene una variable en una fracción, como  , luego comience poniendo a cero la parte inferior de la fracción. Puede mapear todos los lugares donde es igual a cero (en este ejemplo, una línea de puntos en x=2 y x=-2), porque nunca puede dividir por cero. Sin embargo, las fracciones no son los únicos lugares para encontrar asíntotas. Por lo general, todo lo que necesita es algo de sentido común:
, luego comience poniendo a cero la parte inferior de la fracción. Puede mapear todos los lugares donde es igual a cero (en este ejemplo, una línea de puntos en x=2 y x=-2), porque nunca puede dividir por cero. Sin embargo, las fracciones no son los únicos lugares para encontrar asíntotas. Por lo general, todo lo que necesita es algo de sentido común:
 , luego comience poniendo a cero la parte inferior de la fracción. Puede mapear todos los lugares donde es igual a cero (en este ejemplo, una línea de puntos en x=2 y x=-2), porque nunca puede dividir por cero. Sin embargo, las fracciones no son los únicos lugares para encontrar asíntotas. Por lo general, todo lo que necesita es algo de sentido común:
, luego comience poniendo a cero la parte inferior de la fracción. Puede mapear todos los lugares donde es igual a cero (en este ejemplo, una línea de puntos en x=2 y x=-2), porque nunca puede dividir por cero. Sin embargo, las fracciones no son los únicos lugares para encontrar asíntotas. Por lo general, todo lo que necesita es algo de sentido común: nunca son negativos. Entonces hay una asíntota en 0.
nunca son negativos. Entonces hay una asíntota en 0.

4. Aplicar los valores y dibujar diferentes puntos. Simplemente elija algunos valores para x y resuelva la función. Luego haz un gráfico de los puntos en tu gráfico. Cuanto más complicado sea el gráfico, más puntos necesitarás. En general, -1, 0 y 1 son los puntos más fáciles de obtener, aunque querrá tener dos o tres más a cada lado del cero para obtener un buen gráfico.
 , podrías completar -1, 0, 1, -2, 2, -10 y 10. Esto le da un buen rango de números para comparar.
, podrías completar -1, 0, 1, -2, 2, -10 y 10. Esto le da un buen rango de números para comparar.
5. Mapee el comportamiento final de la función para ver qué sucede cuando se vuelve realmente grande. Esto le da una idea de la dirección general de una función, por lo general como un vertical asíntota. Por ejemplo: sabes que  eventualmente se vuelve muy, muy grande. Solo una `x` adicional (un millón versus un millón y uno) hace que y sea mucho más grande. Hay algunas formas de probar el comportamiento final, que incluyen:
eventualmente se vuelve muy, muy grande. Solo una `x` adicional (un millón versus un millón y uno) hace que y sea mucho más grande. Hay algunas formas de probar el comportamiento final, que incluyen:
 eventualmente se vuelve muy, muy grande. Solo una `x` adicional (un millón versus un millón y uno) hace que y sea mucho más grande. Hay algunas formas de probar el comportamiento final, que incluyen:
eventualmente se vuelve muy, muy grande. Solo una `x` adicional (un millón versus un millón y uno) hace que y sea mucho más grande. Hay algunas formas de probar el comportamiento final, que incluyen: , luego solo divide los dos primeros coeficientes (
, luego solo divide los dos primeros coeficientes ( para obtener su asíntota final (-0.5).
para obtener su asíntota final (-0.5).
6. Conecte los puntos, evitando el comportamiento asintótico y final, para estimar el gráfico. Una vez que tenga cinco o seis puntos, las asíntotas y una idea general del comportamiento final, use todo esto para construir una versión aproximada del gráfico.

7. Dar gráficos perfectos usando una calculadora gráfica. Las calculadoras gráficas son poderosas computadoras de mano que pueden proporcionar gráficos exactos para cualquier ecuación. Le permiten ubicar puntos exactos, encontrar líneas de pendiente y visualizar ecuaciones difíciles con facilidad. Simplemente ingrese la ecuación exacta en la sección del gráfico (generalmente un botón con la etiqueta `F (x) =`) y presione el botón del gráfico para tener una idea de la función.
Consejos
- Las calculadoras gráficas son una excelente manera de practicar. Intente hacer un gráfico a mano y luego use la calculadora para obtener una imagen perfecta del gráfico, luego compare ambos gráficos.
- Si realmente ya no sabes qué hacer, solo ingresa algunos puntos. Básicamente, podrías dibujar toda la función de esta manera, si probaras una cantidad infinita de combinaciones de números.
Artículos sobre el tema. "Dibujar la gráfica de una función"
Оцените, пожалуйста статью
Similar
Popular