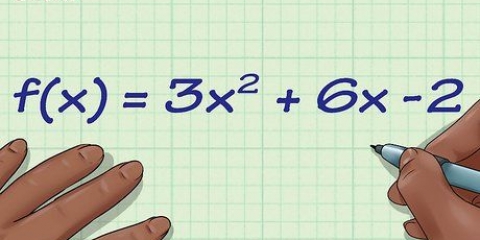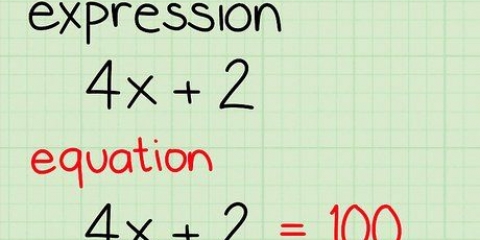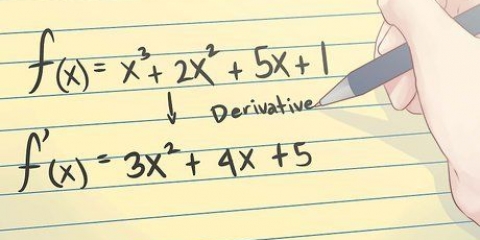Encontrar el inverso de una función: 5 pasos (con fotos)

Contenido

Pasos
Consejos

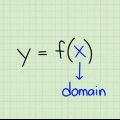
Una función en matemáticas (generalmente anotada como f(x)) puede considerarse como una especie de fórmula o programa en el que ingresa un valor "X" se mete, que luego devuelve un valor dado para y. El inverso de una función f(x) (anotada como f(x)) es esencialmente lo contrario: ingrese un y-valor y obtienes el anterior X-valor de vuelta. Encontrar el inverso de una función puede parecer complicado, pero para ecuaciones simples, todo lo que necesita es cierto conocimiento de las operaciones básicas de álgebra. Lee las siguientes instrucciones paso a paso y fíjate bien en el ejemplo.

Pasos

Imagen titulada Hallar algebraicamente el inverso de una función Paso 01

1. Escribe tu función, intercambiando f(x) con y si necesario. Tu fórmula pertenece y tener de un lado el signo igual y del otro lado el X-condiciones. Si ya tienes una ecuación escrita en y y X términos (como por ejemplo 2 + y = 3x), entonces solo necesita y se resuelve aislándolo.

Ejemplo: Tenemos una función f(x) = 5x - 2, y la reescribimos como y = 5x - 2, simplemente por "f(x)" para ser reemplazado por y.
Nota: f(x) es la notación de función estándar, pero si se trata de varias funciones, a cada función se le asignará una letra inicial diferente para que sea más fácil distinguirlas. Por ejemplo, g(x) y h(x) son letras comúnmente utilizadas para funciones.

Imagen titulada Algebraicamente encuentra el inverso de una función Paso 02

2. suelto X sobre. En otras palabras, haga las ediciones necesarias para X aislar a un lado del signo igual. Para hacer esto, usa las operaciones básicas del álgebra: si X tiene un coeficiente (un número para la variable), divida ambos lados de la ecuación por este número para cancelarlo; ¿Hay una constante dentro de la "X"-término, luego resuelva sumando o restando ambos lados del signo igual, y así sucesivamente.

Recuerde que toda operación en un lado del signo igual debe hacerse también en el otro lado.

Ejemplo: Para continuar con nuestro ejemplo, primero sumamos 2 en ambos lados de la ecuación. Esto nos da y + 2 = 5x. Luego dividimos ambos lados de la ecuación por 5, quedando (y + 2)/5 = x. Finalmente, para hacerlo más legible, reescribimos la ecuación con la "X" A la izquierda: x = (y + 2)/5.

Imagen titulada Algebraicamente encuentra el inverso de una función Paso 03

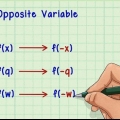
3. Intercambiar las variables. Intercambio X de y y viceversa. La ecuación resultante es la inversa de la función original. En otras palabras, si tenemos un valor para X completar nuestra ecuación original, entonces podemos completar la respuesta en sentido inverso (nuevamente para "X") que devuelve el valor original!

Ejemplo: después de intercambiar x e y, obtenemos y = (x + 2)/5

Imagen titulada Algebraicamente encuentra el inverso de una función Paso 04

4. reemplazar y por medio de "f(x)". Las funciones inversas generalmente se expresan como f(x) = (x términos) . Recuerda que en este caso el exponente -1 no significa que tengamos que realizar una operación exponencial sobre la función. Es solo una forma de indicar que esta función es la inversa de la original.

Porque X es igual a 1/x, también puedes escribir f(x) como "1/f(x)," otra notación para el inverso de f(x).

Imagen titulada Hallar algebraicamente el inverso de una función Paso 05

5. Revisa tu trabajo. Intente completar una constante en la función original para X. Si encontraste el inverso correcto, entonces encontrarías el valor original de "X" debería verlo de nuevo, si ingresa el resultado de esto en sentido inverso.

Ejemplo: Ingresemos 4 como el valor de X en nuestra comparación original. Esto nos da f(x) = 5(4) - 2, o f(x) = 18.

A continuación, vamos a introducir este resultado en el inverso. Así que sustituimos 18 en la función inversa como el valor de X. Al hacer esto obtenemos como resultado y = (18 + 2)/5 y esto es igual a y = 4. Así que 4 es el valor de x con el que empezamos y con eso sabemos que hemos encontrado la función inversa correcta.

Consejos

Puedes usar ambas notaciones f(x) = y y f^(-1)(x) = y sin ningún problema si haces operaciones matemáticas en las funciones. Pero es mejor mantener separadas la función original y la función inversa, así que trate de mantenerla en notación común. En el caso de la función inversa la notación f^(-1)(x).
Tenga en cuenta que la inversa de una función suele ser, pero no siempre, una función en sí misma.