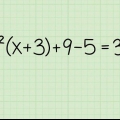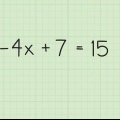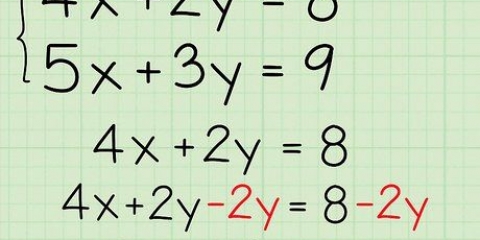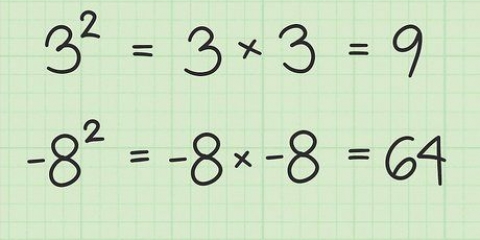3x + 5 + 4x - x + 2x + 9 = 3x - x + 4x + 2x + 5 + 9 = 2x + 6x + 14 
3x + 15 = 9x + 30 Ves que todo coeficiente es divisible por 3. Elimina el número 3 dividiendo cada término por 3 para simplificar la ecuación. 3x/3 + 15/3 = 9x/3 + 30/3 = x + 5 = 3x + 10 
(3 + 5) × 10 + 4 Primero las operaciones entre paréntesis: = (8) × 10 + 4 Entonces vamos a elevar el poder: = 64 x 10 + 4 Luego la multiplicación: = 640 + 4 Y finalmente sumamos: = 644 
5x + 15 = 65 = 5x/5 + 15/5 = 65/5 = X + 3 = 13 = X = 10 

2x + 12 = 44 Primero resta 12 de ambos lados. 2x + 12 -12 = 44 -12 = 2x = 32 Ahora divide ambos lados por 2. 2x/2 = 32/2 = X = 16 Resuelve sacando la raíz cuadrada de ambos lados, porque eso hace que x sea igual a x. √x = √16 = Da ambas respuestas: x = 4, -4 
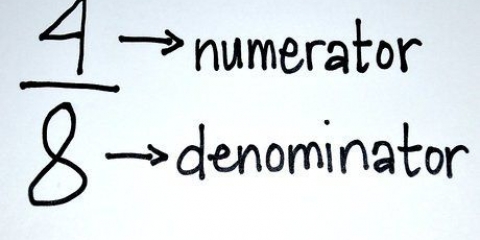
(x + 3)/6 = 2/3 Primero vas a multiplicar en cruz para deshacerte de la fracción. Multiplicar el numerador de una fracción por el denominador de la otra fracción. (x + 3) x 3 = 2 x 6 = 3x + 9 = 12 Luego combinas términos iguales. Combine los términos constantes 9 y 12, restando 9 de ambos lados. 3x + 9 - 9 = 12 - 9 = 3x = 3 Aísla la variable, x, dividiendo ambos lados por 3 y tienes la respuesta. 3x/3 = 3/3 = X = 1 
√(2x+9) - 5 = 0 Primero, mueve todo lo que no esté bajo el radical al otro lado de la ecuación: √(2x+9) = 5 Luego eleva al cuadrado ambos lados para eliminar el radical: (√(2x+9)) = 5 = 2x + 9 = 25 Ahora puedes resolver la ecuación como de costumbre, combinando las constantes y aislando la variable: 2x = 25 - 9 = 2x = 16 x = 8 
Así es como calculas esto para el valor absoluto aislando el valor absoluto y luego eliminándolo: |4x +2| - 6 = 8 = |4x +2| = 8 + 6 = |4x +2| = 14 = 4x + 2 = 14 = 4x = 12 x = 3 Ahora resuelve esto nuevamente invirtiendo el signo del término en el otro lado de la ecuación, después de haber aislado el valor absoluto: |4x +2| = 14 = 4x + 2 = -14 4x = -14 -2 4x = -16 4x/4 = -16/4 = X = -4 Ahora da ambas respuestas: x = -4, 3
Resolver una expresión algebraica
Contenido
Una expresión algebraica es una expresión matemática que contiene números y/o variables. Aunque no se puede resolver porque no contiene el signo igual (=), se puede simplificar. Sin embargo, puedes resolver ecuaciones matematicas, que contienen expresiones algebraicas separadas por un signo igual. Si desea dominar este concepto matemático, siga leyendo hasta el paso 1 para comenzar.
Pasos
Parte 1 de 2: comprensión de los conceptos básicos

1. Comprender la diferencia entre una expresión algebraica y una ecuación algebraica. Una expresión algebraica es una expresión matemática que contiene números y/o variables. No contiene un signo igual y no se puede resolver. Sin embargo, una ecuación algebraica se puede resolver e involucra una serie de expresiones algebraicas separadas por un signo igual. Aquí hay unos ejemplos:
- Expresión algebraica: 4x + 2
- Ecuación algebraica: 4x + 2 = 100

2. Aprende a combinar términos semejantes. Combinar términos semejantes simplemente significa sumar (o restar) los términos del mismo grado. Esto significa que todos los términos x se pueden combinar con otros términos x, todos los términos x se pueden combinar con términos x y todas las constantes (números que no están vinculados a variables, como 8 o 5) también se pueden sumar o combinar con El uno al otro. Aquí hay un ejemplo:

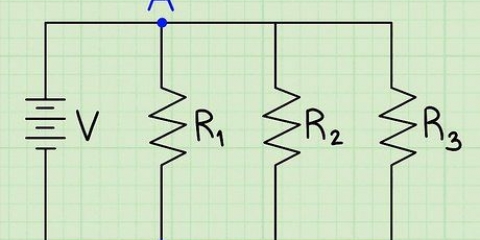
3. Aprende a factorizar un número. Si estás tratando con una ecuación algebraica, lo que significa que hay una expresión a cada lado de un signo igual, puedes simplificar esto eliminando el término común. Mire los coeficientes de todas las condiciones (los números antes de las variables o las constantes) y vea si hay un número que pueda "resolver" dividiendo cada término por ese número. Si puede hacer esto, entonces ha simplificado la ecuación y está en camino de resolverla. Así es como funciona esto:

4. Conocer el orden de las operaciones. El orden de las operaciones, también conocido como el mnemotécnico `Cómo deshacerse de los insuficientes`, indica el orden en el que debes realizar las diferentes operaciones matemáticas. El orden es: Paréntesis, Exponenciación, Enraizamiento, Multiplicación, División, Suma y Resta. He aquí un ejemplo de cómo funciona el orden de las operaciones:

5. Aprende a aislar una variable. Si desea resolver una ecuación algebraica, su objetivo es colocar la variable, a menudo conocida como x, en un lado de la ecuación y los términos constantes en el otro lado de la ecuación. Puede aislar x dividiendo, multiplicando, sumando, restando, determinando la raíz cuadrada u otras operaciones. Una vez que haya aislado x, puede comenzar a resolverlo. Así es como se hace esto:
Parte 2 de 2: Resolver una ecuación algebraica

1. Resolver una ecuación algebraica lineal simple. Una ecuación algebraica lineal es agradable y simple, usando solo las constantes y variables de primer grado (sin potencias u otra complejidad). Para resolver esto, todo lo que necesita hacer es multiplicar, dividir, sumar o restar cuando sea necesario, para aislar la variable y resolver para `x`. Así es como se hace esto:
- 4x + 16 = 25 -3x =
- 4x = 25 -16 - 3x
- 4x + 3x = 25 -16 =
- 7x = 9
- 7x/7 = 9/7 =
- x = 9/7

2. Resolver una ecuación algebraica con potencias (exponentes). Si la ecuación tiene potencias, entonces todo lo que necesitas hacer es encontrar una manera de aislar la potencia en un lado de la ecuación y luego resolverla "eliminando" la potencia al encontrar la raíz cuadrada tanto de la potencia como de la constante en el otro lado de la ecuación. Así es como se hace esto:

3. Resolver una expresión algebraica con fracciones. Para resolver una expresión algebraica que contiene fracciones, debe cruzar las fracciones, combinar términos similares y luego aislar la variable. Así es como se hace esto:

4. Resolver una expresión algebraica. Si está tratando con una expresión algebraica con radicales, todo lo que necesita hacer es encontrar una manera de elevar al cuadrado ambos lados para que pueda eliminar el radical para resolver la variable. Así es como se hace esto:

5. Resolver una expresión algebraica que contiene un valor absoluto. El valor absoluto de un número representa su valor sin importar si es positivo o negativo; el valor absoluto siempre es positivo. Entonces, por ejemplo, el valor absoluto de -3 (también conocido como |3|) es solo 3. Para encontrar el valor absoluto, aísle el valor absoluto y luego resuelva para x dos veces (tanto para x donde el valor absoluto simplemente se elimina, como para x donde los términos en el otro lado del signo igual han cambiado de signo, de positivo a negativo y viceversa). Esto va así:
Consejos
- Para verificar dos veces su respuesta, puede ir a wolfram-alpha.com ir. Allí puede obtener la respuesta, que a menudo se muestra en los dos pasos.
- Una vez que haya terminado, reemplace la variable con la respuesta, luego resuelva la suma para ver si es correcta. Si es así, enhorabuena, has terminado! Acabas de resolver una ecuación algebraica!
- El grado de un polinomio es la potencia más alta dentro de los términos.
Artículos sobre el tema. "Resolver una expresión algebraica"
Оцените, пожалуйста статью
Popular