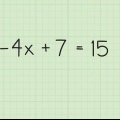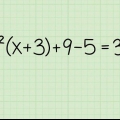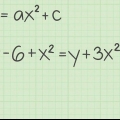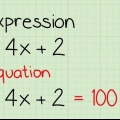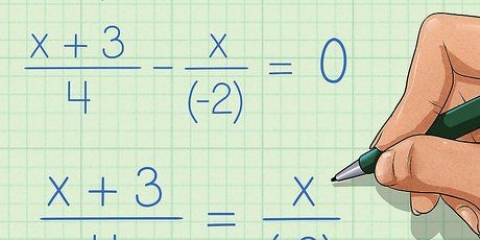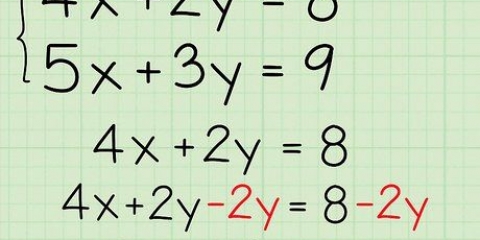Usar la propiedad distributiva para resolver una ecuación

Contenido

Pasos
Consejos

La propiedad distributiva es una regla matemática para simplificar una ecuación con paréntesis. Probablemente aprendiste desde el principio que primero tienes que hacer las operaciones entre paréntesis, pero con expresiones algebraicas, eso no siempre es posible. La propiedad distributiva te permite multiplicar el término fuera del paréntesis por los términos dentro. Tienes que tener cuidado de hacerlo de la manera correcta, de lo contrario puedes perder información y la comparación ya no es correcta. También puedes usar la propiedad distributiva para simplificar ecuaciones con fracciones.

Pasos

Método 1 de 4: usar la propiedad distributiva fundamental

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 1

1. Multiplique el término fuera de paréntesis por cualquier término dentro de paréntesis. Para hacer esto, esencialmente divides el término externo entre los términos internos. Multiplique el término fuera de paréntesis por el primer término dentro de paréntesis. Luego lo multiplicas por el segundo término. Si hay más de dos términos, continúe distribuyendo el término fuera de los paréntesis entre todos los términos dentro de los paréntesis. Simplemente deje los operadores (más o menos) dentro de los paréntesis.

$2 (X - 3) = 10$ $2(x-3)=10$
$2 (X) - (2) (3) = 10$ $2(x)-(2)(3)=10$
$2 X - 6 = 10$ $2x-6=10$

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 2

2. Combinar términos semejantes. Antes de que puedas resolver la ecuación, debes combinar términos semejantes. Combinar todos los términos numéricos entre sí. Además, combina todos los términos variables por separado. Para simplificar la ecuación, ordena los términos de modo que las variables estén a un lado del signo igual y las constantes (solo los números) estén al otro lado.

2 X - 6 = 10

$2x-6=10$ ....(problema inicial)

2 X - 6 (+ 6) = 10 (+ 6)

$2x-6(+6)=10(+6)$ .... (suma 6 en ambos lados)

2 X = dieciséis

$2x=16$ .... (Variable izquierda; constante derecha)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 3

3. Resuelve la ecuación. suelto

X

$X$ dividiendo ambos lados de la ecuación por el coeficiente de la variable.

2 X = dieciséis

$2x=16$ ....(problema inicial)

2 X / 2 = dieciséis / 2

$2x/2=16/2$ ....(dividir ambos lados por 2)

X = 8

$x=8$ ....(solución)

Método 2 de 4: distribuir coeficientes negativos

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 4

1. Distribuir un número negativo junto con el signo menos. Si va a multiplicar un término o términos entre paréntesis por un número negativo, asegúrese de aplicar el signo menos a cada término entre paréntesis.

Recuerda las reglas básicas para multiplicar por números negativos:

Menos x Menos = Más.
menos x más = menos.

Mira el siguiente ejemplo:

- 4 (9 - 3 X) = 48

$-4(9-3x)=48$ .... (problema inicial)

- 4 (9) - (- 4) (3 X) = 48

$-4(9)-(-4)(3x)=48$ ....(multiplique -4 por cada término)

- 36 - (- 12 X) = 48

$-36-(-12x)=48$ ....(simplificar la multiplicación)

- 36 + 12 X = 48

$-36+12x=48$ ....(tenga en cuenta que `menos -12` es lo mismo que +12)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 5

2. Combinar términos semejantes. Una vez que haya completado la distribución, debe simplificar la ecuación, moviendo todos los términos variables a un lado del signo igual y todos los números sin variables al otro lado. Haces esto por medio de una combinación de suma o resta.

- 36 + 12 X = 48

$-36+12x=48$ ....(problema inicial)

- 36 (+ 36) + 12 X = 48 + 36

$-36(+36)+12x=48+36$ ....(suma 36 a cada lado)

12 X = 84

$12x=84$ ....(simplifique la suma para aislar la variable)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 6

3. Comparte para obtener la solución final. Resuelva la ecuación dividiendo ambos lados de la ecuación por el coeficiente de la variable. Esto debería dar como resultado una sola variable en un lado de la ecuación, con el resultado en el otro lado.

12 X = 84

$12x=84$ ....(problema inicial)

12 X / 12 = 84 / 12

$12x/12=84/12$ ....(divide ambos lados por 12)

X = 7

$x=7$ ....(solución)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 7

4. Tratar la resta como suma (desde -1). Cuando ves un signo menos en un problema de álgebra, especialmente si está antes de un paréntesis, esencialmente dice + (-1). Esto ayuda a distribuir correctamente el signo menos en todos los términos entre paréntesis. Luego resuelve el problema como antes.

Por ejemplo, considere el problema,

4 X - (X + 2) = 4

$4x-(x+2)=4$ . Para asegurarse de que distribuyó correctamente el signo menos, reescriba el problema de esta manera:

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$

Luego distribuye -1 sobre los términos entre paréntesis, de la siguiente manera:

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$ ....(problema modificado)

4 X - X - 2 = 4

$4x-x-2=4$ ....(multiplique -1 por x y por 2)

3 X - 2 = 4

$3x-2=4$ ....(combinar términos)

3 X - 2 + 2 = 4 + 2

$3x-2+2=4+2$ ....(añadir 2 en ambos lados)

3 X = 6

$3x=6$ ....(simplificar términos)

3 X / 3 = 6 / 3

$3x/3=6/3$ ....(dividir ambos lados por 3)

X = 2

$x=2$ ....(solución)

Método 3 de 4: usa la propiedad distributiva para simplificar fracciones

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 8

1. Averiguar si hay coeficientes fraccionarios o constantes. A veces es posible que necesite resolver un problema con fracciones como coeficientes o constantes. Puedes dejarlos como están y aplicarles las reglas fundamentales del álgebra, para resolver el problema. Sin embargo, al usar la propiedad distributiva, a menudo puede simplificar la solución al convertir las fracciones en números enteros.

Mira el siguiente ejemplo $X - 3 = \frac{X}{3} + \frac{1}{6}$ $x-3={frac{x}{3}}+{frac{1}{6}}$ . Las fracciones en este ejemplo son $\frac{X}{3}$ ${frac{x}{3}}$ y $\frac{1}{6}$ ${frac{1}{6}}$ .

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 9

2. Encuentra el Mínimo Común Múltiplo (MCM) para todos los denominadores. En este paso puedes ignorar todos los enteros. Solo mira las fracciones y determina el LCF para todos los denominadores. Determinar el kgf buscando el número más pequeño que sea múltiplo de los denominadores de ambas fracciones en la ecuación. En este ejemplo, los denominadores son 3 y 6, entonces 6 es el kgf.

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 10

3. Multiplica todos los términos de la ecuación por el kgf. Recuerda, puedes aplicar cualquier operación a una ecuación matemática, siempre y cuando lo hagas en ambos lados. Multiplicando cada término de la ecuación por el lcg, los términos se anulan entre sí y se "convierten" en números enteros. Coloca tus paréntesis alrededor de todo el lado izquierdo y derecho de la ecuación, luego haz la distribución:

X - 3 = \frac{X}{3} + \frac{1}{6}

$x-3={frac{x}{3}}+{frac{1}{6}}$ ....(ecuación original)

(X - 3) = (\frac{X}{3} + \frac{1}{6})

$(x-3)=({frac{x}{3}}+{frac{1}{6}})$ ....(aplicar paréntesis)

6 (X - 3) = 6 (\frac{X}{3} + \frac{1}{6})

$6(x-3)=6({frac{x}{3}}+{frac{1}{6}})$ ....(multiplique ambos lados por el kgf)

6 X - 6 (3) = 6 (\frac{X}{3}) + 6 (\frac{1}{6})

$6x-6(3)=6({frac{x}{3}})+6({frac{1}{6}})$ ....(distribuir la multiplicación)

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(simplificar la multiplicación)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 11

4. Combinar términos semejantes. Combine todos los términos para que todas las variables estén en un lado de la ecuación y todas las constantes estén en el otro lado. Usar las operaciones básicas de suma y resta para mover términos de un lado de la ecuación al otro.

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(problema simplificado)

6 X - 2 X - 18 = 2 X - 2 X + 1

$6x-2x-18=2x-2x+1$ ....(restar 2x de ambos lados)

4 X - 18 = 1

$4x-18=1$ ....(simplificar menos suma)

4 X - 18 + 18 = 1 + 18

$4x-18+18=1+18$ ....(suma 18 en ambos lados)

4 X = 19

$4x=19$ ....(simplificar suma)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 12

5. Resuelve la ecuación. Encuentre la solución final dividiendo ambos lados de la ecuación por el coeficiente de la variable. Esto te deja con x en un lado de la ecuación y la solución numérica en el otro.

4 X = 19

$4x=19$ ....(problema personalizado)

4 X / 4 = 19 / 4

$4x/4=19/4$ ....(divide ambos lados entre 4)

X = \frac{19}{4} o 4 \frac{3}{4}

$x={frac{19}{4}}{texto{ o }}4{frac{3}{4}}$ ....(solución final)

Método 4 de 4: distribuir una fracción con una ecuación

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 13

1. Interpretar una fracción con una ecuación como una división distribuida. A veces ves un problema con varios términos en el numerador de una fracción, por encima de un denominador común. Tienes que tratar esto como un problema distributivo y aplicar el denominador a cada término del numerador. Puedes reescribir la fracción para mostrar la distribución. Como sigue:

$4 X + 8 2 = 4$ ${frac{4x+8}{2}}=4$ .....(problema inicial)
$4 X 2 + \frac{8}{2} = 4$ ${frac{4x}{2}}+{frac{8}{2}}=4$ .....(multiplicar el denominador por cada término del numerador)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 14

2. Simplifica cada numerador como una fracción separada. Después de distribuir el divisor entre cada término, puede simplificar cada término individualmente.

4 X 2 + \frac{8}{2} = 4

${frac{4x}{2}}+{frac{8}{2}}=4$ .....(problema personalizado)

2 X + 4 = 4

$2x+4=4$ .....(simplificar las fracciones)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 15

3. Aislar la variable. Continúe resolviendo el problema aislando la variable en un lado de la ecuación y moviendo los términos constantes al otro lado. Haz esto a través de una combinación de sumas y restas, cuando sea necesario.

2 X + 4 = 4

$2x+4=4$ .....(problema personalizado)

2 X + 4 - 4 = 4 - 4

$2x+4-4=4-4$ .....(restar 4 de ambos lados)

2 X = 0

$2x=0$ .....(aislar x en un lado)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 16

4. Dividir por el coeficiente para resolver el problema. En el último paso se divide por el coeficiente de la variable. Esto da la solución final, con la única variable en un lado de la ecuación y la solución numérica en el otro.

2 X = 0

$2x=0$ .....(problema personalizado)

2 X / 2 = 0 / 2

$2x/2=0/2$ .....(dividir ambos lados por 2)

X = 0

$x=0$ .....(solución)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 17

5. Evite el error común de compartir solo un término. Es tentador (pero incorrecto) dividir el primer término del numerador por el denominador y eliminar la fracción. Un error como este se vería así para el problema anterior:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema inicial)

2 X + 8 = 4

$2x+8=4$ .....(solo 4x se divide por 2, en lugar del contador completo)

2 X + 8 - 8 = 4 - 8

$2x+8-8=4-8$

2 X = - 4

$2x=-4$

X = - 2

$x=-2$ ..... (solución incorrecta)

Imagen titulada Usa la propiedad distributiva para resolver una ecuación Paso 18

6. Comprueba la corrección de tu solución. Siempre puede verificar su trabajo insertando su solución en el problema original. Cuando quieres simplificar, tienes que llegar a una afirmación verdadera. Si simplifica y obtiene una declaración incorrecta como respuesta, entonces su solución es incorrecta. En este ejemplo, prueba las dos soluciones para x = 0 y x = -2 para ver cuál es la correcta.

Comience con la solución x=0:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema inicial)

4 (0) + 8 2 = 4

${frac{4(0)+8}{2}}=4$ .....(sustituya 0 por x)

0 + 8 2 = 4

${frac{0+8}{2}}=4$

\frac{8}{2} = 4

${frac{8}{2}}=4$

4 = 4

$4=4$ .....(Cierto. Esta es la solución correcta.)

Pruebe la `solución incorrecta para x=-2:

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problema inicial)

4 (- 2) + 8 2 = 4

${frac{4(-2)+8}{2}}=4$ .....(ingrese -2 para x)

- 8 + 8 2 = 4

${frac{-8+8}{2}}=4$

\frac{0}{2} = 4

${frac{0}{2}}=4$

0 = 4

$0=4$ .....(Declaración incorrecta. Por lo tanto x=-2 es falso.)

Consejos

También puedes usar la propiedad distributiva para simplificar algunas multiplicaciones. Puede dividir números en decenas con un resto para facilitar el cálculo mental. Por ejemplo, puedes reescribir 8 x 16 como 8(10+6). Esto es simplemente 80 + 48 = 128. Otro ejemplo, 7 x 24 = 7(20 + 4) = 7(20) + 7(4) = 140 + 28 = 168. Practícalos de memoria y la aritmética mental será mucho más fácil.