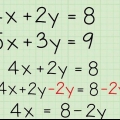2x - 2x = 0 4 años - 2 años = 2 años 8 - 2 = 6 2x + 4y = 8-(2x + 2y = 2)=0 +2y = 6 
2 años = 6 Divide 2y y 6 entre 2 y obtienes y = 3 
Inserta y = 3 en la ecuación 2x + 2y = 2 y resuelve para x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Has resuelto el sistema de ecuaciones por resta. (x, y) = (-2, 3) 
Completa (-2, 3) para (x, y) en la ecuación 2x + 4y = 8. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Completa (-2, 3) para (x, y) en la ecuación 2x + 2y = 2. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6y + -6y = 0 8 + 4 = 12 Si combinas esto obtienes un nuevo producto: 3x + 6y = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Divide 4x y 12 entre 3 para obtener x = 3 
Reemplaza x = 3 en la ecuación x - 6y = 4 para encontrar y. 3 - 6 años = 4 -6 años = 1 Divide -6y y 1 entre -6 para obtener y = -1/6. Has resuelto el sistema de ecuaciones con suma. (x, y) = (3, -1/6) 
Completa (3, -1/6) para (x, y) en la ecuación 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Completa (3, -1/6) para (x, y) en la ecuación x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - y = 2) 4x - 2y = 4 
3x + 2y = 10 + 4x - 2y = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - y = 2 -y = -2 y = 2 Has resuelto el sistema de ecuaciones usando la multiplicación. (x, y) = (2, 2) 
Completa (2, 2) para (x, y) en la ecuación 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Completa (2, 2) para (x, y) en la ecuación 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4y --> 2x + 3y = 9 2(2 - 4 años) + 3 años = 9 4 - 8 años + 3 años = 9 4 - 5y = 9 -5 años = 9 - 4 -5 años = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4y x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Resolviste el sistema de ecuaciones usando sustitución. (x, y) = (6, -1) 
Completa (6, -1) para (x, y) en la ecuación 2x + 3y = 9. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Completa (6, -1) para (x, y) en la ecuación x + 4y = 2. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Resolver un sistema de ecuaciones
Contenido
Resolver un sistema de ecuaciones requiere encontrar el valor de múltiples variables en múltiples ecuaciones. Puedes resolver un sistema de ecuaciones usando sumas, restas, multiplicaciones o sustituciones. Si quieres aprender a resolver un sistema de ecuaciones, solo tienes que seguir estos pasos.
Pasos
Método 1 de 4: resolver por resta

1. Escribe una ecuación sobre la otra. Resolver estas ecuaciones con restas es un método ideal si ves que ambas ecuaciones tienen la misma variable con el mismo coeficiente y signo. Por ejemplo, si ambas ecuaciones tienen la variable -2x, puedes usar la resta para encontrar el valor de ambas variables.
- Escribe una ecuación encima de la otra para que las variables x e y de ambas ecuaciones y los números estén uno debajo del otro. Coloque el signo menos al lado del número inferior.
- Por ejemplo: si tienes las siguientes dos ecuaciones: 2x + 4y = 8 y 2x + 2y = 2, se vería así:
- 2x + 4y = 8
- -(2x + 2y = 2)

2. Restar términos semejantes. Ahora que las dos ecuaciones están alineadas, todo lo que necesitas hacer es restar los términos similares. Haga esto con un término a la vez:

3. Resolver para el término restante. Elimina cualquier cero de la ecuación que se ha creado, no cambia el valor, y resuelve la ecuación restante.

4. Introduzca el valor encontrado de la variable en una de las ecuaciones. Ahora que sabe que y = 3, puede reemplazar este valor en la ecuación original para resolver x. No importa qué ecuación elijas, la respuesta es la misma. Así que usa la ecuación más simple!

5. Comprueba tu respuesta. Para asegurarse de que su respuesta sea correcta, ingrese ambas respuestas en ambas ecuaciones. Así es como se hace:
Método 2 de 4: resolver por suma

1. Escribe una ecuación sobre la otra. Resolver un sistema de ecuaciones por adición es el mejor método, si notas que ambas ecuaciones tienen una variable con el mismo coeficiente, pero con diferente signo; por ejemplo, si una ecuación contiene la variable 3x y la otra la variable -3x.
- Escribe una ecuación encima de la otra para que las variables x e y de ambas ecuaciones y los números estén uno debajo del otro. Coloque el signo más al lado del número inferior.
- Por ejemplo: tienes las siguientes dos ecuaciones 3x + 6y = 8 y x - 6y = 4, luego escribe la primera ecuación encima de la segunda como se muestra a continuación:
- 3x + 6y = 8
- +(x - 6y = 4)

2. Agregar términos similares juntos. Ahora que las dos ecuaciones están alineadas una encima de la otra, todo lo que necesitas hacer es sumar los términos con la misma variable:

3. Resolver para el término restante. Eliminar cualquier cero de la ecuación que haya surgido, no cambia el valor. Resuelve la ecuación restante.

4. Introduzca el valor encontrado de esta variable en una de las ecuaciones. Ahora que sabe que x = 3, puede reemplazar este valor en la ecuación original para resolver y. No importa qué ecuación elijas, la respuesta es la misma. Así que usa la ecuación más simple!

5. Comprueba tu respuesta. Para asegurarse de que su respuesta sea correcta, ingrese ambas respuestas en ambas ecuaciones. Así es como se hace:
Método 3 de 4: resolver por multiplicación

1. Escribe una ecuación sobre la otra. Escribe una ecuación encima de la otra para que las variables x e y de ambas ecuaciones y los números estén uno debajo del otro. Si está usando la multiplicación, lo está haciendo porque ninguna de las variables tiene coeficientes iguales, ahora mismo.
- 3x + 2y = 10
- 2x - y = 2

2. Asegurar coeficientes iguales. Luego, multiplique una o ambas ecuaciones por un número, de modo que una de las variables tenga el mismo coeficiente. En este caso, puede multiplicar toda la segunda ecuación por 2 para que -y sea igual a -2y y, por lo tanto, el primer coeficiente y. Así es como se hace:

3. Sumar o restar las ecuaciones. Ahora todo lo que tienes que hacer es eliminar términos iguales sumando o restando. Dado que aquí se trata de 2y y -2y, tiene sentido utilizar el método de suma porque es igual a 0. Si está tratando con 2y + 2y, use el método de resta. Aquí hay un ejemplo de cómo usar el método de suma para eliminar variables:

4. Resolver esto para el término restante. Esto se resuelve fácilmente encontrando el valor del término que aún no has eliminado. Si 7x = 14, entonces x = 2.

5. Introduzca el valor encontrado en una de las ecuaciones. Ingrese el término en una de las ecuaciones originales para resolver el otro término. Elija la ecuación más simple para esto, esta es la más rápida.

6. Comprueba tu respuesta. Para asegurarse de que su respuesta sea correcta, ingrese ambas respuestas en ambas ecuaciones. Así es como se hace:
Método 4 de 4: resolver por sustitución

1. Aislar una variable. La sustitución es ideal cuando uno de los coeficientes en una de las ecuaciones es igual a 1. Entonces todo lo que tienes que hacer es aislar esta variable a un lado de la ecuación para encontrar su valor.
- Si estás trabajando con las ecuaciones 2x + 3y = 9 y x + 4y = 2, entonces tienes que aislar x en la segunda ecuación.
- x + 4y = 2
- x = 2 - 4y

2. Completa el valor de la variable que aislaste en la otra ecuación. Toma el valor de la variable aislada y conéctalo a la otra ecuación. Por supuesto, no en la misma ecuación, de lo contrario no resolverás nada. Aquí hay un ejemplo de cómo hacer eso:

3. Resolver para la variable restante. Ahora que sabes que y = - 1, reemplaza este valor en la ecuación más simple para encontrar el valor de x. Aquí hay un ejemplo de cómo hacer eso:

4. Comprueba tu respuesta. Para asegurarse de que su respuesta sea correcta, ingrese ambas respuestas en ambas ecuaciones. Así es como se hace:
Consejos
- Ahora debería poder resolver cualquier sistema lineal de ecuaciones usando suma, resta, multiplicación o sustitución, pero un método suele ser el más adecuado dependiendo de las ecuaciones.
Artículos sobre el tema. "Resolver un sistema de ecuaciones"
Оцените, пожалуйста статью
Popular