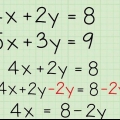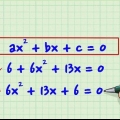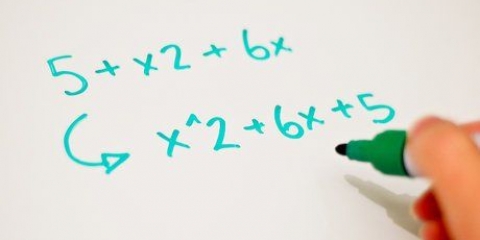Por ejemplo, la variable 12y se puede reescribir como el producto de los factores de 12 y y. Podemos escribir 12y como 3(4y), 2(6y), etc., usando los factores de 12 que sean más convenientes. Incluso podemos ir tan lejos como 12y varias veces disolver. En otras palabras, no tenemos que detenernos en 3(4y) o 2(6y) - podemos factorizar 4y y 6y en 3(2(2y) y 2(3(2y) respectivamente). Aparentemente estas dos expresiones son equivalentes entre sí. 
Intentemos un problema de ejemplo. Para factorizar la ecuación 12x + 6, primero buscamos el mcd de 12x y 6. 6 es el número más grande que divide tanto a 12x como a 6, por lo que podemos simplificar la ecuación a 6(2x + 1). Este proceso también se aplica a las ecuaciones que involucran números negativos y fracciones. x/2 + 4, por ejemplo, se puede simplificar a 1/2 (x + 8) y -7x + -21 se puede factorizar en -7 (x + 3). 

Por ejemplo, toma la ecuación cuadrática x + 5x + 6 = 0. Como 3 x 2 = 6 y 3 + 2 = 5, la ecuación simplificada se convierte en (x + 3)(x + 2). Se pueden encontrar ligeras variaciones en esta solución rápida simple en la ecuación misma: Si la ecuación cuadrática tiene la forma x-bx+c, entonces su respuesta se verá así: (x - _)(x - _). Si tiene la forma x+bx+c, entonces su respuesta se verá así: (x + _)(x + _). Si tiene la forma x-bx-c, su respuesta se verá así: (x + _)(x - _). Nota: Los espacios en blanco pueden ser fracciones o decimales. Por ejemplo, la ecuación x + (21/2)x + 5 = 0 se factoriza en (x + 10)(x + 1/2). 
Hagamos una tarea de ejemplo. 3x - 8x + 4 parece un poco intimidante al principio. Pero si nos damos cuenta de que 3 tiene solo dos factores (3 y 1), entonces se vuelve mucho más fácil, porque sabemos que nuestra respuesta debe ser de la forma (3x +/- _)(x +/- _). En este caso, ingresar -2 en los espacios en blanco dará la respuesta correcta. -2 × 3x = -6x y -2 × x = -2x. -6x + -2x = -8x. -2 × -2 = 4, entonces vemos que los términos factorizados entre paréntesis multiplicados juntos, tienen la ecuación original como producto. 
Por ejemplo, la ecuación x + 6x + 9 satisface esta forma. 3 es 9 y 3 × 2 es 6. Entonces sabemos que los factores de esta ecuación son iguales a (x + 3)(x + 3) o (x + 3). 
Volvamos a la ecuación x + 5x + 6 = 0. La ecuación resuelta es (x + 3)(x + 2) = 0. Si uno de estos factores es igual a 0, entonces toda la ecuación es 0, por lo que las posibles respuestas para x son aquellos números donde (x + 3) y (x + 2) son iguales a 0. Estos números son -3 y -2 respectivamente. 
Aplicamos -2 y -3 a x + 5x + 6 = 0. Primero: -2: (-2) + 5(-2) + 6 = 0 4 + -10 + 6 = 0 0 = 0. Esto es correcto, entonces -2 es una respuesta válida. Ahora intentamos -3: (-3) + 5(-3) + 6 = 0 9 + -15 + 6 = 0 0 = 0. Esto también es correcto, por lo que -3 también es una respuesta válida. 

La ecuación 4x + 8xy + 4y se puede reescribir como 4x + (2 × 2 × 2)xy + 4y. Ahora queda claro que está en la forma correcta, por lo que podemos afirmar con cierta confianza que nuestra ecuación se puede factorizar en (2x + 2y). 
Por ejemplo: 8x - 27y se puede factorizar en (2x - 3y)(4x + ((2x)(3y)) + 9y).
Factorización de ecuaciones
Contenido
En matemáticas es factorizar determinar números o expresiones que, cuando se multiplican entre sí, dan un valor o ecuación particular. La factorización es una habilidad útil para aprender cuando se resuelven problemas matemáticos simples; la capacidad de factorizar correctamente se vuelve casi esencial cuando se trata de ecuaciones cuadráticas y otros polinomios. La factorización se puede utilizar para simplificar ecuaciones matemáticas simples y facilitar su resolución. El factoring puede permitirte descartar posibles respuestas mucho más rápido que si tuvieras que revisar cada una de ellas.
Pasos
Método 1 de 3: factorización de números y ecuaciones simples

1. Comprender la definición de factorización en números. La factorización es simple en principio, pero en la práctica puede ser bastante desafiante cuando se resuelven ecuaciones complejas. Por lo tanto, el enfoque más simple es comenzar con números pequeños y luego con ecuaciones simples antes de pasar a aplicaciones más avanzadas. El factores de un número dado son los números que, multiplicados entre sí, dan ese único número. Por ejemplo, los factores de 12 son 1, 12, 2, 6, 3 y 4, porque 1 × 12, 2 × 6 y 3 × 4 tienen 12 como su producto.
- Otra forma de pensar en esto es que los factores de un número dado son aquellos números que forman el número en se puede compartir en su totalidad.
- ¿Puedes encontrar todos los factores de 60?? Usamos el número 60 para varias aplicaciones (la cantidad de minutos en una hora, segundos en un minuto, etc.).) porque es divisible por un gran conjunto de números.
- Los factores de 60 son 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60.

2. Comprender que las ecuaciones también se pueden factorizar. Al igual que los números, las variables con coeficientes también se pueden factorizar. Lo haces encontrando los factores del coeficiente de la variable. Saber cómo factorizar variables es útil para simplificar ecuaciones de las que forman parte las variables.

3. Aplicar la propiedad distributiva de la multiplicación para factorizar ecuaciones matemáticas. Usando su conocimiento de cómo factorizar números regulares y variables con coeficientes, también puede simplificar las ecuaciones matemáticas al determinar los factores comunes a los números y las variables en una ecuación matemática. Por lo general, simplificaremos la ecuación en la medida de lo posible, buscando el máximo común divisor (mcd). Este proceso de simplificación es posible debido a la propiedad distributiva de la multiplicación, que establece que para cualquier número a, b y c, a(b + c) = ab + ac.
Método 2 de 3: factorización de ecuaciones cuadráticas

1. Asegúrate de que la ecuación esté en forma cuadrática (ax + bx + c = 0). Las ecuaciones cuadráticas son de la forma ax + bx + c = 0, donde a, b y c son constantes numéricas y a no es igual a 0 (tenga en cuenta que a es igual a poder están en 1 o -1). Si está tratando con una ecuación con una variable (x) y uno o más términos de x al cuadrado, generalmente puede intercambiar los términos de la ecuación usando una operación matemática estándar para obtener 0 en un lado de la ecuación. signo y hacha, etc. en la otra mano.
- Por ejemplo, tienes la siguiente ecuación matemática: 5x + 7x - 9 = 4x + x - 18 que se puede simplificar a x + 6x + 9 = 0, en forma cuadrática.
- Ecuaciones con potencias de x más grandes, como x, x, etc. no son ecuaciones cuadráticas. Estas son ecuaciones cúbicas o superiores, a menos que la ecuación se pueda simplificar de manera que se eliminen los términos con potencias de x más altas (que los cuadrados).

2. En ecuaciones cuadráticas donde a = 1, se factoriza en (x+d)(x+e), donde d × e = c y d + e = b. Si su ecuación cuadrática tiene la forma x + bx + c = 0 (en otras palabras, si el coeficiente de x = 1), entonces es posible (pero no seguro) que se pueda usar un atajo relativamente simple para factorizar la ecuación. Encuentre dos números que tengan c como producto y sumarlos para obtener b como una suma. Si tienes estos dos números d y e, ponlos en la siguiente expresión: (x+d)(x+e). Estos dos términos, cuando se multiplican, te dan la ecuación cuadrática; en otras palabras, son los factores de tu ecuación cuadrática.

3. Si es posible, también puede disolver los factores simplemente mirando de cerca. Lo creas o no, puedes resolver ecuaciones cuadráticas simples simplemente observando el problema cuidadosamente y luego sopesando las posibles respuestas hasta que encuentres la correcta. En otras palabras, descomponer en factores probando. Si la ecuación es de la forma ax+bx+c y a>1, entonces los términos serán de la forma (dx +/- _)(ex +/- _), donde d y e son constantes, mayores que cero, que multiplicadas entre sí tienen como producto a. Ambos d y e (o ambos) poder igual a 1, pero esto no siempre es así. Si ambos son 1, entonces esencialmente ha utilizado el método rápido descrito anteriormente.

4. Resuelve esto elevando al cuadrado. En algunos casos, las ecuaciones cuadráticas se pueden factorizar rápida y fácilmente mediante el uso de una propiedad matemática especial. Cualquier ecuación cuadrática de la forma x + 2xh + h = (x + h). Entonces, si en su ecuación el valor de b es el doble de la raíz cuadrada de c, entonces su ecuación puede factorizarse como (x + (sqrt(c))).

5. Usar factores para resolver ecuaciones cuadráticas. Independientemente de cómo factorice una ecuación cuadrática; una vez que se tiene en cuenta, puede encontrar las posibles respuestas para el valor de x igualando cada factor a cero y resolviéndolo. Dado que está buscando valores para x donde su ecuación es cero, un valor para x que haga que cualquiera de los factores sea igual a cero será la posible respuesta de su ecuación cuadrática.

6. Verifique sus respuestas, algunas de ellas pueden ser incorrectas! Una vez que haya encontrado las posibles respuestas para x, vuelva a aplicarlas a su ecuación original para ver si son válidas. A veces las respuestas que encuentras serán la ecuación original no hacer igual a cero cuando los aplicas. estas respuestas son incorrecto y los ignoramos.
Método 3 de 3: factorizar otras formas de ecuaciones

1. Si la ecuación es de la forma a-b, entonces los términos factorizados son (a+b)(a-b). Las ecuaciones de dos variables se resuelven de manera diferente a las ecuaciones cuadráticas. Para cualquier ecuación a-b donde a y b no son iguales a 0, los factores de la ecuación son (a+b)(a-b).
- Por ejemplo, la ecuación 9x - 4y = (3x + 2y)(3x - 2y).

2. Si la ecuación es de la forma a+2ab+b, descomponerla en(a+b). Nota: con a el trinomio de la forma a-2ab+b, la forma disuelta es ligeramente diferente: (a-b).

3. Si la ecuación es de la forma a-b, entonces la descompones en (a-b)(a+ab+b). Finalmente, cabe mencionar que también se pueden factorizar ecuaciones cúbicas y polinomios superiores, aunque este proceso rápidamente se vuelve inviablemente complicado.
Consejos
- a-b se puede factorizar, pero a+b no.
- Aprenda a factorizar constantes: esto puede ayudar.
- Cuidado con las fracciones durante la factorización y resuélvelas correcta y cuidadosamente.
- Si tiene un trinomio de la forma x+bx+ (b/2), entonces la forma factorizada es (x+(b/2)) (puede encontrar esto con una fórmula cuadrada).
- Recuerda que a x 0 = 0.
Artículos de primera necesidad
- Papel
- Lápiz
- Libro de matemáticas (si es necesario)
Artículos sobre el tema. "Factorización de ecuaciones"
Оцените, пожалуйста статью
Popular