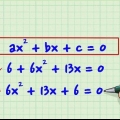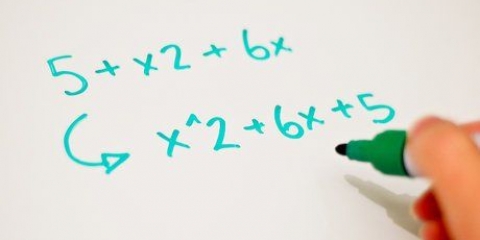→
→ 
 →
→ 
 →
→ 
Observe cómo los signos menos permanecen delante del 2. Cuando se resta un término, el signo menos permanece delante de él. 
Tarea de ejercicio: .
. Factores de 3:1, 3 Factores de 6: 1, 2, 3, 6. `El máximo común divisor es 3`. 
Tarea de ejercicio: .
. Encuentre los máximos comunes divisores: 3 Para eliminar el factor de ambos términos:

Tarea de ejercicio:
Encuentre los máximos comunes divisores: 3 Para eliminar el factor de ambos términos:
Multiplica el factor por la nueva expresión:
Respuesta disuelta final: 

Para reordenar términos:
Encontrar el máximo común divisor:
Para eliminar el factor de ambos términos:
Multiplica el factor por la nueva expresión:
Checar respuesta:


Tarea de ejercicio:
Igual a cero:


Tarea de ejercicio:
Igual a cero:
Disolver:

Tarea de ejercicio:
Igual a cero:
Disolver:
Igualar ambos términos a cero 0: 




y = 0 

y = 4 


 esta respuesta es correcta
esta respuesta es correcta

 Esta respuesta también es correcta.
Esta respuesta también es correcta.

Asignación original:
Para reordenar términos:
Para fusionar términos semejantes:
Encuentre los máximos comunes divisores:
Disolver:

La fórmula para la diferencia de cuadrados perfectos:
Tarea de ejercicio:
Determinar las raíces cuadradas: 

Aplicar raíces cuadradas a la fórmula: 

Fórmula para la diferencia de terceras potencias:
Tarea de ejercicio:
Determinar las raíces cúbicas: ![Factorización de binomios {raíz cuadrada[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factorización de binomios {raíz cuadrada[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Aplicar cubos a la fórmula: 

Fórmula para la suma de cubos perfectos:
Tarea de ejercicio:
Determinar las raíces cúbicas: ![Factorización de binomios {raíz cuadrada[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factorización de binomios {raíz cuadrada[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Aplicar los cubos a la fórmula: 
Factorización de binomios
Contenido
En álgebra, los binomios son expresiones de dos términos conectados por un signo más o menos, como 
Pasos
Parte 1 de 3: factorización de binomios

1. Repasar los conceptos básicos de la factorización de nuevo. Factorizar es dividir un número grande en sus divisores más simples. Cada una de estas partes se llama un `factor`. Por ejemplo, el número 6 es divisible por cuatro números diferentes: 1, 2, 3 y 6. Entonces 1, 2, 3 y 6 son los factores de 6.
- Los factores de 32 son 1, 2, 4, 8, 16 y 32
- Tanto `1` como el número que factorizas son siempre factores. Entonces los factores de un número pequeño como 3 son solo 1 y 3.
- Los factores son solo aquellos números que son completamente divisibles, es decir, los números `enteros`. Podrías dividir 32 por 3.564 o 21.4952, pero esos no son factores, solo números decimales.

2. Haz una lista de los términos del binomio para que sean más fáciles de leer. Un binomio no es más que la suma o resta de dos términos, al menos uno de los cuales contiene una variable. A veces estas variables tienen exponentes, como  o
o  . Si está tratando de factorizar binomios por primera vez, es útil ordenar las ecuaciones en términos de variables descendentes, lo que significa que el exponente más grande viene al final. Por ejemplo:
. Si está tratando de factorizar binomios por primera vez, es útil ordenar las ecuaciones en términos de variables descendentes, lo que significa que el exponente más grande viene al final. Por ejemplo:
 o
o  . Si está tratando de factorizar binomios por primera vez, es útil ordenar las ecuaciones en términos de variables descendentes, lo que significa que el exponente más grande viene al final. Por ejemplo:
. Si está tratando de factorizar binomios por primera vez, es útil ordenar las ecuaciones en términos de variables descendentes, lo que significa que el exponente más grande viene al final. Por ejemplo: →
→ 
 →
→ 
 →
→ 

3. Encuentra el máximo común divisor de ambos términos. Esto significa que estás buscando el número más grande por el que ambas partes del binomio son divisibles. Si esto no funciona, factorice ambos números por sí solos y vea cuál es el número coincidente más alto. Por ejemplo:
 .
.
4. Divide el máximo común divisor de cada término. Si conoces el denominador común, tienes que eliminarlo de cada término. Tenga en cuenta que solo divide los términos, lo que hace que cada uno sea un problema de división más pequeño. Si se hace correctamente, ambas ecuaciones tienen el mismo factor:
 .
.

5. Multiplique su factor por la expresión resultante para redondear. En el último problema sacaste un 3 y obtienes  . Pero no quieres deshacerte de los 3 por completo, solo inclúyelo para simplificar las cosas. No puede simplemente eliminar números sin volver a colocarlos! Multiplica el factor por la expresión para completar esta sección. Por ejemplo:
. Pero no quieres deshacerte de los 3 por completo, solo inclúyelo para simplificar las cosas. No puede simplemente eliminar números sin volver a colocarlos! Multiplica el factor por la expresión para completar esta sección. Por ejemplo:
 . Pero no quieres deshacerte de los 3 por completo, solo inclúyelo para simplificar las cosas. No puede simplemente eliminar números sin volver a colocarlos! Multiplica el factor por la expresión para completar esta sección. Por ejemplo:
. Pero no quieres deshacerte de los 3 por completo, solo inclúyelo para simplificar las cosas. No puede simplemente eliminar números sin volver a colocarlos! Multiplica el factor por la expresión para completar esta sección. Por ejemplo:




6. Verifica tu trabajo multiplicando a la ecuación original. Si hiciste todo bien, es fácil comprobar si lo hiciste bien. Multiplique su factor por los dos términos individuales entre paréntesis. Si coincide con el binomio original dado, entonces lo has hecho bien. De principio a fin resolvemos la expresión  a practicar:
a practicar:
 a practicar:
a practicar:




Parte 2 de 3: Factorización de binomios para resolver ecuaciones

1. Factorizar para simplificar ecuaciones para que sean más fáciles de resolver. Al resolver una ecuación con binomios, especialmente binomios complejos, puede parecer que no hay forma de hacer que todo coincida. Por ejemplo, intenta resolver lo siguiente:  . Una forma de hacer esto, especialmente con exponentes, es factorizar primero.
. Una forma de hacer esto, especialmente con exponentes, es factorizar primero.
 . Una forma de hacer esto, especialmente con exponentes, es factorizar primero.
. Una forma de hacer esto, especialmente con exponentes, es factorizar primero. - Tarea de ejercicio:
- Recuerda que los binomios solo pueden tener dos términos. Si hay más de dos términos, debe aprender a resolver polinomios.

2. Sumar y restar para que un lado de la ecuación sea igual a cero. Toda esta estrategia se basa en uno de los hechos más fundamentales de las matemáticas: algo multiplicado por cero debe ser igual a cero. Entonces, si su ecuación es igual a cero, entonces uno de los términos factorizados debe ser igual a cero! Para empezar, sumarás y restarás para que un lado sea igual a cero.




3. Disuelva el lado distinto de cero como está acostumbrado. En este punto, solo estás fingiendo que el otro lado no existe. Encuentre el máximo común divisor, divídalo y luego cree su expresión factorizada.




4. Establecer los términos dentro y fuera de los paréntesis iguales a cero. En el problema de práctica, multiplicas 2y por (4 – y), y esto debe ser igual a cero. Dado que algo multiplicado por cero es igual a cero, esto significa que 2y o (4 – y) debe ser igual a cero. Haz dos ecuaciones separadas para averiguar qué valor debe tener y para que cualquiera de los lados sea igual a cero.






5. Resolver ambas ecuaciones por cero para la respuesta o respuestas finales. Puede obtener una respuesta o varias respuestas. Recuerda, solo un lado debe ser igual a cero, por lo que puedes obtener algunos valores diferentes para y que resuelvan la misma ecuación. Los últimos pasos de la asignación del ejercicio:





6. Aplique sus respuestas a la ecuación original para asegurarse de que sean correctas. Una vez que haya encontrado los valores correctos para y, debería poder usarlos para resolver la ecuación. Esto es tan simple como probar cada valor de y en lugar de la variable como se muestra a continuación. Las respuestas son y = 0 y y = 4, entonces:


 esta respuesta es correcta
esta respuesta es correcta

 Esta respuesta también es correcta.
Esta respuesta también es correcta.Parte 3 de 3: Lidiar con problemas más difíciles

1. Recuerda que las variables cuentan como factores, incluso con exponentes. Recuerde que la factorización se trata de determinar qué números caben en el número entero. La expresion  es otra forma de decir
es otra forma de decir  . Esto significa que puede colocar cualquier x fuera de los paréntesis si el otro término también tiene uno. Tratar las variables como números regulares. Por ejemplo:
. Esto significa que puede colocar cualquier x fuera de los paréntesis si el otro término también tiene uno. Tratar las variables como números regulares. Por ejemplo:
 es otra forma de decir
es otra forma de decir  . Esto significa que puede colocar cualquier x fuera de los paréntesis si el otro término también tiene uno. Tratar las variables como números regulares. Por ejemplo:
. Esto significa que puede colocar cualquier x fuera de los paréntesis si el otro término también tiene uno. Tratar las variables como números regulares. Por ejemplo: se puede factorizar, porque ambos términos contienen un t. La respuesta final será
- Incluso puede colocar múltiples variables fuera de los paréntesis al mismo tiempo. por ejemplo, en
ambos términos contienen lo mismo
. Puedes disolver esto en

2. Reconocer binomios aún no simplificados combinando términos semejantes. Tomemos, por ejemplo, la expresión  . Aquí parece como si estuvieras tratando con cuatro términos, pero si miras más de cerca te darás cuenta de que solo hay dos. Puede agregar términos similares y dado que tanto 6 como 14 no tienen variable y 2x y 3x comparten la misma variable, se pueden fusionar. Disolver es entonces fácil:
. Aquí parece como si estuvieras tratando con cuatro términos, pero si miras más de cerca te darás cuenta de que solo hay dos. Puede agregar términos similares y dado que tanto 6 como 14 no tienen variable y 2x y 3x comparten la misma variable, se pueden fusionar. Disolver es entonces fácil:
 . Aquí parece como si estuvieras tratando con cuatro términos, pero si miras más de cerca te darás cuenta de que solo hay dos. Puede agregar términos similares y dado que tanto 6 como 14 no tienen variable y 2x y 3x comparten la misma variable, se pueden fusionar. Disolver es entonces fácil:
. Aquí parece como si estuvieras tratando con cuatro términos, pero si miras más de cerca te darás cuenta de que solo hay dos. Puede agregar términos similares y dado que tanto 6 como 14 no tienen variable y 2x y 3x comparten la misma variable, se pueden fusionar. Disolver es entonces fácil:





3. Reconocer la especial `diferencia de cuadrados perfectos`. Un cuadrado perfecto es un número cuya raíz es un número entero, como 
 ,
, 
 , o incluso
, o incluso 
 Si tu binomio es una suma menos con dos cuadrados perfectos, como
Si tu binomio es una suma menos con dos cuadrados perfectos, como  , entonces puedes usarlos en esta fórmula:
, entonces puedes usarlos en esta fórmula:

 ,
, 
 , o incluso
, o incluso 
 Si tu binomio es una suma menos con dos cuadrados perfectos, como
Si tu binomio es una suma menos con dos cuadrados perfectos, como  , entonces puedes usarlos en esta fórmula:
, entonces puedes usarlos en esta fórmula:





4. Aprende a simplificar la `diferencia de cubos perfectos`. Al igual que los cuadrados perfectos, esta es una fórmula simple donde dos cubos se restan entre sí. Por ejemplo,  . Como antes, encuentra la raíz cúbica de cada uno y utilízala en la fórmula:
. Como antes, encuentra la raíz cúbica de cada uno y utilízala en la fórmula:
 . Como antes, encuentra la raíz cúbica de cada uno y utilízala en la fórmula:
. Como antes, encuentra la raíz cúbica de cada uno y utilízala en la fórmula:

![Factorización de binomios {raíz cuadrada[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factorización de binomios {raíz cuadrada[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)


5. Saber que la suma de cubos perfectos también encaja en una fórmula. A diferencia de la diferencia de cuadrados perfectos, puedes usar cubos agregados, como  , también fácil de encontrar con una fórmula simple. Esto es casi exactamente lo mismo que el anterior, pero con algunas ventajas y desventajas invertidas. La fórmula es tan fácil como las otras dos, y todo lo que tienes que hacer es reconocer los dos cubos en el problema:
, también fácil de encontrar con una fórmula simple. Esto es casi exactamente lo mismo que el anterior, pero con algunas ventajas y desventajas invertidas. La fórmula es tan fácil como las otras dos, y todo lo que tienes que hacer es reconocer los dos cubos en el problema:
 , también fácil de encontrar con una fórmula simple. Esto es casi exactamente lo mismo que el anterior, pero con algunas ventajas y desventajas invertidas. La fórmula es tan fácil como las otras dos, y todo lo que tienes que hacer es reconocer los dos cubos en el problema:
, también fácil de encontrar con una fórmula simple. Esto es casi exactamente lo mismo que el anterior, pero con algunas ventajas y desventajas invertidas. La fórmula es tan fácil como las otras dos, y todo lo que tienes que hacer es reconocer los dos cubos en el problema:

![Factorización de binomios {raíz cuadrada[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factorización de binomios {raíz cuadrada[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)

Consejos
- No todos los binomios tienen divisores comunes! Algunos ya se han simplificado tanto como sea posible.
- Si no está seguro de si hay un divisor común, primero divida por números más pequeños. Por ejemplo, si no ve de inmediato que 16 es el divisor común de 32 y 16, comience a dividir ambos números por 2. Esto deja 16 y 8, que también se puede dividir por 8. Ahora tienes 2 y 1, los factores más pequeños. Claramente hay un divisor común mayor que 8 y 2.
- Tenga en cuenta que una sexta potencia (x) es un cuadrado perfecto y es un cubo perfecto. Por lo tanto, puede aplicar cualquiera de las fórmulas especiales anteriores, en cualquier orden, a un binomio que es la diferencia de sextas potencias perfectas, como x - 64. Sin embargo, puede que le resulte más fácil aplicar primero la fórmula de la diferencia para cuadrados perfectos para que pueda factorizar aún más el binomio.
Advertencias
- Un binomio que es la suma de cuadrados perfectos no se puede factorizar.
Artículos sobre el tema. "Factorización de binomios"
Оцените, пожалуйста статью
Popular