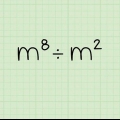Diez a la potencia de tres











Como se muestra aquí, puede continuar multiplicando la base por el producto de cada uno de los primeros pares de números hasta obtener la respuesta final. Sigue multiplicando los primeros dos números, luego multiplica esta respuesta por el siguiente número en la secuencia. Esto es cierto para cualquier exponente. Cuando haya terminado con el ejemplo, obtendrá  .
. 




Utilice un motor de búsqueda como Startpage, Duckduckgo o Google para encontrar la respuesta. Puede usar el botón `^` en su computadora, tableta o teléfono inteligente para ingresar la expresión en el cuadro de búsqueda, e inmediatamente verá la respuesta y sugerencias para explorar expresiones similares (Duckduckgo incluso muestra una calculadora completa). 





Como todo es el mismo número, pero multiplicado, podemos combinar estos: 




Como las bases son las mismas, puedes simplemente sumarlas: 




Como verás en un momento, cualquier número que sea parte de una fracción, como  , ser reescrito como
, ser reescrito como  . Los exponentes negativos forman fracciones.
. Los exponentes negativos forman fracciones. 
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Recuerda que un número sin potencia tiene un exponente de 1
Recuerda que un número sin potencia tiene un exponente de 1 =
= 
 =
= 




![Resolución de exponentes x^{{{frac{1}{3}}}}={raíz cuadrada[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Resolución de exponentes ({raíz cuadrada[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)



Resolución de exponentes
Contenido
Los exponentes se utilizan cuando un número se multiplica por sí mismo. En vez de 



Pasos
Método 1 de 3: resolver exponentes simples

1. Aprende los términos y el vocabulario correctos para problemas exponenciales. ¿Tienes un exponente como  , entonces trabajas con dos partes simples. El número de chasis aquí es un 2, o el base. Este número se eleva a la potencia de 3, también conocido como el exponente o energía. ¿estamos hablando de
, entonces trabajas con dos partes simples. El número de chasis aquí es un 2, o el base. Este número se eleva a la potencia de 3, también conocido como el exponente o energía. ¿estamos hablando de  , entonces decimos `dos a la tercera`, `dos a la tercera potencia`, o `dos elevados a la tercera potencia`.`
, entonces decimos `dos a la tercera`, `dos a la tercera potencia`, o `dos elevados a la tercera potencia`.`
 , entonces trabajas con dos partes simples. El número de chasis aquí es un 2, o el base. Este número se eleva a la potencia de 3, también conocido como el exponente o energía. ¿estamos hablando de
, entonces trabajas con dos partes simples. El número de chasis aquí es un 2, o el base. Este número se eleva a la potencia de 3, también conocido como el exponente o energía. ¿estamos hablando de  , entonces decimos `dos a la tercera`, `dos a la tercera potencia`, o `dos elevados a la tercera potencia`.`
, entonces decimos `dos a la tercera`, `dos a la tercera potencia`, o `dos elevados a la tercera potencia`.` - Si un número se eleva a la segunda potencia, como
, entonces también puedes decir que el número es al cuadrado es, como `cinco al cuadrado.`
- Si un número se eleva a la tercera potencia, como
, entonces también puedes decir ese número a número de cubo es.
- Si se menciona un número sin exponente, como 4, por ejemplo, entonces teóricamente está en la primera potencia y se puede reescribir como
.
- Si el exponente es igual a 0, y un `número (distinto de cero)` se eleva a la `potencia cero`, entonces el entero es igual a 1, como
o incluso algo como
Más sobre esto en la sección `Consejos`.

2. Multiplica la base el número de veces por sí mismo como lo indica el exponente. Si tienes que resolver una potencia a mano, empiezas reescribiéndola como una multiplicación. Multiplicas la base el número de veces por sí mismo, como lo indica el exponente. Y tu tambien  luego multiplicas tres por cuatro por si mismo
luego multiplicas tres por cuatro por si mismo  . Algunos ejemplos más son:
. Algunos ejemplos más son:
 luego multiplicas tres por cuatro por si mismo
luego multiplicas tres por cuatro por si mismo  . Algunos ejemplos más son:
. Algunos ejemplos más son:



3. Resuelve una expresión: Multiplica los dos primeros números para obtener el producto. Por ejemplo, con  , empiezas con
, empiezas con  Esto parece una tarea tediosa, pero hazlo paso a paso. Comience multiplicando los primeros dos cuatros. Luego reemplace los dos cuatros con la respuesta como se muestra a continuación:
Esto parece una tarea tediosa, pero hazlo paso a paso. Comience multiplicando los primeros dos cuatros. Luego reemplace los dos cuatros con la respuesta como se muestra a continuación:
 , empiezas con
, empiezas con  Esto parece una tarea tediosa, pero hazlo paso a paso. Comience multiplicando los primeros dos cuatros. Luego reemplace los dos cuatros con la respuesta como se muestra a continuación:
Esto parece una tarea tediosa, pero hazlo paso a paso. Comience multiplicando los primeros dos cuatros. Luego reemplace los dos cuatros con la respuesta como se muestra a continuación:



4. Multiplica la respuesta del primer par (16) por el siguiente número. Sigue multiplicando los números para `crecer` tu exponente. Siguiendo con nuestro ejemplo, multiplicamos 16 por los siguientes 4 de forma que:






 .
.
5. Pruebe también los siguientes ejemplos y verifique sus respuestas con una calculadora.




6. Utilice el `exp`, `X norte  botón ` o `^` de su calculadora para los exponentes. Es casi imposible encontrar exponentes más grandes, como
botón ` o `^` de su calculadora para los exponentes. Es casi imposible encontrar exponentes más grandes, como  a mano, pero las calculadoras pueden manejar esto fácilmente. El botón para esto generalmente se indica con suficiente claridad. La calculadora de Windows se puede expandir a una calculadora científica haciendo clic en la pestaña `Ver` de la calculadora y seleccionando `Científica`. Si desea recuperar la calculadora predeterminada, haga clic en `Ver` nuevamente y seleccione `Predeterminado`.
a mano, pero las calculadoras pueden manejar esto fácilmente. El botón para esto generalmente se indica con suficiente claridad. La calculadora de Windows se puede expandir a una calculadora científica haciendo clic en la pestaña `Ver` de la calculadora y seleccionando `Científica`. Si desea recuperar la calculadora predeterminada, haga clic en `Ver` nuevamente y seleccione `Predeterminado`.
 botón ` o `^` de su calculadora para los exponentes. Es casi imposible encontrar exponentes más grandes, como
botón ` o `^` de su calculadora para los exponentes. Es casi imposible encontrar exponentes más grandes, como  a mano, pero las calculadoras pueden manejar esto fácilmente. El botón para esto generalmente se indica con suficiente claridad. La calculadora de Windows se puede expandir a una calculadora científica haciendo clic en la pestaña `Ver` de la calculadora y seleccionando `Científica`. Si desea recuperar la calculadora predeterminada, haga clic en `Ver` nuevamente y seleccione `Predeterminado`.
a mano, pero las calculadoras pueden manejar esto fácilmente. El botón para esto generalmente se indica con suficiente claridad. La calculadora de Windows se puede expandir a una calculadora científica haciendo clic en la pestaña `Ver` de la calculadora y seleccionando `Científica`. Si desea recuperar la calculadora predeterminada, haga clic en `Ver` nuevamente y seleccione `Predeterminado`.Método 2 de 3: sumar, restar y multiplicar exponentes

1. Solo puedes sumar o restar números de potencia entre sí si tienen la misma base y el mismo exponente. Si se trata de bases y exponentes idénticos, como  , entonces puedes simplificar la suma de los términos a una multiplicación. No olvides eso
, entonces puedes simplificar la suma de los términos a una multiplicación. No olvides eso  puede ser considerado como
puede ser considerado como  , de modo que
, de modo que  agregando, donde `1 de eso + 1 de eso = 2 de eso`, cualquiera que sea `eso`. Simplemente sume el número de términos semejantes (aquellos con la misma base y exponente) y multiplique la suma por esa expresión exponencial. entonces puedes
agregando, donde `1 de eso + 1 de eso = 2 de eso`, cualquiera que sea `eso`. Simplemente sume el número de términos semejantes (aquellos con la misma base y exponente) y multiplique la suma por esa expresión exponencial. entonces puedes  resuelve y multiplica esa respuesta por dos. Recuerda que esto es posible porque una multiplicación no es más que reescribir una suma, porque
resuelve y multiplica esa respuesta por dos. Recuerda que esto es posible porque una multiplicación no es más que reescribir una suma, porque  . Aquí están algunos ejemplos:
. Aquí están algunos ejemplos:
 , entonces puedes simplificar la suma de los términos a una multiplicación. No olvides eso
, entonces puedes simplificar la suma de los términos a una multiplicación. No olvides eso  puede ser considerado como
puede ser considerado como  , de modo que
, de modo que  agregando, donde `1 de eso + 1 de eso = 2 de eso`, cualquiera que sea `eso`. Simplemente sume el número de términos semejantes (aquellos con la misma base y exponente) y multiplique la suma por esa expresión exponencial. entonces puedes
agregando, donde `1 de eso + 1 de eso = 2 de eso`, cualquiera que sea `eso`. Simplemente sume el número de términos semejantes (aquellos con la misma base y exponente) y multiplique la suma por esa expresión exponencial. entonces puedes  resuelve y multiplica esa respuesta por dos. Recuerda que esto es posible porque una multiplicación no es más que reescribir una suma, porque
resuelve y multiplica esa respuesta por dos. Recuerda que esto es posible porque una multiplicación no es más que reescribir una suma, porque  . Aquí están algunos ejemplos:
. Aquí están algunos ejemplos: 
2. Multiplica números con la misma base sumando los exponentes. Si tienes dos exponentes con la misma base, como  , entonces solo necesitas sumar los dos exponentes con la misma base. Entonces,
, entonces solo necesitas sumar los dos exponentes con la misma base. Entonces, . Si encuentra esto un poco extraño, divídalo en partes más pequeñas para comprender cómo funciona el sistema:
. Si encuentra esto un poco extraño, divídalo en partes más pequeñas para comprender cómo funciona el sistema:
 , entonces solo necesitas sumar los dos exponentes con la misma base. Entonces,
, entonces solo necesitas sumar los dos exponentes con la misma base. Entonces, . Si encuentra esto un poco extraño, divídalo en partes más pequeñas para comprender cómo funciona el sistema:
. Si encuentra esto un poco extraño, divídalo en partes más pequeñas para comprender cómo funciona el sistema:






3. Multiplicar un número exponencial elevado a otra potencia, como ( X 2 ) 5  . Si elevas un número a cierta potencia, y el entero se eleva a cierta potencia, solo multiplicas los dos exponentes. Entonces,
. Si elevas un número a cierta potencia, y el entero se eleva a cierta potencia, solo multiplicas los dos exponentes. Entonces,  . Si te confundes, piensa de nuevo qué significan realmente estos símbolos.
. Si te confundes, piensa de nuevo qué significan realmente estos símbolos.  solo significa tu
solo significa tu  Multiplica 5 veces por sí mismo, entonces:
Multiplica 5 veces por sí mismo, entonces:
 . Si elevas un número a cierta potencia, y el entero se eleva a cierta potencia, solo multiplicas los dos exponentes. Entonces,
. Si elevas un número a cierta potencia, y el entero se eleva a cierta potencia, solo multiplicas los dos exponentes. Entonces,  . Si te confundes, piensa de nuevo qué significan realmente estos símbolos.
. Si te confundes, piensa de nuevo qué significan realmente estos símbolos.  solo significa tu
solo significa tu  Multiplica 5 veces por sí mismo, entonces:
Multiplica 5 veces por sí mismo, entonces:



4. Piense en los exponentes negativos como fracciones, o el recíproco del número. No sé qué es un recíproco, no hay problema. Si se trata de un exponente negativo, como  , luego haga que el exponente sea positivo y colóquelo como denominador debajo de uno, lo que da como resultado
, luego haga que el exponente sea positivo y colóquelo como denominador debajo de uno, lo que da como resultado  . Aquí hay algunos ejemplos adicionales:
. Aquí hay algunos ejemplos adicionales:
 , luego haga que el exponente sea positivo y colóquelo como denominador debajo de uno, lo que da como resultado
, luego haga que el exponente sea positivo y colóquelo como denominador debajo de uno, lo que da como resultado  . Aquí hay algunos ejemplos adicionales:
. Aquí hay algunos ejemplos adicionales:


5. Dividir dos números con la misma base restando los exponentes. La división es lo opuesto a la multiplicación, y aunque no se resuelven exactamente como opuestos, están aquí. Si se trata de la ecuación  , simplemente reste el exponente superior del inferior y deje la base como está. Entonces,
, simplemente reste el exponente superior del inferior y deje la base como está. Entonces,  , o dieciséis.
, o dieciséis.
 , simplemente reste el exponente superior del inferior y deje la base como está. Entonces,
, simplemente reste el exponente superior del inferior y deje la base como está. Entonces,  , o dieciséis.
, o dieciséis. , ser reescrito como
, ser reescrito como  . Los exponentes negativos forman fracciones.
. Los exponentes negativos forman fracciones.
6. Pruebe algunos ejercicios de práctica para acostumbrarse a trabajar con números de potencia. Los siguientes ejercicios practican todo lo discutido hasta ahora. Para la respuesta, simplemente seleccione la línea que contiene el problema.
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Recuerda que un número sin potencia tiene un exponente de 1
Recuerda que un número sin potencia tiene un exponente de 1 =
= 
 =
= 
Método 3 de 3: resolver fracciones como números de potencia

1. Trata las fracciones en forma de números de potencia, como X 1 2  como raíz cuadrada.
como raíz cuadrada.  de hecho es exactamente lo mismo que
de hecho es exactamente lo mismo que  . Esto es cierto independientemente del denominador de la fracción, por lo que
. Esto es cierto independientemente del denominador de la fracción, por lo que  se convierte en la raíz cuadrática de x, también escrita como
se convierte en la raíz cuadrática de x, también escrita como ![Resolución de exponentes {raíz cuadrada[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
.
 como raíz cuadrada.
como raíz cuadrada.  de hecho es exactamente lo mismo que
de hecho es exactamente lo mismo que  . Esto es cierto independientemente del denominador de la fracción, por lo que
. Esto es cierto independientemente del denominador de la fracción, por lo que  se convierte en la raíz cuadrática de x, también escrita como
se convierte en la raíz cuadrática de x, también escrita como ![Resolución de exponentes {raíz cuadrada[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
. - Las raíces son el inverso de los exponentes. Por ejemplo, si toma la respuesta de
a la cuarta potencia, luego vuelves a
, y también puede
también se escribe como
. Otro ejemplo es
y luego
y por lo tanto
.

2. Haz que el numerador sea un exponente normal para una fracción mixta. puede parecer imposible, pero es fácil si recuerdas cómo se multiplican los exponentes. Haga que la base sea una raíz cuadrada, como una fracción normal, y eleve todo a la potencia en la parte superior de la fracción. Si le resulta difícil recordar esto, vuelva a repasar la teoría. Al final eso se aplica
puede parecer imposible, pero es fácil si recuerdas cómo se multiplican los exponentes. Haga que la base sea una raíz cuadrada, como una fracción normal, y eleve todo a la potencia en la parte superior de la fracción. Si le resulta difícil recordar esto, vuelva a repasar la teoría. Al final eso se aplica  simplemente es igual
simplemente es igual  Por ejemplo:
Por ejemplo:
 puede parecer imposible, pero es fácil si recuerdas cómo se multiplican los exponentes. Haga que la base sea una raíz cuadrada, como una fracción normal, y eleve todo a la potencia en la parte superior de la fracción. Si le resulta difícil recordar esto, vuelva a repasar la teoría. Al final eso se aplica
puede parecer imposible, pero es fácil si recuerdas cómo se multiplican los exponentes. Haga que la base sea una raíz cuadrada, como una fracción normal, y eleve todo a la potencia en la parte superior de la fracción. Si le resulta difícil recordar esto, vuelva a repasar la teoría. Al final eso se aplica  simplemente es igual
simplemente es igual  Por ejemplo:
Por ejemplo:

![Resolución de exponentes x^{{{frac{1}{3}}}}={raíz cuadrada[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Resolución de exponentes ({raíz cuadrada[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)

3. Puede sumar, restar y multiplicar fracciones en forma de números de potencia, tal como lo haría normalmente. Es mucho más fácil sumar o restar los exponentes antes de resolverlos o convertirlos a raíces cuadradas. Si la base es la misma y el exponente es el mismo, entonces puedes sumarlos y restarlos. Si solo la base es la misma, entonces puedes multiplicar y dividir los exponentes como de costumbre, siempre y cuando tengas en cuenta como sumar y restar fracciones. Por ejemplo:


Consejos
- La mayoría de las calculadoras tienen un botón para exponentes, presione después de ingresar la base, para resolver problemas de números de potencia.Por lo general, esto se ve como un ^ o x^y.
- `Simplificar` en matemáticas significa haga las ediciones necesarias para obtener la forma más simple de las expresiones en cuestión.
- 1 es el elemento de identidad de los exponentes. Eso significa que cualquier número real elevado a la potencia de 1 (a la primera potencia) es el número mismo, por ejemplo:
Además, 1 es el elemento de identidad de la multiplicación (1 como multiplicador, como
), y de la división (1 como dividendo, como
.
- La base cero a cero (0) no está definida (inglés: dne, no existe). Las computadoras o calculadoras devolverán un `error`. Recuerda que cualquier número distinto de cero elevado a la potencia 0 siempre es igual a 1,
- Por ejemplo, las matemáticas superiores para números imaginarios son,
, por lo cual
; e es una constante continua irracional igual a 2.71828..., y a es una constante arbitraria. La prueba se puede encontrar en la mayoría de los libros de matemáticas superiores.
Advertencias
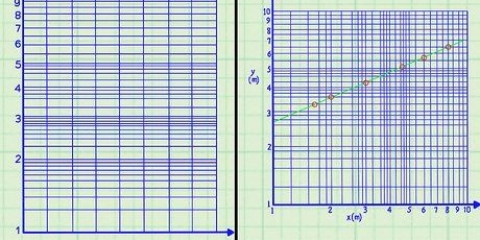
- Un aumento exponencial hace que el producto suba cada vez más rápido, por lo que la respuesta puede parecer incorrecta, cuando es correcta. (Compruebe esto graficando una función exponencial, por ejemplo.: 2, si x tiene un rango de valores diferentes).
Artículos sobre el tema. "Resolución de exponentes"
Оцените, пожалуйста статью
Similar
Popular