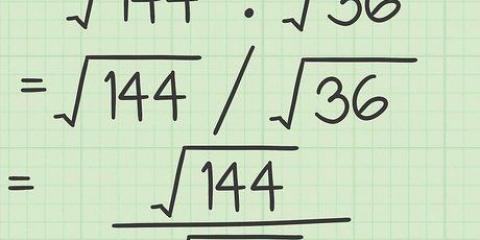Ejemplo 1: Resuelve:  .
.
Comience por convertir esto a un logaritmo usando la fórmula anterior: .
. Esta fórmula es la fórmula de `cambio de base`, derivada de las propiedades logarítmicas básicas. 
Ejemplo 1 (continuación.): Volver a escribir  Si
Si  . El valor de `?` es la respuesta al problema. Puede que tengas que probar algunos para encontrarlo:
. El valor de `?` es la respuesta al problema. Puede que tengas que probar algunos para encontrarlo:



16 es lo que estabas buscando, así que = 4.
= 4. 
Ejemplo 2: ¿Qué es  ?
? Convierte esto a un logaritmo::  .(Tenga en cuenta que el 3 desaparece en cualquier registro inicial; esto se aplica a cualquier base).
.(Tenga en cuenta que el 3 desaparece en cualquier registro inicial; esto se aplica a cualquier base). Reescribir como  y probar posibles valores de ?:
y probar posibles valores de ?:


Como 58 cae entre estos dos números, ningún entero como respuesta.
ningún entero como respuesta. Deja tu respuesta como:  .
. 

si x o y es negativo, no hay solución al problema. Si ambos x si y son negativos, elimine los signos negativos usando la propiedad 
No hay logaritmos de números negativos en el problema de ejemplo, por lo que puede continuar con el siguiente paso. 
Use esto para expandir el lado izquierdo del problema de muestra:

Sustituye esto de nuevo en la ecuación original:

→


El problema de ejemplo tiene un nuevo término:  . Como 3 = 27, simplifica
. Como 3 = 27, simplifica  desagradable 3.
desagradable 3. La comparación completa es ahora:




 .
.
En el problema de ejemplo, el norte todavía atrapado en el término  .
.
Alrededor de norte para aislar, use la regla del producto de logaritmos:

Vuelva a sustituir esto en la ecuación completa:





Dado que 3 = 19683, n =19683
Compartir logaritmos
Contenido
Los logaritmos pueden parecer difíciles de usar, pero al igual que los exponentes o los polinomios, solo tienes que aprender las técnicas correctas. Solo necesitas saber algunas propiedades básicas para dividir dos logaritmos con la misma base, o extender un logaritmo por un cociente.
Pasos
Método 1 de 2: dividir logaritmos a mano

1. Comprobar números negativos y unos. Este método trata problemas en la forma  . Sin embargo, no funciona para algunos casos especiales:
. Sin embargo, no funciona para algunos casos especiales:
 . Sin embargo, no funciona para algunos casos especiales:
. Sin embargo, no funciona para algunos casos especiales: - El logaritmo de un número negativo no está definido para todas las bases (como
o
). Luego escribe `Sin solución`.
- El logaritmo del cero tampoco está definido para todas las bases. Si ves un término como
, luego también escriba `Sin solución`.
- El logaritmo de uno en cualquier base (
) siempre es igual a cero, ya que
para todos los valores de X. Reemplace ese logaritmo con 1 en lugar de usar el método a continuación.
- Si los dos logaritmos tienen bases diferentes, como
, y no puede simplificar ninguno de ellos a un número entero, entonces el problema no se puede resolver a mano.

2. Edite la expresión en un logaritmo. Suponiendo que no encontró ninguna de las excepciones anteriores, ahora puede simplificar el problema en un logaritmo. Para ello, utilice la fórmula .
.
 .
. .
.Comience por convertir esto a un logaritmo usando la fórmula anterior:
 .
.
3. Calcula esto a mano si es posible. Recuerda: om  para resolver, piensas en `
para resolver, piensas en ` ` o `¿Qué exponente puedo usar? a elevar a X Llegar?No siempre es posible resolver esto sin una calculadora, pero si tienes suerte terminarás con un logaritmo fácilmente simplificado.
` o `¿Qué exponente puedo usar? a elevar a X Llegar?No siempre es posible resolver esto sin una calculadora, pero si tienes suerte terminarás con un logaritmo fácilmente simplificado.
 para resolver, piensas en `
para resolver, piensas en ` ` o `¿Qué exponente puedo usar? a elevar a X Llegar?No siempre es posible resolver esto sin una calculadora, pero si tienes suerte terminarás con un logaritmo fácilmente simplificado.
` o `¿Qué exponente puedo usar? a elevar a X Llegar?No siempre es posible resolver esto sin una calculadora, pero si tienes suerte terminarás con un logaritmo fácilmente simplificado. Si
Si  . El valor de `?` es la respuesta al problema. Puede que tengas que probar algunos para encontrarlo:
. El valor de `?` es la respuesta al problema. Puede que tengas que probar algunos para encontrarlo:


16 es lo que estabas buscando, así que
 = 4.
= 4.
4. Deje la respuesta en forma de logaritmo si no puede simplificarla. Algunos logaritmos son muy difíciles de resolver a mano. Necesitas una calculadora si necesitas la respuesta para un propósito práctico. Cuando resuelves problemas en la clase de matemáticas, tu profesor probablemente espera que dejes la respuesta como logaritmo. Aquí hay otro ejemplo que usa este método para un problema más complicado:
 ?
? .(Tenga en cuenta que el 3 desaparece en cualquier registro inicial; esto se aplica a cualquier base).
.(Tenga en cuenta que el 3 desaparece en cualquier registro inicial; esto se aplica a cualquier base). y probar posibles valores de ?:
y probar posibles valores de ?:

Como 58 cae entre estos dos números,
 ningún entero como respuesta.
ningún entero como respuesta. .
.Método 2 de 2: trabajar con el logaritmo de un cociente

1. Comience con un problema de división en un logaritmo. Esta sección te ayuda a resolver problemas con expresiones en la forma  .
.
 .
. - Por ejemplo, comience con este problema:
`Resolver para n si.`

2. Comprobar números negativos. El logaritmo de un número negativo no está definido. Si x o y son un número negativo, verifica si el problema tiene solución antes de continuar:


3. Divide el cociente en dos logaritmos. Una propiedad útil de los logaritmos se describe mediante la fórmula:  . En otras palabras, el logaritmo de un cociente siempre es igual al logaritmo del numerador, menos el logaritmo del denominador.
. En otras palabras, el logaritmo de un cociente siempre es igual al logaritmo del numerador, menos el logaritmo del denominador.
 . En otras palabras, el logaritmo de un cociente siempre es igual al logaritmo del numerador, menos el logaritmo del denominador.
. En otras palabras, el logaritmo de un cociente siempre es igual al logaritmo del numerador, menos el logaritmo del denominador.

→


4. Simplifique los logaritmos si es posible. Si alguno de los nuevos logaritmos en la expresión es un número entero, simplificarlos ahora.
 . Como 3 = 27, simplifica
. Como 3 = 27, simplifica  desagradable 3.
desagradable 3.

5. Aislar la variable. Como cualquier problema matemático, ayuda aislar el término con la variable en un lado de la ecuación. Eliminar términos semejantes donde sea posible para simplificar la ecuación.


 .
.
6. Use propiedades adicionales de logaritmos cuando sea necesario. Para aislar la variable de otros términos dentro del mismo logaritmo, reescriba el término usando diferentes propiedades logarítmicas.
 .
.Alrededor de norte para aislar, use la regla del producto de logaritmos:





7. Sigue simplificando hasta que encuentres la solución. Repita las mismas técnicas algebraicas y logarítmicas para resolver el problema. Si no hay una solución entera, use una calculadora y redondear al número significativo más cercano.


Dado que 3 = 19683, n =19683
Artículos sobre el tema. "Compartir logaritmos"
Оцените, пожалуйста статью
Similar
Popular