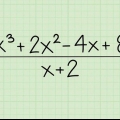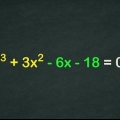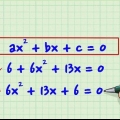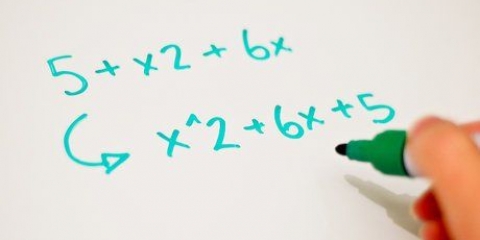Por ejemplo, 

por ejemplo, a  en
en  para aislar, tiras
para aislar, tiras  de ambos lados de la ecuación la ecuación:
de ambos lados de la ecuación la ecuación:




por ejemplo, a  para ser resuelto en
para ser resuelto en  , dividir cada lado de la ecuación por
, dividir cada lado de la ecuación por  :
:



Entonces la solución de es es
es  .
. 

Por ejemplo, reescribir  Así que si
Así que si  .
. 
Por ejemplo,  .
. 
Por ejemplo, para el polinomio cuadrático  , necesitas encontrar dos números (
, necesitas encontrar dos números ( y
y  ), cierto
), cierto  y
y  .
. Porque tú  sabes que uno de los números será negativo.
sabes que uno de los números será negativo. deberías ver eso  y
y  . Entonces te separas
. Entonces te separas  en en
en en  y reescribir el polinomio cuadrático:
y reescribir el polinomio cuadrático:  .
. 
Por ejemplo, los dos primeros términos del polinomio  son
son  . Un término que ocurre en ambos es
. Un término que ocurre en ambos es  . Esto se convierte en el grupo disuelto
. Esto se convierte en el grupo disuelto  .
. 
Por ejemplo, los dos segundos términos del polinomio  son
son  . Un término que ocurre en ambos es
. Un término que ocurre en ambos es  . Así es el grupo disuelto
. Así es el grupo disuelto  .
. 
Por ejemplo, después de factorizar por agrupación, .se convierte en  igual a
igual a  .
. El primer binomio es  .
. El segundo binomio es  .
. Así que el polinomio cuadrático original,  se puede escribir como la expresión factorizada
se puede escribir como la expresión factorizada  .
. 
Por ejemplo, para encontrar la primera solución de  , igualar la primera expresión binomial a
, igualar la primera expresión binomial a  y perderte
y perderte  sobre. Por lo tanto:
sobre. Por lo tanto:



Entonces, la primera solución del polinomio cuadrático es
es  .
. 
Por ejemplo, para encontrar la segunda solución para  , igualar la segunda expresión binomial a
, igualar la segunda expresión binomial a  y perderte
y perderte  sobre. Por lo tanto:
sobre. Por lo tanto:



Entonces la segunda solución del polinomio cuadrático es igual a
igual a  .
.
Resuelve polinomios
Contenido
Un polinomio es una expresión formada por sumas y restas de términos. Un término puede constar de variables, constantes y coeficientes. Cuando resuelves polinomios, generalmente tratas de averiguar para qué puntos x = 0. Los polinomios de menor grado tienen una o dos soluciones, dependiendo de si son polinomios lineales o polinomios cuadráticos. Estos tipos de polinomios se pueden resolver fácilmente usando álgebra elemental y factorización. Para resolver polinomios de mayor grado, puedes leer artículos en wikiHow.
Pasos
Método 1 de 2: resolver un polinomio lineal

1. Determina si estás tratando con un polinomio lineal. Un polinomio lineal es un polinomio de primer grado. Esto significa que ninguna variable tendrá un exponente (o un exponente mayor que 1). Como este es un polinomio de primer grado, tiene exactamente una solución.
- Por ejemplo,
es un polinomio lineal (o polinomio), porque la variable
no tiene exponente (que es lo mismo que un exponente de 1).

2. Hacer la ecuación igual a cero. Este es un paso necesario para resolver todos los polinomios.


3. Mover el término variable a un lado. Haz esto sumando o restando la constante de ambos lados de la ecuación. Una constante es un término sin variable.
 en
en  para aislar, tiras
para aislar, tiras  de ambos lados de la ecuación la ecuación:
de ambos lados de la ecuación la ecuación:



4. Resuelve la variable. Usualmente tienes que dividir cada lado de la ecuación por la constante. Esto te da la solución del polinomio.
 para ser resuelto en
para ser resuelto en  , dividir cada lado de la ecuación por
, dividir cada lado de la ecuación por  :
:


Entonces la solución de es
 es
es  .
.Método 2 de 2: resolver un polinomio cuadrático

1. Determine si se trata de un polinomio cuadrático. Un polinomio cuadrático es una ecuación cuadrática. Esto significa que ninguna variable tiene un exponente mayor que 2. Como este es un polinomio de segundo grado, hay dos soluciones.
- Por ejemplo,
es un polinomio cuadrático, porque la variable
a
tiene como exponente.

2. Asegúrate de que el polinomio esté escrito en orden de grado. Esto significa que el término con exponente  aparece primero seguido del término de primer grado, luego la constante.
aparece primero seguido del término de primer grado, luego la constante.
 aparece primero seguido del término de primer grado, luego la constante.
aparece primero seguido del término de primer grado, luego la constante. Así que si
Así que si  .
.
3. Hacer la ecuación igual a cero. Este es un paso necesario para resolver todos los polinomios.
 .
.
4. Reescribe la expresión como una expresión de cuatro términos. Esto se hace dividiendo el término de primer grado (de  término). Estás buscando dos números cuya suma sea igual al coeficiente de primer grado y cuyo producto sea igual a la constante.
término). Estás buscando dos números cuya suma sea igual al coeficiente de primer grado y cuyo producto sea igual a la constante.
 término). Estás buscando dos números cuya suma sea igual al coeficiente de primer grado y cuyo producto sea igual a la constante.
término). Estás buscando dos números cuya suma sea igual al coeficiente de primer grado y cuyo producto sea igual a la constante. , necesitas encontrar dos números (
, necesitas encontrar dos números ( y
y  ), cierto
), cierto  y
y  .
. sabes que uno de los números será negativo.
sabes que uno de los números será negativo. y
y  . Entonces te separas
. Entonces te separas  en en
en en  y reescribir el polinomio cuadrático:
y reescribir el polinomio cuadrático:  .
.
5. Factorizar por agrupación. Lo haces factorizando un término que coincida con las dos primeras condiciones en el polinomio.
 son
son  . Un término que ocurre en ambos es
. Un término que ocurre en ambos es  . Esto se convierte en el grupo disuelto
. Esto se convierte en el grupo disuelto  .
.
6. factoriza el segundo grupo. Haces esto al factorizar un término que ocurre en los segundos dos términos del polinomio.
 son
son  . Un término que ocurre en ambos es
. Un término que ocurre en ambos es  . Así es el grupo disuelto
. Así es el grupo disuelto  .
.
7. Reescribe el polinomio como dos binomios. Un binomio es una expresión con dos términos. Ya tienes un binomio, la expresión entre paréntesis para cada grupo. Esta expresión debe ser la misma para todos los grupos. El segundo binomio se forma combinando los dos términos factorizados de cada grupo.
 igual a
igual a  .
. .
. .
. se puede escribir como la expresión factorizada
se puede escribir como la expresión factorizada  .
.
8. Encuentre la solución primero. Lo haces resolviendo  en el primer binomio.
en el primer binomio.
 en el primer binomio.
en el primer binomio. , igualar la primera expresión binomial a
, igualar la primera expresión binomial a  y perderte
y perderte  sobre. Por lo tanto:
sobre. Por lo tanto:


Entonces, la primera solución del polinomio cuadrático
 es
es  .
.
9. Determinar la segunda solución. haces esto por  para resolver en el segundo binomio.
para resolver en el segundo binomio.
 para resolver en el segundo binomio.
para resolver en el segundo binomio. , igualar la segunda expresión binomial a
, igualar la segunda expresión binomial a  y perderte
y perderte  sobre. Por lo tanto:
sobre. Por lo tanto:


Entonces la segunda solución del polinomio cuadrático es
 igual a
igual a  .
.Consejos
- No se preocupe por las variables, como t, o si tiene una ecuación que equivale a f(x) en lugar de 0. Si la pregunta quiere ver raíces, ceros o factores, trátela como cualquier otro problema.
- Recuerde el orden de las operaciones mientras trabaja: primero borre los paréntesis, luego haga la multiplicación y la división, y finalmente la suma y la resta.
Artículos sobre el tema. "Resuelve polinomios"
Оцените, пожалуйста статью
Popular