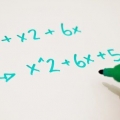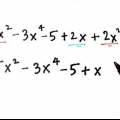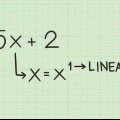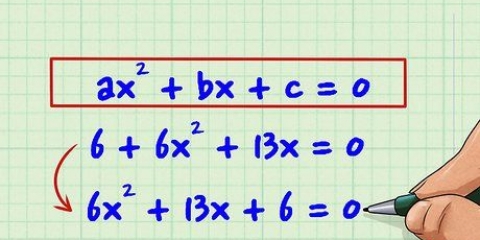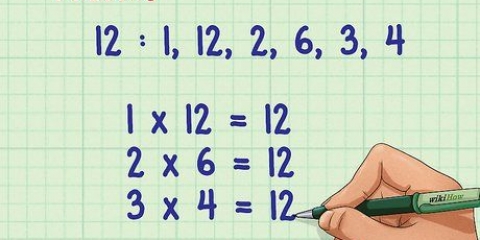Factorizar un polinomio de tercer grado: 12 pasos (con fotos)

Contenido

Pasos
- Parte 1 de 2: disolver por agrupación
- Parte 2 de 2: Factoring con el término libre
Consejos

Este artículo trata sobre la factorización de un polinomio cúbico, también llamado polinomio. Vamos a explorar cómo podemos hacer esto usando agrupación y usando los factores del término libre.

Pasos

Parte 1 de 2: disolver por agrupación

Imagen titulada Factorizar un polinomio cúbico Paso 1

1. Divide el polinomio en dos grupos. Dividir el polinomio ayuda a resolver cada parte individual.

Supongamos que estamos trabajando con el siguiente polinomio:" x + 3x - 6x - 18 = 0. Descompongamos esto en (x + 3x) y (-6x - 18)

Imagen titulada Factorizar un polinomio cúbico Paso 2

2. Trata de averiguar qué es lo mismo en cada grupo.

En (x + 3x), vemos que x es igual.

En (-6x - 18), vemos que -6 es igual.

Imagen titulada Factorizar un polinomio cúbico Paso 3

3. Eliminar estos factores iguales de los dos términos.

Factorizando x obtenemos x(x+3).

Al descomponer -6 de la segunda pieza obtenemos -6(x + 3).

Imagen titulada Factorizar un polinomio cúbico Paso 4

4. Si cada uno de los dos términos contiene el mismo factor, entonces puedes combinar estos factores.

Esto da (x + 3)(x - 6).

Imagen titulada Factorizar un polinomio cúbico Paso 5

5. Encuentre la solución mirando las raíces. Si tienes x en una raíz cuadrada, recuerda que tanto los números positivos como los negativos son válidos para esa ecuación.

Las soluciones son -3 y √6.

Parte 2 de 2: Factoring con el término libre

Imagen titulada Factorizar un polinomio cúbico Paso 6

1. Reordena la expresión de la siguiente forma: hacha+bx+cx+d.

Supongamos que trabajas con la ecuación: x - 4x - 7x + 10 = 0.

Imagen titulada Factorizar un polinomio cúbico Paso 7

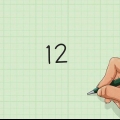
2. Encuentre todos los factores de "D". El constante "D" se convierte en el número sin variables al lado como "X".

Los factores son los números que puedes multiplicar para obtener otro número. En este caso, estos son los factores de 10, o "D": 1, 2, 5 y 10.

Imagen titulada Factorizar un polinomio cúbico Paso 8

3. Encuentre un factor que haga que el polinomio sea igual a cero. Queremos determinar qué factor hace que el polinomio sea igual a cero si aplicamos este factor para "X" completa la ecuacion.

Comience usando el primer factor, 1. sustituir "1" para cada "X" en la comparación:
(1) - 4(1) - 7(1) + 10 = 0

Esto da: 1 - 4 - 7 + 10 = 0.

Como 0 = 0 es un enunciado verdadero, sabes que x = 1 es la solución.

Imagen titulada Factorizar un polinomio cúbico Paso 9

4. Ahora ve a reorganizar todo. Si x=1 entonces es posible escribir esta ecuación ligeramente diferente sin cambiar el significado.

"X = 1" es lo mismo que "x - 1 = 0" o "(x - 1)". solo tienes uno "1" restado de cada lado de la ecuación.

Imagen titulada Factorizar un polinomio cúbico Paso 10

5. Factorizar la raíz cuadrada de la ecuación. "(x - 1)" es la raiz. Trate de factorizar estos fuera del resto de la ecuación. Haz esto con un polinomio a la vez.

¿Puedes factorizar (x - 1) de x?? No, eso no es posible. Pero si primero tomas prestada una -x de la segunda variable: x(x - 1) = x - x.

¿Puedes factorizar (x - 1) a partir de lo que queda de la segunda variable?? No, esto tampoco es posible aquí. Tienes que pedir prestado algo de la tercera variable nuevamente, que es 3x de -7x. Esto nos da -3x(x - 1) = -3x + 3x.

Como sacaste 3x de -7x, la tercera variable ahora es -10x y la constante es 10. ¿Puedes desvincular esto?. Sí, por supuesto! -10(x - 1) = -10x + 10.

Lo que has hecho es reorganizar las variables para que puedas obtener el factor (x - 1) de toda la ecuación. La ecuación modificada se ve así: x - x - 3x + 3x - 10x + 10 = 0, pero sigue siendo la misma que x - 4x - 7x + 10 = 0.

Imagen titulada Factorizar un polinomio cúbico Paso 11

6. Proceder a reemplazar los factores del término libre. Mira los números que resolviste usando (x - 1) en el Paso 5:

x(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Puede reorganizarlos para que sea más fácil disolverlos nuevamente: (x - 1)(x - 3x - 10) = 0.

Aquí solo estás tratando de factorizar (x - 3x - 10). Los factores entonces se convierten en (x + 2)(x - 5).

Imagen titulada Factorizar un polinomio cúbico Paso 12

7. Tu solución son las raíces factorizadas. Verifique esta solución insertando cada uno de ellos nuevamente en la ecuación original.

(x - 1)(x + 2)(x - 5) = 0 Esto da las soluciones para 1, -2 y 5.

Inserta -2 en la ecuación: (-2) - 4(-2) - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0.

Inserta 5 en la ecuación: (5) - 4(5) - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.

Consejos

La ecuación cúbica es el producto de 3 ecuaciones de primer grado o de una ecuación de primer grado y una ecuación de segundo grado que no se puede factorizar. En el último caso, después de encontrar el polinomio de primer grado, usa la división larga para encontrar el polinomio de segundo grado.
No hay polinomios cúbicos que no se puedan factorizar cuando se trata de números reales, porque esta ecuación debe tener una raíz cuadrada de números reales. Las ecuaciones de tercer grado como x + x + 1 que tienen una raíz real irracional no se pueden factorizar en polinomios con números enteros o racionales como coeficiente. Aunque se puede factorizar en la ecuación misma, no se puede reducir a un polinomio entero.

El método 2 equivale a la división larga de dos polinomios, un.v:

(x-1) ∕x³ - 4x²-7x+10 ∕

- 10x + 10................= (x-1) (-10)

Los determinantes x², -3x y -10 del cociente se obtienen restando siempre el 1er término del divisor ( x ) al primer término del dividendo, o lo que queda de él ( x³, -3x², -10x ).