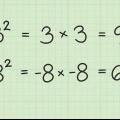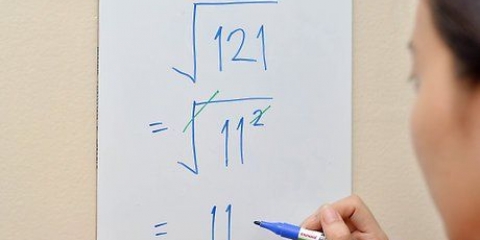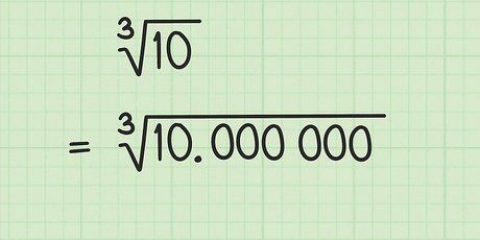Simplificar raíces cuadradas

Contenido

Pasos
Consejos
Advertencias

Simplificar una raíz cuadrada no es tan difícil como parece. Para simplificar una raíz cuadrada, solo necesita factorizar el número de la raíz cuadrada e intentar sacar la raíz cuadrada de uno o ambos factores. Una vez que conozcas algunos números cuadrados comunes y sepas cómo dividir un número en factores, estarás bien encaminado para simplificar una raíz cuadrada. Así es como puedes aprender esto rápidamente.

Pasos

Método 1 de 4: simplificar la raíz cuadrada de un número

Imagen titulada Simplifica una raíz cuadrada Paso 1

1. Aprende algunos números cuadrados y sus raíces. Elevar al cuadrado, multiplicar un número por sí mismo, hace un número al cuadrado (perfectamente cuadrado). Por ejemplo: 25 es un número al cuadrado porque 5 x 5, o 5, es igual a 25. Saber al menos los primeros 10 diez números al cuadrado puede ayudar a reconocer y simplificar las raíces cuadradas. Aquí están los primeros diez números al cuadrado:

1 = 1
2 = 4
3 = 9
4 = 16
5 = 25
6 = 36
7 = 49
8 = 64
9 = 81
10 = 100

2. Encontrar la raíz cuadrada de un número cuadrado. Si ve un número cuadrado debajo de un radical, entonces solo necesita eliminar el radical (√) y escribir la raíz cuadrada del número cuadrado. Si ya te habías aprendido esto de memoria, entonces ya terminaste. Si el número es demasiado grande y no está seguro de si es un número cuadrado, intente encontrar la raíz cuadrada con su calculadora para verificar si produce un buen número redondo. Por ejemplo: en √25 sabes que la respuesta es igual a 5 porque 25 es un número al cuadrado.

Método 2 de 4: simplificar una raíz cuadrada mediante la factorización

Imagen titulada Simplifica una raíz cuadrada Paso 4

1. Si el número es par, se divide por 2. Encontrar los factores de un número implica encontrar todos los números que multiplicados entre sí producen ese número, lo que facilita determinar su raíz cuadrada. Si es un número par entonces lo primero que puedes hacer es dividir el número por 2. En este ejemplo puedes dividir √98 en √(2x49), porque 98 : 2 =49. Si el número no es divisible por 2, prueba con 3, 4, 5, y así sucesivamente, hasta que encuentres la combinación correcta.

Imagen titulada Simplifica una raíz cuadrada Paso 5

2. Divide estos factores nuevamente en factores para encontrar más números cuadrados. A ver si puedes seguir dividiendo el número en factores. 2 es primo y solo se tiene a si mismo y 1 como divisor. Pero 49, el otro factor, todavía se puede dividir en 7 x 7, porque es un número cuadrado. Entonces puedes reescribir la raíz √(2x49) como √(2x7x7), o √[2(7)], lo que significa que ya hemos encontrado el número cuadrado que buscábamos.

Imagen titulada Simplifica una raíz cuadrada Paso 6

3. Simplifica la raíz cuadrada. Como √98= √[2(7)], es posible colocar un 7 fuera del radical y simplificar la respuesta a 7√2. Entonces √49 o también (7 x 7), luego se convierte en 7 tan pronto como lo colocas fuera del radical. Si vuelves a colocar el 7, vuelve a ser un número cuadrado y por lo tanto 49. Entonces, √98 = 7√2.

Método 3 de 4: otros métodos para simplificar una raíz cuadrada

1. Si no logra encontrar un número cuadrado de inmediato, divida el número aún más. Por ejemplo, si el problema es √48, continúas dividiendo hasta que no puedes ir más allá de 2x2, de modo que 4 se convierte en un coeficiente del radical y 3 permanece dentro del radical. Así es como funciona:

√48 = √(2x24)
√(2x24) = √(2x12x2)
√(2x12x2) = √(2x6x2x2)
√(2x6x2x2) = √(2x3x2x2x2)
√(2x3x2x2x2) = √(2x3)
√(2x3)= 4√3
√48 = 4√3

2. Recuerda que no puedes simplificar un número primo. Eso es porque los factores aquí son 1 y el número primo en sí. Por ejemplo: √17 no se puede simplificar porque 17 es primo.

3. Dividir en factores de más de un número al cuadrado. Si los factores del número contienen más de un número cuadrado, sáquelos todos fuera del radical. Si ha encontrado varios cuadrados mientras simplificaba, sáquelos todos fuera del radical y multiplíquelos. Por ejemplo: supongamos que desea simplificar el número √32, luego divídalo en los factores 4 x 4 x 2, teniendo en cuenta que el número cuadrado 4 aparece dos veces. Haz este 16√2 que eventualmente producirá 4√2.

4. No confundas el coeficiente con una raíz de potencia más alta. 3√125, por ejemplo, es igual a 3 x √125, pero √125 es la raíz cúbica de 125. (porque 5 x 5 x 5 = 125, √125 = 5.)

Método 4 de 4: conocer la terminología

1. Recuerda que el radical (√) es el símbolo de la raíz cuadrada. Por ejemplo, en el problema √25, "√" el signo radical.

2. Recuerda que el radical es el número debajo del radical. Encuentra la raíz cuadrada de este número. Por ejemplo: en √25 es "25" el numero raiz.

3. Recuerda que el coeficiente es el número fuera del radical. Este número multiplica la raíz cuadrada; Esto se puede encontrar a la izquierda del signo radical, el símbolo √. Por ejemplo: en 7√2, "7" el coeficiente.

4. Recuerda que un factor es un número que cabe completamente en otro número. Por ejemplo: 2 es un factor de 8 porque 8 ÷ 4 = 2, pero 3 no es un factor de 8 porque 8 ÷ 3 no responde a un número entero. Por ejemplo: 5 es factor de 25 porque 5 x 5 = 25.

5. Comprender el significado de simplificar una raíz cuadrada. Simplificar una raíz cuadrada simplemente implica dividir un cuadrado de una raíz cuadrada en factores, luego moverlo a la izquierda del radical, dejando el otro factor dentro del radical. Si el número es un número cuadrado, puede eliminar el signo radical tan pronto como haya escrito su raíz cuadrada. Por ejemplo: √98 se puede simplificar a 7√2.

Consejos

Una forma de encontrar cuadrados para dividir sus números al cuadrado es buscar cuadrados en su lista comenzando con el número más pequeño después de su número al cuadrado. Por ejemplo: si está buscando el número cuadrado de 27, comience en 25 y deténgase en 9, porque ha encontrado el mayor divisor que es un número cuadrado.

Advertencias

No use calculadoras, excepto en el paso en el que está tratando de averiguar cuántas veces el cuadrado entra en la raíz cuadrada.
No es lo mismo simplificar que poner valores en una ecuación.En ninguna parte de todo el proceso puede aparecer un número decimal en ninguna parte!