Ejemplo: la siguiente expresión 2x + 4(5 + 2) + 3 - (3 + 4/2). Primero resuelve los términos entre paréntesis, entonces 5 + 2 y 3 + 4/2. 5 + 2 = 7. 3 + 4/2 = 3 + 2 = 5. El término entre el segundo par de corchetes se convierte en 5 porque primero tenemos que calcular 4/2 y luego resolver la suma. Si simplemente trabajáramos de izquierda a derecha, entonces la suma sería 3 + 4: 2, por lo que primero se calcularía 3 + 4 y luego 7 / 2, lo que daría como resultado la respuesta incorrecta 7/2. Nota: si hay varios paréntesis anidados (paréntesis dentro de paréntesis), disuelva primero el más interno y trabaje hacia los paréntesis más externos. 
Después de resolver los paréntesis, el ejemplo quedó así. 2x + 4(7) + 3 - 5. La única potencia en nuestro ejemplo es 3, y esto es igual a 9. La expresión ahora se convierte en 2x + 4(7) + 9 - 5. 
Hay dos multiplicaciones en el problema: 2x (2x es 2 × x) y 4(7). No sabemos el valor de x, así que dejémoslo como 2x. 4(7) = 4 × 7 = 28. Podemos escribir esto de manera diferente como 2x + 28 + 9 - 5. 
Como ya resolvimos un problema de división que estaba entre paréntesis, no quedan problemas de división en nuestro problema, por lo que podemos omitir este paso. Esto plantea un punto importante: si una operación no ocurre en una expresión, continúe con la siguiente operación como se indica en las reglas de reglas matemáticas. 
Nuestra expresión ahora está parcialmente simplificada a "2x + 28 + 9 - 5". Ahora sumamos tanto como sea posible, de izquierda a derecha. No podemos sumar 2x a los otros números, porque no sabemos el valor de x, así que nos saltamos este. 28 + 9 = 37, entonces podemos reescribir la expresión como "2x + 37 - 5". 
En nuestra expresión, "2x + 37 - 5", solo hay una resta,37 - 5 = 32 
Nuestra respuesta final es "2x + 32". No podemos resolver la suma sin saber el valor de x, pero una vez que lo sabemos, es mucho más fácil de resolver que la expresión original. 

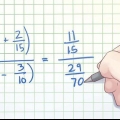
Por ejemplo, supongamos que tenemos que resolver la fracción 36/60. Si tenemos una calculadora a mano, la respuesta (6) se calcula así. Si no tenemos esto, podemos recorrer un largo camino eliminando factores similares. Otra forma de pensar en 36/60 es como (6 × 6)/(6 × 10). Esto se puede volver a escribir como 6/6 × 6/10. 6/6 = 1, por lo que nuestra expresión se convierte en 1 × 6/10 = 6/10. Pero aún no hemos llegado allí: tanto 6 como 10 tienen el mismo factor de 2. Repitiendo el procedimiento anterior, mantenemos3/5 acerca de. 
Supongamos que tenemos la expresión (3x + 3x)/(-3x + 15x).Esta fracción se puede reescribir como (x + 1)(3x)/(3x)(5 - x), 3x aparece tanto en el numerador como en el denominador. Eliminando estos factores de la ecuación se obtiene (x + 1)/(5 - x). Asimismo, este es el caso de la ecuación (2x + 4x + 6)/2. Como todo término es divisible por 2, podemos reescribirlo como (2(x + 2x + 3))/2 y así simplificar a x + 2x + 3. Eso sí, no puedes eliminar todos los términos, solo aquellos factores que están tanto en el numerador como en el denominador. Por ejemplo, la expresión (x(x + 2))/x, donde el "X" se puede quitar de la fracción, dejando (x + 2)/1 = (x + 2). Pero (x + 2)/x no es para simplificar a 2/1 = 2. 
Por ejemplo, la expresión 3(x + 8 se puede simplificar a3x + 24, mientras que 3x(x + 8) se puede simplificar a 3x + 24x. Tenga en cuenta que en algunos casos, como con fracciones variables, la constante fuera de los paréntesis se puede usar en la simplificación y, por lo tanto, no se debe multiplicar. Por ejemplo, en la fracción (3(x + 8))/3x, el factor 3 ocurre tanto en el numerador como en el denominador, por lo que podemos cancelarlo y simplificar la expresión a (x + 8)/x. Esto es más simple y fácil de trabajar que con (3x + 24x)/3x, que habría sido la respuesta si hubiéramos multiplicado. 
Echa otro vistazo a la expresión x - 5x + 6. Esto se puede resolver en (x - 3)(x - 2). Entonces, si x - 5x + 6 es el numerador de una ecuación con uno de estos factores en el denominador (como en (x - 5x + 6)/(2(x - 2))), entonces podemos factorizarlo en factores tales que podemos deshacernos del denominador. En otras palabras, en (x - 3)(x - 2)/(2(x - 2)), (x - 2) desaparece, dejándonos(x - 3)/2 sobrante. Como se indicó anteriormente, también puede resolver una ecuación con factorización, especialmente si se establece igual a cero. Por ejemplo: toma la ecuación x - 5x + 6 = 0. La factorización nos da (x - 3)(x - 2) = 0. Como un número multiplicado por cero es igual a cero, podemos igualar ambos términos a cero para encontrar la respuesta a este problema. Entonces la respuesta a la ecuación es x=3 y x= 2.
Simplificar expresiones matemáticas
Contenido
Los problemas de matemáticas a menudo piden una respuesta "lo más sencillo posible" escribir, en otras palabras, dar una respuesta lo más elegante posible. Si bien una expresión larga y torpe y una versión más corta y elegante técnicamente significan lo mismo, a menudo no se acepta una respuesta hasta que se haya simplificado tanto como sea posible.Además, las respuestas simplificadas también son más fáciles de trabajar. `Es por eso que aprender a simplificar es una habilidad esencial para los futuros matemáticos.
Pasos
Método 1 de 2: el orden de las operaciones matemáticas

1. El orden de las operaciones. Al simplificar expresiones matemáticas, no puede simplemente evaluar de izquierda a derecha. Ciertas operaciones tienen prioridad sobre otras y, por lo tanto, deben realizarse primero. Si no hace esto, puede obtener la respuesta incorrecta. El orden de las operaciones en matemáticas es el siguiente: Paréntesis, Exponenciación y Raíz, Multiplicación y División, Suma y Resta. Un mnemotécnico para recordar esta secuencia es "¿Cómo debemos deshacernos de lo inadecuado? " o "HMWVDOA".
- Tenga en cuenta que si bien un conocimiento básico de las operaciones es suficiente para resolver la mayoría de las expresiones estándar, se necesitan técnicas especiales para resolver expresiones que contienen variables, incluida la mayoría de los polinomios. Mire el Método dos para obtener más información.

2. Comienza resolviendo todos los términos entre paréntesis. En matemáticas, los paréntesis significan que todos los términos que encierran deben resolverse por separado de la expresión circundante. Independientemente de las operaciones, asegúrese de resolver todos los términos entre paréntesis primero si desea simplificar una expresión. Tenga en cuenta que las reglas de cálculo para el orden de las operaciones también se aplican entre paréntesis. Entonces aquí también primero paréntesis, luego exponenciación, etc.

3. Ahora disuelva los poderes. Después de resolver los paréntesis, ahora puede pasar a la exponenciación. Resuélvelos uno por uno.

4. Ahora resuelve las sumas de multiplicación. Recuerda que una multiplicación se puede escribir de varias formas. Con un punto, sin un punto o con un símbolo ×. Pero también algo como 4(x)) indica una multiplicación.

5. Continuar con los problemas de división. Si estás buscando problemas de división, recuerda que estos también se pueden escribir de diferentes maneras. El símbolo ÷ simple, con dos puntos o una barra oblicua (como 3/4) todos indican una división.

6. Agregar. Ahora suma los diferentes términos. Resuelva esto de izquierda a derecha, como está en la expresión y lo que sea más conveniente. Por ejemplo, en la suma 49 + 29 + 51 +71, es más fácil dividir el problema en los siguientes bloques: 49 + 51 = 100, 29 + 71 = 100 y 100 + 100 = 200. Esto es más fácil que 49 + 29 = 78, 78 + 51 = 129 y 129 + 71 = 200.

7. sustraer. El último paso de las operaciones es restar los términos restantes. Calcule el resto de su expresión, de izquierda a derecha. Puede hacer la suma de números negativos en este paso o en el anterior; no importa para su respuesta.

8. Ver tu expresión. Después de trabajar con la secuencia de operaciones, te quedan varios términos en la forma más simplificada. Si hay una o más variables en la expresión, permanecen prácticamente sin cambios. Simplificar expresiones con variables requiere que resolvamos más estas ecuaciones para las incógnitas, o que usemos métodos especiales (vea el siguiente paso).
Método 2 de 2: simplificar expresiones complejas

1. Sumar potencias variables iguales. Cuando se trata de expresiones que contienen variables, es importante recordar que los términos con la misma variable y el mismo exponente (o "términos iguales") se pueden sumar (o restar) como números regulares. Los términos deber no solo tienen la misma variable, sino también el mismo exponente. Por ejemplo, 7x y 5x se pueden sumar, pero 7x y 5x no.
- Esta regla también se puede extender a términos multivariados. Por ejemplo, 2xy se puede agregar a -3xy, pero no -3xy o -3y.
- Toma las siguientes expresiones:x + 3x + 6 - 8x. En esta expresión, podemos sumar los términos 3x y -8x porque son iguales entre sí. Nuestra expresión entonces se simplifica: x - 5x + 6.

2. Simplificar fracciones eliminando o dividiendo factores. Las fracciones que consisten solo en números (y sin variables) se pueden simplificar de varias maneras. Una fracción es solo una suma de división y debe tratarse como tal. Además, si se da la misma multiplicación en el numerador o en el denominador, se puede eliminar, porque ya dan respuesta 1 al compartir. En otras palabras, si el numerador y el denominador tienen el mismo factor, entonces se puede eliminar de la fracción, simplificando el resultado.

3. Si está tratando con fracciones que contienen variables, intente eliminar las variables. Estas expresiones ofrecen posibilidades únicas para simplificar. Al igual que las fracciones regulares, las fracciones variables te permiten eliminar factores que están tanto en el numerador como en el denominador. Pero en el último caso, estos factores pueden ser tanto números como variables.

4. Multiplica los términos entre paréntesis por sus constantes. Cuando se trata de términos variables entre paréntesis más una constante, multiplicar cualquier término dentro de los paréntesis por la constante fuera de los paréntesis puede resultar en una expresión más simple.Esto se aplica tanto a las constantes numéricas como a las constantes con variables.

5. simplificar factorizando. Esta es una técnica que puede simplificar algunas ecuaciones. Al factorizar, piense en algo que sea lo opuesto a "paréntesis de multiplicación" – a veces una ecuación se puede representar más simplemente como dos términos multiplicados juntos que como una sola ecuación. Esto es especialmente cierto si puede eliminar parte de la ecuación con él. En ciertos casos (como con ecuaciones cuadráticas) también puede resolver la ecuación en sí misma con factorización.
Artículos sobre el tema. "Simplificar expresiones matemáticas"
Оцените, пожалуйста статью
Popular