Formular pruebas matemáticas

Contenido

Pasos
Consejos

Las demostraciones matemáticas pueden ser difíciles, pero con el conocimiento previo adecuado tanto de las matemáticas como de la estructura de una demostración, ciertamente puede formularlas con éxito. Desafortunadamente, no existe una manera rápida y fácil de aprender a crear pruebas. Necesita una base sólida en su conocimiento de la materia para llegar a los teoremas y definiciones correctos para desarrollar su prueba lógicamente. Al leer ejemplos y practicar usted mismo, podrá dominar la habilidad de las pruebas matemáticas.

Pasos

Método 1 de 3: comprender el problema

1. entender la pregunta. Primero debe determinar exactamente qué es lo que está tratando de probar. Esta pregunta también servirá como el teorema final de la prueba. En este paso, también definirá las suposiciones con las que trabajará. Identificar la pregunta y hacer las suposiciones necesarias le brinda un punto de partida para comprender el problema y resolver la evidencia.

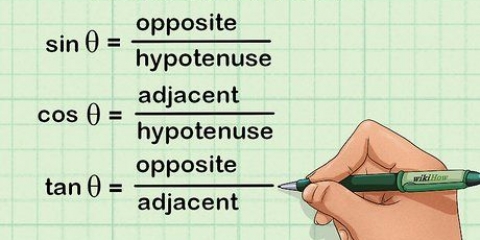
2. dibujar diagramas. Al tratar de comprender el funcionamiento interno de un problema matemático, a veces es más fácil dibujar un diagrama de lo que está sucediendo. Los diagramas son particularmente importantes en las pruebas geométricas porque te permiten visualizar lo que realmente quieres probar.

Usa la información dada en el problema para hacer un dibujo de la prueba. Nombrar a los conocidos y extraños.

Al elaborar la evidencia, utilice la información necesaria para sustentar la evidencia.

Imagen titulada Haz Pruebas Matemáticas Paso 3

3. Estudiar demostraciones de teoremas relacionados. Las pruebas son difíciles de aprender a componer, pero una excelente manera de aprender esto es estudiar los teoremas relacionados y cómo se demostraron.

¿Te das cuenta de que una prueba es solo un buen argumento donde se fundamenta cada paso?. Puede encontrar mucha evidencia para estudiar tanto en línea como en un libro de texto.

4. Hacer preguntas. Es muy normal quedarse atascado en la evidencia. Pregúntale a tu maestro o compañeros de clase si no puedes resolverlo. Este último puede tener preguntas similares y pueden trabajar juntos en los problemas. Es mejor hacer preguntas y luego comprender que vadear ciegamente la evidencia.

Consulte con su maestro después de la clase para obtener una explicación adicional.

Método 2 de 3: estructurar una prueba

1. Definir demostraciones matemáticas. Una prueba matemática es una serie de enunciados lógicos respaldados por teoremas y definiciones, que prueban la exactitud de otro enunciado matemático. Las demostraciones son la única forma de saber si una afirmación es matemáticamente válida.

Ser capaz de formular una prueba matemática indica una comprensión fundamental del problema en sí y de todos los conceptos involucrados en el problema.
La evidencia también te obliga a mirar las matemáticas de una manera nueva y emocionante. Con solo tratar de probar algo, obtiene más conocimiento y comprensión al respecto, incluso si su evidencia finalmente no parece correcta.

2. Conoce a tu audiencia. Antes de escribir una prueba, debe pensar en la audiencia para la que la está escribiendo y en lo que ya saben. Si escribe una prueba para una publicación, lo hará de manera diferente que para una clase de secundaria.

Conocer a su audiencia lo ayudará a articular la evidencia de una manera que comprenderá dada la cantidad de conocimientos previos que tiene la audiencia.

Imagen titulada Haz Pruebas Matemáticas Paso 7

3. Comprender el tipo de evidencia que está formulando. Hay algunos tipos diferentes de pruebas, y la que elija dependerá de su público objetivo y de la tarea. Si no está seguro de qué versión usar, pídale consejo a su maestro. En la escuela secundaria, es posible que debas formular la prueba en un formato específico, como una prueba formal de dos columnas.

Una prueba de dos columnas es una estructura en la que los datos y las afirmaciones se colocan en una columna y la evidencia de apoyo al lado en una segunda columna. Son muy utilizados en geometría.

Una prueba informal en párrafos usa declaraciones gramaticalmente correctas y menos símbolos. En un nivel superior, siempre debe usar una prueba informal.

4. Escriba la prueba en dos columnas como una descripción general. Estructurar una prueba en dos columnas es una manera fácil de organizar sus pensamientos y considerar el problema. Dibuje una línea en el centro de la página y escriba todos los datos y declaraciones a la izquierda. Escriba las definiciones/afirmaciones correspondientes a la derecha, junto a los datos que respaldan.

Por ejemplo:

El ángulo A y el ángulo B forman un par lineal. Dato.

El ángulo ABC es recto. Definición de ángulo recto.

el angulo abc mide 180°. Definición de una línea.

Ángulo A + ángulo B = ángulo ABC. Postulado para sumar ángulos.

Ángulo A + ángulo B = 180°. sustitución.

Ángulo A como complemento del ángulo B. Definición de ángulos adicionales.

q.mi.D.

5. Convierta la prueba en dos columnas en una prueba informal. A partir de la prueba en dos columnas, escriba una prueba informal como un párrafo sin demasiados símbolos y abreviaturas.

Por ejemplo: supongamos que los ángulos A y B son pares lineales. La hipótesis es que el ángulo A y el ángulo B se complementan (son suplementarios). El ángulo A y el ángulo B forman una línea recta porque son pares lineales. Una recta se define como la que tiene un ángulo de 180°. Dado el postulado de la suma de ángulos, los ángulos A y B juntos forman la línea ABC. Por sustitución, A y B juntos suman 180°, por lo tanto son ángulos suplementarios. q.mi.D.

Método 3 de 3: Formulación de la evidencia

1. Aprende el vocabulario de la prueba matemática. Hay ciertas declaraciones y oraciones que ves una y otra vez en una demostración matemática. Estas son las oraciones con las que debe estar familiarizado y poder usar al formular su propia evidencia.

`Si A, entonces B` significa que tienes que demostrar que si A es verdadero, B también debe ser verdadero.
`A si y solo si B` significa que tienes que probar que A y B son verdaderos y falsos al mismo tiempo. Demuestre tanto `Si A, entonces B` como `Si no A, entonces no B`.
`A solo si B` significa lo mismo que `Si A, entonces B`, por lo que no se usa con frecuencia. Es bueno ser consciente de esto cuando te lo encuentras.
Al preparar la evidencia, evite usar "yo" en favor de "nosotros".

2. Registrar todos los datos. Al compilar una prueba, el primer paso es identificar y registrar todos los datos. Este es el mejor lugar para comenzar, ya que lo ayudará a pensar sobre lo que se sabe y qué información necesita para completar la prueba. Lee el problema y escribe cada detalle.

Por ejemplo: Demostrar que dos ángulos que forman un par lineal (ángulo A y ángulo B) son suplementarios.

Dado: el ángulo A y el ángulo B forman un par lineal

Prueba: el ángulo A es suplementario al ángulo B.

3. Definir todas las variables. Además de escribir los datos, es útil definir todas las variables. Escriba las definiciones al principio de la demostración para evitar confusiones al lector. Si las variables no están definidas, un lector podría perderse fácilmente al tratar de comprender su evidencia.

No use variables en su prueba que aún no estén definidas.

Por ejemplo: Las variables son las medidas del ángulo A y el ángulo B.

4. Trabajar a través de la evidencia al revés. A menudo es más fácil pensar al revés sobre un problema. Comience con la conclusión, lo que está tratando de probar, y piense en los pasos que pueden llevarlo de regreso al principio.

Edite los pasos al principio y al final para ver si son similares. Use los datos, las definiciones que ha aprendido y evidencia similar.

Hágase preguntas en el camino. `Por qué esto es tan?` y `¿Hay alguna manera de que esto no sea cierto??son buenas preguntas para cualquier reclamo o reclamación.

No olvides escribir los pasos en el orden correcto para la prueba final.

Por ejemplo: si los ángulos A y B son suplementarios, entonces deben formar 180° juntos. Los dos ángulos juntos forman la línea ABC. Sabes que forman una línea debido a la definición de pares lineales. Como una línea recta mide 180°, puedes usar la sustitución para probar que el ángulo A y el ángulo B suman 180°.

5. Coloca tus pasos en orden lógico. Comience la prueba desde el principio y trabaje hasta llegar a la conclusión. Si bien es útil pensar en la evidencia, al comenzar con la conclusión y trabajar hacia atrás, presentar la evidencia real pondrá la conclusión al final. Las afirmaciones en la evidencia deben seguir una de la otra, con justificación para cada afirmación, de modo que no haya razón para dudar de la validez de su evidencia.

Comience indicando las suposiciones con las que está trabajando.

Divídalos en pasos simples y directos para que el lector no tenga que preguntarse cómo se sigue lógicamente un paso de otro.

No es raro formular múltiples pruebas. Siga reorganizando hasta que todos los pasos estén en el orden más lógico.

Por ejemplo: empezar por el principio.

El ángulo A y el ángulo B forman un par lineal.

El ángulo ABC es recto.

el angulo abc mide 180°.

Ángulo A + ángulo B = ángulo ABC.

Ángulo A + ángulo B = 180°.

El ángulo A es suplementario al ángulo B.

6. Evitar el uso de flechas y abreviaturas en las pruebas escritas. Cuando delinea el plan para su prueba, puede usar taquigrafía y símbolos, pero al escribir la prueba final, los símbolos, como las flechas, pueden confundir al lector. Use palabras como "entonces" o "entonces" en su lugar.

Las excepciones al uso de abreviaturas son: p. (por ejemplo) y d.w.z. (eso es), pero asegúrese de usarlos correctamente.

7. Apoye todas las declaraciones con un teorema, ley o definición. Una prueba es tan buena como la prueba utilizada. No se puede hacer una afirmación sin fundamentarla con una definición. Referirse a otra evidencia similar como ejemplo.

Tratar de aplicar su evidencia a un caso en el que falso debería ser, y comprobar si este es realmente el caso. Si el resultado no es falso, modifique la prueba para que sea.

Muchas pruebas geométricas se escriben como una prueba de dos columnas, con el enunciado y la prueba. Una prueba matemática formal destinada a la publicación se escribe como gramática correcta de párrafo.

8. Termine con una conclusión o Q.mi.D. La última declaración de la prueba debe ser la hipótesis que estaba tratando de probar. Una vez que haya hecho esta declaración, cierre la prueba con un símbolo final, como Q.mi.D. o un cuadrado cerrado, para indicar que la demostración está completa.

q.mi.D. significa `quod erat demostrandum` (en latín, `lo que tenía que ser probado`).

Si no está seguro de si su prueba es correcta, simplemente escriba en unas pocas oraciones cuál es su conclusión y por qué es importante.