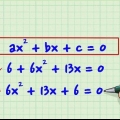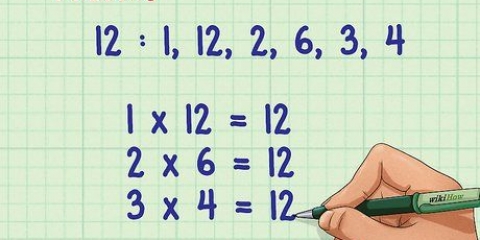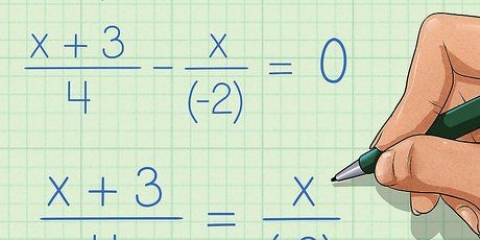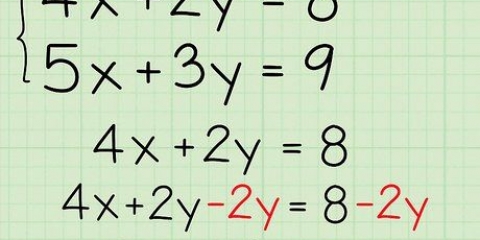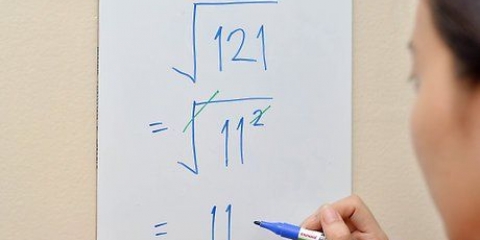Por ejemplo: si quieres dividir 20 en factores, puedes escribirlo como 4×5. Tenga en cuenta que los términos variables también se pueden escribir como factores. - Por ejemplo, 20x se puede escribir como 4(5x). Los números primos no se pueden escribir como factores porque solo son divisibles por ellos mismos y 1. 
ehmurciélagos metrosubir ocho Wcontracción nerviosa Vmultiplicar Dellen Ocontar asustraer 

Por ejemplo, encontremos los términos semejantes en nuestra ecuación 1 + 2x - 3 + 4x. 2x y 4x tienen la misma variable elevada a la misma potencia (en este caso, las variables x no tienen ningún exponente). Además, 1 y -3 son términos iguales, porque ninguno tiene una variable. Entonces en esta ecuación están 2x y 4x y 1 y 3 términos iguales. 
Sumamos los términos semejantes en nuestro ejemplo. 2x + 4x = 6x 1 + -3 = -2 
En nuestro ejemplo, los términos simplificados eran 6x y -2, por lo que la nueva expresión se convierte en 6x - 2. Esta expresión simplificada es equivalente a la original (1 + 2x - 3 + 4x), pero es más corta y fácil de calcular con. Es más fácil factorizar, lo que, como veremos a continuación, es una habilidad importante para poder simplificar. 
Por ejemplo, supongamos que tenemos la ecuación 5(3x-1) + x((2x)/(2)) + 8 - 3x. Entonces sería incorrecto considerar inmediatamente 3x y 2x como términos iguales y combinarlos, porque los paréntesis en la expresión dictan que tenemos que hacer otras operaciones primero. Primero, realicemos las operaciones aritméticas en la expresión según el orden de las operaciones, para obtener los términos que tenemos bien puedo usar. Vea abajo: 5(3x-1) + x((2x)/(2)) + 8 - 3x 15x - 5 + x(x) + 8 - 3x 15x - 5 + x + 8 - 3x. aprobar ahora ya que las únicas operaciones que quedan son la suma y la resta, ¿podemos combinar los términos semejantes?. x + (15x - 3x) + (8 - 5) x + 12x + 3 

Factoricemos nuestra ecuación usando el máximo común divisor, 3. Hacemos esto dividiendo cada término por 3. 9x/3 = 3x 27x/3 = 9x -3/3 = -1 Entonces la nueva expresión es 3x + 9x - 1. 
Para nuestra expresión de ejemplo, 3x + 9x - 1, ponemos la expresión entre paréntesis y multiplicamos este término por el máximo común divisor de la ecuación original para convertir 3(3x + 9x - 1) Llegar. Esta ecuación es equivalente a la original, 9x + 27x - 3. 
Supongamos que nuestra expresión de ejemplo original, 9x + 27x - 3, es igual al numerador de una fracción más grande con 3 como denominador. Esta fracción se ve así: (9x + 27x - 3)/3. Podemos usar la factorización para simplificar esta fracción. Agregue la forma factorizada de nuestra expresión original al numerador: (3(3x + 9x - 1))/3 Tenga en cuenta que tanto el numerador como el denominador tienen 3 como coeficiente. Si divides el numerador y el denominador por 3, obtienes: (3x + 9x - 1)/1. Porque una fracción con "1" en el denominador es igual a los términos en el numerador, podemos decir que nuestra fracción original se puede simplificar a 3x + 9x - 1. 

Tomemos un ejemplo simple - √(90). Si tomamos el número 90 como producto de los dos factores, 9 y 10, podemos calcular la raíz cuadrada de 9 para obtener 3, y ponerlo delante del radical. En otras palabras: (90) √(9×10) (√(9) × √(10)) 3 × √(10) 3√(10) 
Por ejemplo, supongamos que tenemos la expresión 6x × 8x + (x/x). En cualquier caso donde sea necesario multiplicar o dividir exponentes, restamos o sumamos los exponentes respectivamente, para resolver rápidamente un término simplificado. Vea abajo: 6x × 8x + (x/x) (6×8)x + (x) 48x + x Para obtener una explicación, consulte a continuación: Multiplicar términos exponenciales es esencialmente lo mismo que multiplicar series largas de términos sin exponentes. Por ejemplo, porque x = x × x × x y x= x × x × x × x × x, x × x = (x × x × x) × (x × x × x × x × x), o x. Asimismo, dividir términos exponenciales es lo mismo que dividir largas secuencias de términos sin exponentes. x/x = (x × x × x × x × x)/(x × x × x). Como cualquier término en el numerador se puede cancelar contra el mismo término en el denominador, nos quedamos con dos veces una x en el numerador y ninguna en el denominador, dejándonos con x como respuesta.
Simplificar ecuaciones matemáticas
Contenido
Ser capaz de simplificar ecuaciones algebraicas es una parte esencial para dominar los conceptos básicos del álgebra y una herramienta extremadamente valiosa para todos los matemáticos. La simplificación le permite a un matemático cambiar una expresión compleja, larga y/o torpe a una forma más simple o más conveniente pero equivalente. Los conceptos básicos de la simplificación son bastante fáciles de aprender, incluso para alguien que odia las matemáticas. Siguiendo unos sencillos pasos es posible simplificar muchas de las expresiones algebraicas más comunes sin ningún conocimiento matemático especial.
Pasos
Método 1 de 4: comprender los conceptos clave

1. Determinar "términos iguales" según sus variables y potencias. Poseer en álgebra "términos iguales" sobre las mismas variables, elevadas a la misma potencia. En otras palabras, dos términos son "similar", cuando tienen la(s) misma(s) variable(s), o ninguna, y cuando cada variable tiene la misma potencia, o ninguna. El orden de las variables dentro de un término no importa.
- Por ejemplo, 3x y 4x son términos iguales porque cada término tiene una variable x elevada a la segunda potencia. La variable x y x no son términos iguales, porque x tiene una potencia diferente en cada término. Asimismo, -3yx y 5xz no son términos iguales, porque cada término se compone de diferentes variables.

2. Factorizar escribiendo los números como el producto de dos factores. La factorización es una forma de escribir un número dado como el producto de dos factores. Los números pueden estar formados por múltiples factores, por ejemplo, el número 12, que puede estar formado por 1 × 12, 2 × 6 y 3 × 4, por lo que podemos decir que 1, 2, 3, 4, 6, y 12 son factores de 12. Otra forma de verlo es que los factores de un número son los números por los cuales es divisible.

3. Use el mnemotécnico `Cómo deberíamos deshacernos de las insuficiencias` (o como un acrónimo HMWVDOA) para recordar el orden de las operaciones. A veces, simplificar una expresión es simplemente realizar las operaciones en la expresión hasta que no se puede hacer nada más. En ese caso es importante conocer el orden de las operaciones, para evitar errores de cálculo. Este mnemotécnico puede ayudarlo a recordar el orden de las ediciones: las letras corresponden al tipo de ediciones que necesita realizar y en qué orden. Si hay multiplicaciones y divisiones en el mismo problema, tendrás que realizar esas operaciones de izquierda a derecha cuando llegues a ese punto. Lo mismo ocurre con la suma y la resta. La imagen de arriba da una respuesta que no es correcta. El último paso no funcionó suma y resta de izquierda a derecha. Primero se agregó. Debe haber 25 - 20 = 5 y luego 5 + 6 = 11.
Método 2 de 4: combinar términos semejantes

1. Escribe tus ecuaciones. Las ecuaciones matemáticas más simples (aquellas con solo unas pocas variables y coeficientes como números enteros, sin fracciones, raíces cuadradas, etc.) a menudo se puede resolver en unos pocos pasos. Como con la mayoría de los problemas matemáticos, el primer paso para simplificar una ecuación es escribir la ecuación!
- Para los siguientes pasos tomamos la expresión 1 + 2x - 3 + 4x como ejemplo.

2. Determina cuáles son los términos semejantes. Ahora busca los términos semejantes en tu ecuación. Recuerda que los términos semejantes tienen la(s) misma(s) variable(s) y exponente(s).

3. Combinar términos semejantes. Ahora que ha determinado los términos similares, puede comenzar a combinarlos para simplificar su ecuación. Sumar términos (o restarlos en el caso de términos negativos) para simplificar cada conjunto de términos (con las mismas variables y exponentes) en un solo término.

4. Haz una expresión simplificada de tus términos simplificados. Después de combinar sus términos similares, construya una expresión a partir de su nuevo conjunto de términos más pequeño. Ahora debería tener una expresión más simple con un término para cada conjunto de variables y exponentes en la expresión original. Esta nueva expresión es equivalente a la primera.

5. Cumplir con el orden de las operaciones al combinar términos similares. En expresiones muy simples como las que tratamos en los ejercicios anteriores, es fácil reconocer los términos semejantes. En las expresiones más complejas, como aquellas con términos entre paréntesis, fracciones y raíces, la combinación de términos similares no será inmediatamente obvia. En esos casos, siga la secuencia de operaciones y realice las operaciones en los términos de su expresión hasta que solo le queden sumas y restas.
Método 3 de 4: factorización

1. Encuentre el máximo común divisor en la expresión. La factorización es una forma de simplificar expresiones eliminando factores que aparecen en todos los términos de la expresión. Para empezar, encuentre el máximo común divisor de todos los términos de la expresión; en otras palabras, el mayor número por el cual todos los términos de la expresión son divisibles por.
- Supongamos que tomamos la ecuación 9x + 27x - 3. Tenga en cuenta que cada término en esta ecuación es divisible por 3. Porque No de los términos es completamente divisible por otro número mayor, podemos decir que 3 es el máximo común denominador de nuestra expresión.

2. Divide los términos de la expresión por el máximo común divisor. Luego divide cada término en tu ecuación por el máximo común divisor que acabas de encontrar. Todos los términos resultantes tendrán coeficientes más pequeños que los de la expresión original.

3. Escribe tu expresión como el producto del máximo común divisor y los términos restantes. Su nueva expresión no es igual a la anterior, por lo que no es correcto decir que es la versión simplificada. Para que la nueva expresión sea igual a la anterior tendremos que tener en cuenta que se divide por el máximo común divisor. Pon tu nueva expresión entre paréntesis y escribe el máximo común divisor de la ecuación original como el coeficiente de la expresión también entre paréntesis.

4. Factorizar para simplificar fracciones. Quizás ahora se pregunte por qué la factorización es útil si la nueva expresión debe multiplicarse nuevamente después de eliminar el máximo común divisor. La factorización permite a un matemático utilizar una serie de trucos para simplificar una expresión. Uno de los trucos más fáciles utiliza el hecho de que multiplicar el numerador y el denominador de una fracción por el mismo número produce una fracción en las mismas proporciones. Vea abajo:
Método 4 de 4: aplicar simplificar

1. Simplificar fracciones dividiendo por factores iguales. Como se mencionó anteriormente, si el numerador y el denominador de una expresión tienen los mismos factores, estos factores pueden eliminarse de la fracción. A veces, esto requiere factorizar el numerador, el denominador o ambos (como fue el caso en el ejemplo anterior), mientras que en otros casos los factores compartidos son inmediatamente evidentes. Tenga en cuenta que también es posible dividir los términos individuales en el numerador por la expresión en el denominador, para obtener una expresión simplificada.
- Abordemos un ejemplo que no necesariamente requiere que los escriba para simplificar. Suponga que tiene la fracción (5x + 10x + 20)/10, puede dividir cada término en el numerador por 10 en el denominador para simplificar el todo, incluso si el "5" en 5x no mayor a 10 y no es posible elegir 10 como factor.
- Haciendo esto obtenemos ((5x)/10) + x + 2. Si queremos, podemos reescribir el primer término como (1/2)x para obtener (1/2)x + x + 2.

2. Usar raíces cuadradas para simplificar raíces. Las expresiones bajo el signo de una raíz cuadrada se llaman ecuaciones de raíz cuadrada. Puede simplificar esto determinando las raíces cuadradas (factores que en sí mismos forman una segunda potencia de un número entero), después de lo cual resta la raíz cuadrada de estos factores para eliminarlos del signo radical.

3. Sume los exponentes cuando multiplique dos términos exponenciales y réstelos cuando divida. Algunas ecuaciones algebraicas requieren multiplicar o dividir términos exponenciales. No calculas todos los términos exponenciales y no multiplicas ni divides manualmente, pero contar sumas los exponentes de cada término cuando los multiplicas juntos y ¿los tiras? cuando los compartes, ahorrándote mucho tiempo. También puede aplicar este concepto para simplificar ecuaciones con múltiples variables.
Consejos
- Recuerda que tienes que considerar estos números como positivos o negativos. Mucha gente se atasca con esto y piensa, "¿Qué señal debo poner aquí??"
- Pide ayuda si la necesitas!
- Simplificar las ecuaciones matemáticas no es fácil, pero una vez que lo dominas, puedes usarlo por el resto de tu vida.
Advertencias
- Tenga cuidado de no agregar accidentalmente algunos números adicionales, exponentes u operaciones que no pertenecen allí.
- Siempre presta atención a los términos iguales y no dejes que los exponentes te engañen.
Artículos sobre el tema. "Simplificar ecuaciones matemáticas"
Оцените, пожалуйста статью
Popular