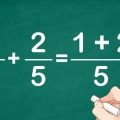Simplificar fracciones

Contenido

Pasos
Consejos

Las matemáticas no tienen por qué ser difíciles, pero no siempre es fácil recordar todos esos diferentes principios y métodos. Incluso las técnicas básicas a veces pueden olvidarse. Entonces, aquí hay dos métodos más para simplificar fracciones.

Pasos

Método 1 de 4: usar el máximo común divisor

$simplificar fracciones$

1. Haz una lista de todos los factores del numerador y el denominador. Los factores de un número dado son aquellos números que multiplicados entre sí forman ese número. Ejemplo, 3 y 4 son ambos factores de 12, porque 3 x 4 = 12. Para hacer una lista de todos los factores de un número, averigüe qué números llegan hasta ese número.

Haz una lista de los factores de menor a mayor y no olvides el 1. Esta es la lista:

24: 1, 2, 3, 4, 6, 8, 12, 24.
32: 1, 2, 4, 8, 16, 32.

$simplificar fracciones$

2. Encuentra el máximo común divisor (mcd) del numerador y el denominador. El mcd es el número más grande por el cual dos números, en este caso el numerador y el denominador, son divisibles. Una vez que tenga listas las dos listas de factores, todo lo que necesita hacer es encontrar el número más grande (el divisor) que ocurre en ambas listas.

24: 1, 2, 3, 4, 6, 8, 12, 24.

32: 1, 2, 4, 8, 16, 32.

El mcd de 24 y 32 es 8, porque 8 es el número más grande por el cual 24 y 32 son divisibles.

$simplificar fracciones$

3. Divide el numerador y el denominador por el mcd. Ahora que encontraste el mcd, todo lo que necesitas hacer es dividir el numerador y el denominador por este número para simplificar tu fracción tanto como sea posible. Así es como funciona:

24/8 = 3

32/8 = 4

entonces la fraccion simplificada es 3/4.

$simplificar fracciones$

4. Revisa tu trabajo. Si desea saber si su simplificación es correcta, multiplique el numerador y el denominador de la simplificación por el mcd para asegurarse de obtener la fracción original como resultado. Así es como funciona:

3 * 8 = 24

4 * 8 = 32

Esta es la fracción original de nuevo, 24/32.

También puedes investigar si la fracción no se puede simplificar aún más. Dado que 3 es primo, solo se puede dividir por 1 y por sí mismo, por lo que esta fracción no se puede simplificar más.

Método 2 de 4: seguir dividiendo por un número pequeño

$simplificar fracciones$

1. Elige un número pequeño. Usando este método, simplemente elija un número pequeño, como 2, 3, 4, 5 o 7, para comenzar. Mire las fracciones para asegurarse de que el número sea divisible al menos una vez por cualquier número que elija. Por ejemplo, si tomas la fracción 24/108, no elijas 5, porque no se ajusta a ninguno de los dos números. Pero, si estás investigando la fracción 25/60, entonces 5 es una excelente opción.

En el caso de la fracción 24/32, el número 2 funciona muy bien. Como ambos números son pares, también son divisibles por 2.

$simplificar fracciones$

2. Divide el numerador y el denominador de una fracción por ese número para simplificarlo. Así es como funcionó:

24/2 = 12

32/2 = 16

La nueva fracción simplificada es 12/16.

$simplificar fracciones$

3. repite esto. Como ambos números siguen siendo pares, puedes seguir dividiendo por 2. Si cualquiera de los números se vuelve impar, intente usar otro número como divisor. Así es como sigue esto:

12/2 = 6

16/2 = 8

la nueva fraccion es 6/8.

$simplificar fracciones$

4. Sigue dividiendo por 2 hasta que no puedas continuar.

6/2 = 3

8/2 = 4

la nueva fraccion sera 3/4.

$simplificar fracciones$

5. Asegúrate de que la fracción no se pueda simplificar más. Como en el ejemplo anterior: 3 es primo, por lo que ¾ no se puede simplificar más. Si el numerador y el denominador de una fracción no se pueden volver a dividir por el número elegido, pruebe con otro número.

Por ejemplo, si quieres simplificar la fracción 10/40, empiezas dividiendo el numerador y el denominador entre 5, quedando 2/8. No puedes dividir por 5 otra vez, pero puedes dividir por 2, haciendo que la respuesta final sea ¼.

$simplificar fracciones$

6. Comprueba tu respuesta. Vuelva al punto de partida multiplicando 3/4 por 2/2 tres veces y verifique si la respuesta es igual a 24/32. Aquí puedes ver esto elaborado:

3/4 * 2/2 = 6/8

6/8 * 2/2 = 12/16

12/16 * 2/2 = 24/32.

Tenga en cuenta que dividió 24/32 por 2 * 2 * 2, que es lo mismo que dividir por 8, el máximo común divisor de 24 y 32.

Método 3 de 4: Haz una lista de los divisores

$simplificar fracciones$

1. Escribe tu fracción. Deje un espacio grande en el lado derecho de su papel: se trata de escribir los factores.

$simplificar fracciones$

2. Haz una lista de los factores del numerador y el denominador. Póngalos en listas separadas. Podría ser más fácil si las listas están alineadas una encima de la otra. Comience con 1 y luego vaya de menor a mayor y escriba los pares.

Por ejemplo: tenemos la fracción 24/60. Empezar con 24.Usted nota: 24 -- 1, 2, 3, 4, 6, 8, 12, 24

Luego continúa con 60.Usted nota: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

$simplificar fracciones$

3. Encuentra el máximo común divisor (mcd).¿Cuál es el número más grande que es a la vez divisor del numerador y del denominador?? Sea lo que sea, divide ambos números por ese número.

En nuestro ejemplo, el número más grande es el divisor 12. Entonces ambos dividimos 24 y 60 por 12, haciendo que la fracción sea 2/5, nuestra fracción simplificada!

Método 4 de 4: usar factores primos

$simplificar fracciones$

1. Encuentra los factores primos del numerador y el denominador. A "número primo" es un número que no se puede dividir por ningún otro entero excepto por 1 y por sí mismo. 2, 3, 5, 7 y 11 son ejemplos de números primos.

Empezar con el contador. Divide 24 en factores 2 y 12. porque 2 es un número primo, terminaste con esa rama inmediatamente! Ahora divide 12 en factores 2 y 6. 2 es primo -- bien! Ahora divide el 6 en factores 2 y 3. Ahora tienes 2, 2, 2 y 3 como primos.
Continuar con el denominador. Divide 60 en factores 2 y 30. Divide 30 en factores 2 y 15. Dividir 15 en 3 y 5, ambos primos. Ahora tienes la siguiente lista de números primos: 2, 2, 3 y 5.

$simplificar fracciones$

2. Escribe los factores primos del numerador y el denominador. Toma la serie de números primos que has encontrado y multiplícalos juntos. Haz esto para el numerador y el denominador. Esto hace que sea más fácil ver lo que está sucediendo.

Entonces para 24 tienes 2 x 2 x 2 x 3 = 24.

Y para 60 tienes 2 x 2 x 3 x 5 = 60

$simplificar fracciones$

3. Ignorar los factores iguales. Cualquier par de números de cualquier serie se puede eliminar. En este caso tenemos dos parejas de dos y una pareja de tres. Esos se pueden quitar!

Lo que nos queda es un 2 y un 5 – o 2/5! La misma respuesta que obtuvimos con el método anterior.

Si tanto el numerador como el denominador son números pares, recuerda dividir el número por la mitad. Sigue haciéndolo hasta que sean demasiado pequeños para dividirlos más.