Desplazamiento = D El desplazamiento es la distancia que ha recorrido un objeto dado. Por lo general, la unidad de desplazamiento se indica en metros. tiempo = t Velocidad = v La velocidad vectorial es la velocidad de un objeto en una dirección particular. Al calcular la velocidad instantánea buscamos la velocidad de un objeto en un instante dado t (tiempo). La velocidad generalmente se expresa en metros por segundo (m/s). Pendiente (o "Pendiente") = metro Puede ser útil para mostrar el movimiento de un objeto en un gráfico x-y simple con el tiempo trazado a lo largo del eje x y el desplazamiento a lo largo del eje y. Entonces la pendiente de la línea en un punto determinado es la velocidad del objeto. 
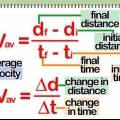
La velocidad (v) en un momento dado (t) es igual a la pendiente (tasa de cambio) de la ecuación anterior, donde el desplazamiento (d) se grafica contra el tiempo (t). 
Una regla general para encontrar la derivada: si y = a*x, entonces la derivada es a*n*x. Esta regla se aplica a cualquier término del polinomio. La constante (el número sin variable al lado) desaparecerá porque se multiplica por 0. 






Para calcular la velocidad instantánea es necesario calcular la pendiente de un gráfico para cualquier punto dado. 




El valor al que se mueve la pendiente cuando H se acerca a 0 es el límite. Esto es igual a la pendiente de la tangente a la curva. La tangente es una línea recta definida como una paralela a la parábola en una distancia infinitamente corta. La pendiente de la recta tangente es, por tanto, la pendiente de la parábola/curva si H se convierte en una distancia infinitesimal en la recta. La ecuación para encontrar la tangente es la derivada de la ecuación de la función de desplazamiento, como en la primera parte. 
Calcular la velocidad instantanea
Contenido
La velocidad vectorial (velocidad en inglés) se define como la velocidad de un objeto en una dirección particular. Para fines generales, encontrar la velocidad de un objeto es tan simple como dividir la distancia recorrida por el tiempo que tarda en recorrer esa distancia. Pero esto solo da la velocidad promedio a lo largo de un camino dado. Usando ecuaciones matemáticas y derivadas, es posible calcular la velocidad del objeto en un momento dado a lo largo de la trayectoria. Se llama velocidad instantanea. En aras de la comodidad y la legibilidad, nos referiremos a la velocidad a continuación, tanto cuando nos referimos a la velocidad "normal" como a la velocidad vectorial.
Pasos
Método 1 de 2: Cálculo de la velocidad instantánea

1. Qué "velocidad instantanea". Los objetos que se mueven pueden hacer eso con un velocidad constante – que se mueve a una velocidad constante durante todo el viaje. Un corredor que trota a lo largo de un campo de fútbol mantiene aproximadamente la misma velocidad a lo largo de todo el campo. Los objetos también pueden moverse con un velocidad variable. Por ejemplo, un automóvil que circula por una carretera con muchas curvas no tendrá la misma velocidad todo el tiempo: en las curvas la velocidad disminuye, solo para aumentar nuevamente en las rectas.
- Velocidad instantanea es una medida de la velocidad de un objeto en cualquier momento. Por ejemplo, la velocidad instantánea de un cohete, exactamente un segundo después de la ignición del propulsor, es mucho menor que su velocidad instantánea 30 segundos después del despegue, si el cohete ha tenido tiempo de ganar velocidad.

2. Conozca sus variables. Cuando se trata de cálculos de velocidad instantánea, casi siempre encontrará ciertas variables en algún momento. Estas variables son:

3. Un ejemplo. Digamos que el desplazamiento de un objeto se puede representar mediante una ecuación: desplazamiento(s) = 3t + 4t + 7. La gráfica de esta función es una línea curva o parábola, donde el eje x representa el tiempo y el eje y representa el desplazamiento.

4. Para calcular la velocidad instantánea de un objeto con un desplazamiento según la función anterior, necesitamos la derivada de esta función. La derivada de una función es igual a la pendiente de la función en cualquier punto de la gráfica. Para encontrar la derivada, diferenciamos la función según esta fórmula:

5. Usa esta fórmula para calcular la derivada de la función. Si escribimos esto como y = 3x + 4x + 7, entonces la derivada es (3*2)*x+(4*1)*x+(7*0)*x

6. Simplifica la ecuación. Multiplicando todos los términos entre paréntesis da 6x+ 4x+ 0x

7. sigue simplificando. Esta ecuación se puede escribir como 6x + 4. El "0x" entonces el término se vuelve igual a 0, mientras que el "4x" término se simplifica a 4 (n = 1.)

8. Haz que esta nueva función sea igual a la pendiente m. Usamos esta función derivada para encontrar la pendiente de la ecuación original y = 3x + 4x + 7 para cualquier valor dado de x (tiempo). La pendiente original de la ecuación en cualquier momento dado es la velocidad instantánea.

9. Encuentre la velocidad instantánea del objeto durante t = 4 segundos. Todo lo que tienes que hacer es ingresar el valor del tiempo en la variable x de la derivada de la ecuación. Esto da la siguiente ecuación y = 6(4) + 4 . Esto se simplifica a 28. La velocidad instantánea del objeto para t=4 segundos es 28 m/s.
Método 2 de 2: comprender una derivada

1. Dibujar un sistema de coordenadas x-y ordinario. Para comprender correctamente cómo una derivada puede ayudar a encontrar la velocidad instantánea de un objeto, una representación gráfica es muy útil. El eje y representa el desplazamiento del objeto, mientras que el eje x representa el tiempo.
- El gráfico puede continuar debajo del eje x. Si la línea que representa el movimiento del objeto cae por debajo del eje x, significa que el objeto se mueve en la dirección inversa y antes del punto de partida. Por lo general, el gráfico no se extenderá más allá del eje y. La velocidad no se mide para objetos que retroceden en el tiempo!
- Si no está seguro de cómo dibujar un gráfico o qué representan exactamente el eje x y el eje y, aprenda cómo puede dibujar un gráfico de una función.

2. Dibujar una línea curva, comenzando desde el punto en la línea x=0, en la dirección del eje x. La pendiente de la línea es la tasa a la que cambia y dividida por la tasa a la que cambia x. Entonces, si y es igual al desplazamiento y x es igual al tiempo, entonces la pendiente es igual a la velocidad.

3. Para encontrar la pendiente de una línea para un punto determinado, usamos un truco donde encontramos el límite de la ecuación. Encontrar el límite requiere dos puntos P y Q en una línea curva y encontrar la pendiente de la línea a través de ambos puntos a medida que la distancia entre los dos puntos se hace cada vez más pequeña.

4. Elija un punto P en la línea. Por ejemplo, coloque P en x=1. La ubicación exacta no importa. Elija un valor que sea conveniente.

5. Elija un segundo punto Q en la línea. Q debe estar a poca distancia de la P. En nuestro ejemplo, Q está en el punto con x=3, mientras que P está en el punto con x=1.

6. Encuentre la pendiente entre P y Q. La pendiente entre P y Q entonces se convierte en (la diferencia en el valor de y de P y Q)/(la diferencia en el valor de x de P y Q). Nos referimos a esta diferencia en los valores de x de P y Q como H. En este caso H es igual a 3-1=2.

7. Reducir el valor de H. En otras palabras, acerque Q a P en el eje x, luego calcule nuevamente la pendiente entre P y Q. Haga esto repetidamente, cada vez disminuyendo la distancia entre P y Q. Después de calcular esto varias veces, debería quedar claro que la pendiente se acerca a cierto valor. mientras H>0 la pendiente nunca alcanzará este valor, solo se acercará. Entonces decimos que la pendiente se acerca el limite.

8. Usa derivadas para encontrar la pendiente si H representa un intervalo infinitesimal en la recta. La derivada de una ecuación se encuentra por "x, es N*x" para aplicar a cualquier término de la ecuación original.
Consejos
- El desplazamiento es como la distancia, pero en cierta dirección, por lo que el desplazamiento es un vector y la velocidad es una cantidad escalar. El desplazamiento puede ser negativo mientras que la distancia solo puede ser positiva.
- Para encontrar la aceleración (el cambio de velocidad con el tiempo), use el método de la primera parte para encontrar la derivada de su función de desplazamiento. Luego toma la derivada de eso. Esto le da la ecuación para encontrar la aceleración en cualquier momento dado: todo lo que tiene que hacer es ingresar el valor del tiempo en esta segunda derivada.
- La ecuación que relaciona y (desplazamiento) con x (tiempo) puede ser muy simple, como por ejemplo. y = 6x + 3. En este caso la pendiente es constante y no es necesario encontrar una derivada de la pendiente. Es igual a 6, según la ecuación lineal y = mx + b.
Artículos sobre el tema. "Calcular la velocidad instantanea"
Оцените, пожалуйста статью
Popular