Instrucciones de paso a paso gratis 
En nuestro problema de ejemplo, podemos usar la ecuación de la lente para encontrar dI para decidir. Completa los valores de f y dO y resuelve: La distancia focal de una lente es la distancia desde el centro de la lente hasta el punto donde los rayos de luz convergen en un punto focal. Si alguna vez has intentado hacer un agujero en un trozo de papel con una lupa, sabes lo que significa. Este valor se da a menudo para problemas de física. En la vida real, a veces encontrará esta información marcada en la propia lente. 
En nuestro problema de ejemplo, determinamos hI como sigue: Tenga en cuenta que una altura negativa indica que la imagen que vemos está volteada. 
En nuestro ejemplo, determinamos M de la siguiente manera: También obtenemos la misma respuesta si usamos los valores d: Tenga en cuenta que la ampliación no tiene unidad. 
El tamaño. Cuanto más grande es valor absoluto de M, más se magnificará el objeto por la lente. Los valores de M entre 1 y 0 indican que el objeto aparecerá más pequeño. La orientación. Los valores negativos indican que la imagen está al revés. En nuestro ejemplo, el valor de M es -0.666, lo que significa que, bajo las condiciones dadas, la imagen de la muñeca de acción boca abajo y dos tercios del tamaño normal. 
Volvamos a examinar el problema anterior, solo que esta vez para una lente divergente con una distancia focal de -20 centímetros. Todos los demás valores iniciales son iguales. Primero determinamos dI con la comparación de lentes: Ahora determinamos hI y M con nuestro nuevo valor para dI. 
Por ejemplo: supongamos que tenemos un pequeño telescopio. Si la distancia focal del objetivo es de 10 centímetros y la distancia focal del ocular es de 5 centímetros, entonces 10/5 = 2.
Calcular ampliación
Contenido
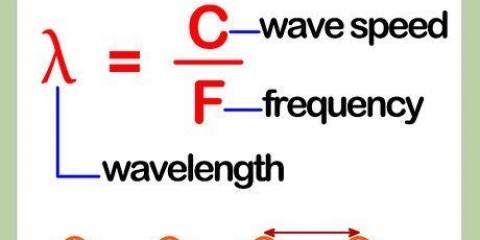
En óptica, la aumento de un objeto como una lente, la relación entre la altura de la imagen de un objeto que puede ver y su tamaño real. Por ejemplo, una lente que hace que un objeto pequeño parezca grande tiene una fuerte aumento, mientras que una lente que hace que un objeto parezca más pequeño es un débil el aumento tiene. La magnificación de un objeto generalmente viene dada por la fórmula M = (hI/ horaO) = -(dI/DO), donde M = aumento, hI = altura de la imagen, hO = altura del objeto, y dI ydO = distancia de la imagen y distancia del objeto.
Pasos
Método 1 de 2: determinar el tamaño de una sola lente
No hay té lentes convergentes es más ancho en el centro que en el borde (como una lupa). A lente divergente es más ancho en el borde y más delgado en el medio (como un tazón). Las mismas reglas se aplican a ambos cuando se trata de determinar la ampliación, con una excepción importante, como verá a continuación.
1. Tome la ecuación/fórmula como punto de partida y determine qué datos tiene. Al igual que con otros problemas de física, un buen enfoque es escribir primero la ecuación que necesita. Entonces puedes empezar a buscar las piezas que faltan en la ecuación.
- Por ejemplo, supongamos que un muñeco de acción de 6 centímetros está a medio metro de un lentes convergentes con una distancia focal de 20 centímetros se coloca. Si hacemos el aumento, tamaño de la imagen y distancia de la imagen queremos determinar, entonces comenzamos escribiendo la ecuación:
- M = (hI/ horaO) = -(dI/DO)
- En este punto sabemos hO (la altura de la muñeca de acción) y dO (la distancia desde la muñeca de acción hasta la lente.) También conocemos la distancia focal de la lente, que no está incluida en la ecuación. lo haremos ahora hI, DI y M necesito encontrar.
2. Usa la comparación de lentes para encontrar dI para decidir. Si conoce la distancia del objeto que está ampliando desde la lente y la distancia focal de la lente, determinar la distancia de la imagen es fácil usando la ecuación de la lente. La ecuación de la lente es 1/f = 1/dO + 1/díaI, donde f = la distancia focal de la lente.
- 1/f = 1/dO + 1/díaI
- 1/20 = 1/50 + 1/díaI
- 5/100 - 2/100 = 1/díaI
- 3/100 = 1/díaI
- 100/3 = reI = 33.3 centímetros
3. Resolver para hI. sabes dO ydI, entonces puede encontrar la altura de la imagen ampliada y la ampliación de la lente. Observe los dos signos de igual en la ecuación (M = (hI/ horaO) = -(dI/DO)) — esto significa que todos los términos son iguales entre sí, por lo que ahora tenemos M y hI ser capaz de determinar, en cualquier orden.
- (hI/ horaO) = -(dI/DO)
- (hI/6) = -(33.3/50)
- hI = -(33.3/50) × 6
- hI = -3.996cm
4. Resolver para M. Ahora puede resolver la última variable con -(dI/DO) o con (hI/ horaO).
- M = (hI/ horaO)
- M = (-3.996/6) = -0.666
- M = -(dI/DO)
- METRO = -(33.3/50) = -0.666
5. Interpretar el valor de M. Una vez que haya encontrado la ampliación, puede predecir diferentes cosas sobre la imagen que verá a través de la lente. Estos son:
6. Para lentes divergentes, use una distancia focal negativa. Aunque las lentes divergentes se ven muy diferentes a las lentes convergentes, puede determinar su aumento utilizando las mismas fórmulas mencionadas anteriormente. La única excepción significativa es que lentes divergentes tienen una distancia focal negativa tener. En un problema similar al indicado anteriormente, esto afectará el valor de dI, así que asegúrate de prestar atención a eso.
- 1/f = 1/dO + 1/díaI
- 1/-20 = 1/50 + 1/díaI
- -5/100 - 2/100 = 1/díaI
- -7/100 = 1/díaI
- -100/7 = reI = -14.29 centímetros
- (hI/ horaO) = -(dI/DO)
- (hI/6) = -(-14.29/50)
- hI = -(-14.29/50) × 6
- hI = 1.71 centímetros
- M = (hI/ horaO)
- METRO = (1.71/6) = 0.285
Método 2 de 2: determinar la ampliación de varias lentes seguidas
Método de dos lentes
1. Determine la distancia focal para ambas lentes. Cuando se trata de un dispositivo que usa dos lentes seguidas (como en un telescopio o parte de un par de binoculares), todo lo que necesita saber es la distancia focal de ambas lentes para obtener la ampliación final de la imagen. determinar. Haces esto con la ecuación simple M = fO/Fmi.
- En la ecuación f se refiereO a la distancia focal de la lente y fmi a la distancia focal del ocular. El objetivo es la lente grande al final del dispositivo, mientras que el ocular es la parte por la que miras.
2. Usa estos datos en la ecuación M = fO/Fmi. Una vez que haya encontrado la distancia focal para ambas lentes, resolver el problema se vuelve fácil; encuentras la relación dividiendo la distancia focal del objetivo por la del ocular. La respuesta es la ampliación del dispositivo.
método detallado
- Por ejemplo, supongamos que tenemos la misma configuración que en el ejemplo del Método 1: un objeto de 6 centímetros a una distancia de 50 centímetros de una lente convergente con una distancia focal de 20 centímetros. Ahora colocamos una segunda lente convergente con una distancia focal de 5 centímetros detrás de la primera lente (a 100 centímetros de la muñeca de acción).) En los siguientes pasos usaremos esta información para encontrar la ampliación de la imagen final.
- De nuestro trabajo en el Método 1, sabemos que la primera lente produce una imagen de -3.996 centímetros alto, 33.3 centímetros detrás de la lente, y con un aumento de -0.666.
- En nuestro ejemplo esto es 50-33.3 = dieciséis.7 centímetros para el segundo, porque la imagen 33.3 centímetros detrás de la primera lente. Usemos esto, junto con la distancia focal de la nueva lente, para encontrar la imagen de la segunda lente.
- 1/f = 1/dO + 1/díaI
- 1/5 = 1/16.7 + 1/díaI
- 0.2 - 0.0599 = 1/díaI
- 0.14 = 1/díaI
- DI= 7.14 centímetros
- Ahora podemos hI y calcule M para la segunda lente:
- (hI/ horaO) = -(dI/DO)
- (hI/-3.996) = -(7.14/16.7)
- hI = -(0.427) × -3.996
- hI = 1.71 centímetros
- M = (hI/ horaO)
- METRO = (1.71/-3.996) = -0.428
- No olvides que los siguientes lentes pueden volver a invertir tu imagen. Por ejemplo, la ampliación que calculamos anteriormente (-0,428) indica que la imagen tiene aproximadamente 4/10 del tamaño de la imagen de la primera lente, pero en posición vertical, porque la imagen de la primera lente estaba invertida.
1. Determine la distancia entre las lentes y el objeto. Si coloca dos lentes frente a un objeto, es posible determinar la ampliación de la imagen final, siempre que conozca la relación entre la distancia de las lentes al objeto, el tamaño del objeto y la distancia focal de la objeto ambas lentes. Todo lo demás que puedas distraer.
2. Determine la distancia, la altura y el aumento de la imagen para la lente número 1. La primera parte de cualquier problema que involucre múltiples lentes es la misma que la de aquellos que involucran solo una lente. Comience con la lente más cercana al objeto y use la ecuación de la lente para encontrar la distancia desde la imagen; Ahora usa la ecuación de magnificación para encontrar la altura y la magnificación de la imagen.
3. Usar la imagen del primero como objeto para el segundo. Ahora determinando el aumento, la altura, etc. para la segunda lente fácil; solo use las mismas técnicas que usó para la primera lente. Solo que esta vez usas la imagen en lugar del objeto. Recuerde que la imagen generalmente estará a una distancia diferente de la segunda lente en comparación con la distancia entre el objeto y la primera lente.
4. Continúe así con cualquier lente adicional. El enfoque estándar es el mismo ya sea que coloque 3, 4 o 100 lentes en una fila para un objeto. Para cada lente, considere la imagen de la lente anterior como el objeto y luego use la ecuación de la lente y la ecuación de aumento para calcular la respuesta.
Consejos
- Los binoculares generalmente se indican mediante una multiplicación de dos números. Por ejemplo, los binoculares pueden etiquetarse como 8x25 u 8x40. El primer número es el aumento de los binoculares. El segundo número es la nitidez de la imagen.
- Tenga en cuenta que una ampliación con una sola lente, esta ampliación es un número negativo si la distancia al objeto es mayor que la distancia focal de la lente. Esto no quiere decir que el objeto parezca más pequeño, sino que la imagen se percibirá al revés.
Artículos sobre el tema. "Calcular ampliación"
Оцените, пожалуйста статью
Popular
