Centro del balancín = 4 metros desde el punto cero. Niño 1=1 metro de distancia del punto cero Niño 2=5 metros del punto cero 



430 m*kg ÷ 130 kilos=3,31 m El centro de gravedad está a 3,31 metros del punto cero, o medido desde el punto cero, está a 3,31 metros del extremo del lado izquierdo del balancín donde se colocó el punto cero. 



La forma en que lo resolvimos, el cero está en el lado izquierdo del balancín. Nuestra respuesta es 3,31 m, por lo que nuestro centro de masa está a 3,31 m del cero de la izquierda. Si elige un nuevo punto cero, 1 m desde la izquierda, obtiene como respuesta 2,31 m desde el centro de masa. El centro de masa está a 2,31 m desde el nuevo punto cero, es decir, 1 m desde la izquierda. El centro de masa es 2,31 + 1=3,31 m desde la izquierda, y por lo tanto la misma respuesta que calculamos antes. (Nota: al medir la distancia, recuerde que las distancias izquierda desde el punto cero son negativas, y las distancias derecho de eso positivo.) 
En los problemas de balancín, lo único que importa es dónde está el centro de gravedad de izquierda a derecha a lo largo de la línea del balancín. Más adelante puede aprender formas más avanzadas de calcular el centro de gravedad en dos dimensiones.
Calcular el centro de gravedad
Contenido
El centro de gravedad (el centro de masa) es el centro de distribución del peso de un objeto, el punto donde la gravedad actúa sobre ese objeto. Este es el punto donde el objeto está en perfecto equilibrio, sin importar cómo se tuerza o gire el objeto alrededor de ese punto. Si desea saber cómo calcular el centro de gravedad de un objeto, necesita el peso del objeto y de todos los objetos en él. Luego determinas un cero y procesas las cantidades conocidas en la ecuación, para calcular el centro de gravedad de un objeto o sistema. Si quieres saber cómo calcular el centro de gravedad, sigue los siguientes pasos.
Pasos
Método 1 de 4: determinar el peso

1. Calcular el peso del objeto. Al calcular el centro de gravedad, primero deberá averiguar el peso del objeto. Digamos que quieres calcular el peso de un balancín con una masa de 30 kilos. Como es un objeto simétrico, su centro de gravedad estará exactamente en el medio (si nadie está sentado sobre él). Pero si hay personas con diferentes masas en el balancín, entonces el problema se vuelve un poco más complicado.

2. Calcular los pesos extra. Para determinar el centro de gravedad del balancín con dos niños, deberá determinar el peso individual de cada niño. El primer niño tiene una masa de 40 kilos y el segundo niño es de 60 kilos.
Método 2 de 4: determinar el punto cero

1. Elige un punto cero. El punto cero es cualquier punto de partida en un lado del balancín. Puedes colocar el cero en un lado del balancín o en el otro lado. Digamos que el balancín mide 6 metros de largo. Pongamos el cero en el lado izquierdo del balancín, cerca del primer niño.

2. Mida la distancia desde el punto cero hasta el centro del objeto principal, así como hasta los dos pesos adicionales. Digamos que los niños están a 1 metro de cada extremo del balancín. El centro del balancín es el centro del balancín, o 3 metros, porque 6 metros divididos por 2 es igual a 3. Aquí están las distancias desde el centro del objeto más grande y los dos pesos adicionales forman el punto cero:
Método 3 de 4: determinar el centro de gravedad

1. Multiplique la distancia de cada objeto al punto cero por su peso para encontrar el momento. Esto le da el momento para cada objeto. He aquí cómo multiplicar la distancia de cada objeto desde el punto cero por su peso:
- El balancín: 30 kilo x 3 m=90 m*kg.
- Niño 1=40 kilo x 1 m=40 m*kg.
- Niño 2=60 kilos x 5 m=300 m*kg.

2. Suma los tres momentos juntos. Solo calcula lo siguiente: 90 m*kg + 40 m*kg + 300 m*kg=430 m*kg. El momento total es de 430 m*kg.

3. Sume los pesos de todos los objetos juntos. Encuentra la suma de los pesos del balancín y los dos niños. Haz esto de la siguiente manera: 30 kilos + 40 kilos + 60 kilos = 130 kilos.

4. Divide el momento total por el peso total. Obtiene la distancia desde el punto cero hasta el centro de gravedad del objeto. Esto al dividir 430 m * kg por 130 kilos.
Método 4 de 4: verifica tu respuesta

1. Encuentre el centro de gravedad en el diagrama. Si el centro de gravedad que ha encontrado está fuera del sistema de objetos, entonces ha encontrado la respuesta incorrecta. Tal vez has calculado la distancia desde más de un punto. Inténtalo de nuevo con solo un punto cero.
- Por ejemplo, para las personas sentadas en el balancín, el centro de gravedad debe estar en algún lugar del balancín, no a la izquierda ni a la derecha del balancín. No tiene que ser en una persona.
- Esto también se aplica a problemas en dos dimensiones. Dibuja un cuadrado lo suficientemente grande como para que quepan todos los objetos en tu problema. El centro de gravedad debe estar dentro de este cuadrado.

2. Revisa tus cálculos si tu respuesta es demasiado pequeña. Si elige un extremo del sistema como su cero, entonces una pequeña respuesta coloca el centroide justo al lado de un extremo. Esta puede ser la respuesta correcta, pero a menudo es una indicación de que algo salió mal. ¿Tienes el peso y la distancia entre sí en el cálculo? multiplicado? Esa es la manera correcta de encontrar este momento. Si accidentalmente agregado junto, entonces probablemente obtendrás una respuesta mucho más pequeña.

3. Comprueba tu cálculo si has encontrado más de un centro de gravedad. Cada sistema tiene un solo centro de gravedad. Si hay más, es posible que te hayas saltado el paso en el que tenías que sumar todos los momentos juntos. El centro de gravedad es total momento dividido por el total peso. Usted no tiene que cada momento para compartir por cada peso, que solo te da la posición de cada objeto.

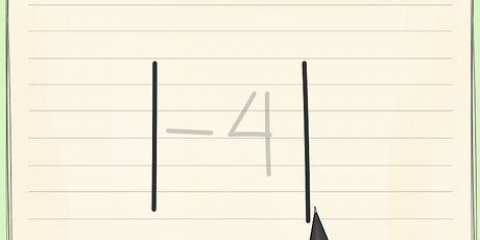
4. Marque el cero si su respuesta es un número entero apagado. La respuesta en nuestro ejemplo es 3,31 m Suponga que le dan 2,31 m, 4,31 m o algún otro número que termine en `.31.Esto probablemente se deba a que elegimos el extremo izquierdo del balancín como el cero, mientras que elegimos el extremo derecho u otro punto a una distancia entera de nuestro cero. Tu respuesta es correcta, independientemente del cero que elijas! solo tienes que recordar eso el cero siempre representa x=0. Aquí hay un ejemplo:

5. Asegúrate de que todas tus medidas sean líneas rectas. Suponga que ve otro ejemplo con "niños en un balancín", pero un niño es mucho más grande que el otro, o un niño cuelga debajo del balancín, en lugar de sentarse en él. Ignore la diferencia y tome todas sus medidas a lo largo de la línea recta del balancín. Medir distancias en ángulo arrojará respuestas cercanas, pero ligeramente diferentes.
Consejos
- Para determinar la distancia que tiene que moverse una persona para equilibrar el balancín sobre el soporte, utilice esta fórmula: (mueve peso) / (peso total)=(distancia sobre la cual se ha movido el centro de gravedad) / (distancia sobre la cual se ha movido el peso). Esta fórmula se puede reescribir para mostrar que la distancia que debe moverse el peso (la persona) es igual a la distancia entre el centro de gravedad y el fulcro, multiplicada por el peso de la persona dividido por el peso total. Así debe ser el primer hijo -1,31 m *40 kilos / 130 kilos=-0.moverse 40 m (hasta el final del balancín). ¿O debería el segundo hijo -1.08m *130 kilos / 60 kilos=-2.mover 84 m. (al centro del balancín).
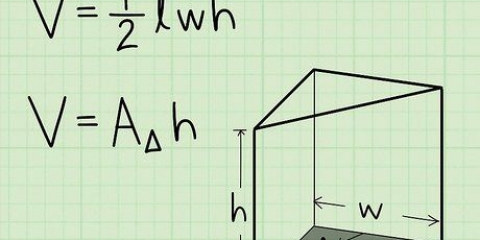
- Para encontrar el centroide de un objeto bidimensional, use la fórmula Xcg=∑xW/∑W para encontrar el centroide a lo largo del eje x, y Ycg=∑yW/∑W para encontrar el centroide a lo largo del eje y para encontrar. El punto en el que se cruzan es el centro de gravedad.
- La definición del centroide de una distribución de masa general es (∫ r dW/∫ dW) donde dW es igual a la derivada del peso, r es el vector de posición, y donde las integrales deben interpretarse como integrales de Stieltjes sobre la totalidad cuerpo. Sin embargo, se pueden expresar como integrales de volumen de Riemann o Lebesgue más convencionales para distribuciones con una función de densidad de probabilidad. A partir de esta definición, todas las propiedades del centroide, incluidas las utilizadas en este artículo, se pueden derivar de las propiedades de las integrales de Stieltjes.
Advertencias
- No intentes aplicar estas mecánicas a ciegas sin comprender la teoría, lo que puede conducir a errores. Primero intente comprender las leyes/teorías subyacentes.
Artículos sobre el tema. "Calcular el centro de gravedad"
Оцените, пожалуйста статью
Popular