No utilice libras u otras unidades que no sean estándar o la respuesta final no estará en julios. 
Si el objeto se mueve horizontalmente, entonces la gravedad es irrelevante. En cambio, el problema puede solicitar calcular la fuerza requerida para superar la resistencia por fricción. Si se da cuál es la aceleración del objeto cuando se empuja, entonces puedes multiplicar la aceleración dada por la masa. 



Si ya se proporciona una fuerza `hacia la derecha`, `arriba` o `en la dirección del movimiento`, entonces se calcula `fuerza x cos(θ)`, y puede proceder a multiplicar los valores. 
En nuestro ejemplo, el ángulo θ entre el suelo y la cuerda es de 30º. Calcular cos(θ). cos(30º)=(√3)/2=alrededor de 0,866. Puede usar una calculadora para encontrar este valor, pero asegúrese de que su calculadora use la unidad correcta cuando se da el ángulo (grados o radianes). Multiplique la potencia total x cos(θ). En nuestro ejemplo, 10N x 0,866=8,66 N en la dirección del movimiento. 



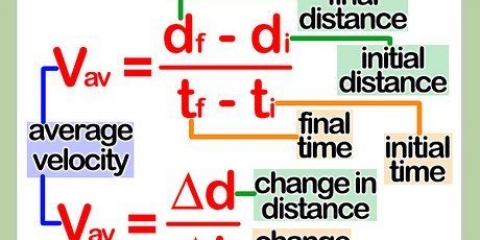
Si el ciclista se mueve a una velocidad constante (sin aceleración), mida la distancia que ha recorrido el ciclista y divídala por la cantidad de segundos que tardó en cubrir esa distancia. Esto calcula la velocidad promedio, que en este escenario es la misma que la velocidad en cualquier momento dado. Si el ciclista se mueve con una aceleración constante y no cambia de dirección, calcule su velocidad en ese momento t con la fórmula `velocidad(tiempo t)=(aceleración)(t) + velocidad inicial. El tiempo es en segundos, la velocidad en metros/segundo y la aceleración en m/s. 
La fórmula para la energía cinética se puede derivar de la definición de trabajo, W=FΔs, y la ecuación v=v0 + 2aΔs. Δs se refiere a `desplazamiento`, o también a la distancia recorrida. 







Debido a que el julio es una unidad pequeña y a que el consumo de energía de los electrodomésticos generalmente se indica en vatios, milivatios y kilovatios, a menudo es más conveniente calcular la cantidad de kWh (kilovatios hora) que consume un dispositivo. 1 vatio equivale a 1 julio por segundo, o 1 julio equivale a 1 vatio por segundo; un kilovatio es igual a 1 kilojulio por segundo y un kilojulio es igual a 1 kilovatio segundo. Hay 3600 segundos en una hora, por lo que 1 kilovatio-hora es igual a 3600 kilovatios-segundo, 3600 kilojulios o 3.600.000 julios. 

El calor específico varía ligeramente dependiendo de la temperatura y la presión. Diferentes organizaciones y libros de texto usan diferentes `temperaturas estándar`, por lo que es posible que deba usar 4 calores específicos para el calor específico del agua.179 hallazgos. También puedes usar Kelvin en lugar de Celsius, ya que 1 grado es lo mismo para ambas escalas (calentar algo a 3ºC es lo mismo que calentar algo a 3 Kelvin). No use Fahrenheit o el resultado no se dará en Joules. 

Si desea saber la cantidad total de energía almacenada en forma de calor, puede suponer que la temperatura inicial era el cero absoluto: 0 Kelvin o -273.15ºC. 

El calor generalmente se expresa en calorías o kilocalorías. Una caloría se define como la cantidad de calor requerida para elevar la temperatura de 1 gramo de agua en 1 grado Celsius, mientras que una kilocaloría (o Caloría) es la cantidad de calor requerida para elevar la temperatura de 1 kilogramo de agua en 1 grado Celsius. En el ejemplo anterior, aumentar la temperatura de 500 gramos de agua en 20 grados centígrados toma 10.000 calorías o 10 kilocalorías.
Calcular julios
Contenido
El julio (J), llamado así por el físico inglés James Edward Joule, es una de las unidades más importantes del Sistema Métrico Internacional. El joule se utiliza como unidad de trabajo, energía y calor y es ampliamente utilizado en la ciencia. Si desea que su respuesta esté en julios, utilice siempre las unidades científicas estándar.
Pasos
Método 1 de 4: calcular el trabajo en julios

1. La definición de trabajo. El trabajo se define como una fuerza constante ejercida sobre un objeto para moverlo una cierta distancia. Si no se aplica más de una fuerza, entonces se puede calcular como energía X distancia, y se puede escribir en unidades de Julios (equivalente a un `Newton metro`). En nuestro primer ejemplo, tomamos a una persona que quiere agregar un peso desde el piso hasta la altura del pecho y calculamos cuánto trabajo ha hecho esa persona.
- La fuerza debe aplicarse en la dirección del movimiento. Al sostener un objeto y caminar hacia adelante, no se realiza ningún trabajo sobre el objeto porque no se está empujando el objeto en la dirección de su movimiento.

2. Determinar la masa del objeto que se mueve. Se necesita la masa de un objeto para calcular la fuerza necesaria para moverlo. En nuestro ejemplo asumimos que el peso tiene una masa de 10 kg.

3. Calcular la fuerza. Fuerza=masa x aceleracion. En nuestro ejemplo, levantando un peso hacia arriba, la aceleración que estamos tratando de superar es igual a la gravedad, 9.8 m/s hacia abajo. Calcula la fuerza requerida para levantar el peso usando (10 kg) x (9.8 m/s)=98 kg m/s=98 Newton (N).

4. Medir la distancia que se mueve el objeto. En este ejemplo, digamos que el peso es 1.5 metros (m) se levanta. La distancia debe medirse en metros, de lo contrario la respuesta final no puede escribirse en Joules.

5. Multiplica la potencia por la distancia. A un peso de 98 Newtons 1.5 metros, serás 98 x 1.5 = 147 julios de trabajo por hacer.

6. Calcular el trabajo de los objetos que se mueven en ángulo. Nuestro ejemplo anterior era simple: alguien aplicó una fuerza hacia arriba sobre el objeto y el objeto subió. A veces, la dirección de la fuerza y el movimiento del objeto no son exactamente iguales porque hay múltiples fuerzas que actúan sobre el objeto. En el siguiente ejemplo, vamos a calcular cuántos Joules se necesitan para remolcar un trineo 25 metros por la nieve, tirando de una cuerda atada al trineo en un ángulo de 30º con la horizontal. Se aplica lo siguiente: trabajo = fuerza x cos(θ) x distancia. El símbolo θ es la letra griega `theta` y representa el ángulo entre la dirección de la fuerza y la dirección del movimiento.

7. Determine la fuerza total aplicada. En este problema, suponemos que alguien tira de la cuerda con una fuerza de 10 Newtons.

8. Calcular la fuerza relevante. Solo una parte de la fuerza tira del carro hacia adelante. Dado que la cuerda está inclinada hacia arriba, la fuerza restante intenta levantar el trineo, contrarrestando la gravedad. Calcular la fuerza en la dirección del movimiento:

9. Multiplica fuerza x distancia. Ahora que sabemos cuánta fuerza se aplica en la dirección del movimiento, podemos calcular el trabajo como de costumbre. Nuestro problema nos dice que el carro ha sido arrastrado 20 metros hacia adelante, por lo que calculamos 8,66 N x 20 m = 173,2 julios de trabajo.
Método 2 de 4: Cálculo de la energía cinética en julios

1. Entender qué energía cinética. La energía cinética es la cantidad de energía en forma de movimiento. Como con cualquier forma de energía, esto se puede expresar en Joules.
- La energía cinética es igual a la cantidad de trabajo realizado para acelerar un objeto estacionario a una velocidad dada. Una vez que se alcanza esa velocidad, el objeto retiene esa cantidad de energía cinética hasta que esa energía se convierte en calor (por fricción), energía gravitatoria (al ir contra la gravedad) u otros tipos de energía.

2. Determinar la masa del objeto. Por ejemplo, podemos medir la energía cinética de una bicicleta y un ciclista. Supongamos que el ciclista tiene una masa de 50 kg y la bicicleta una masa de 20 kg. Que se suma una masa total metro desde 70kg. Ahora podemos tratarlos juntos como 1 objeto de 70 kg, porque se mueven juntos a la misma velocidad.

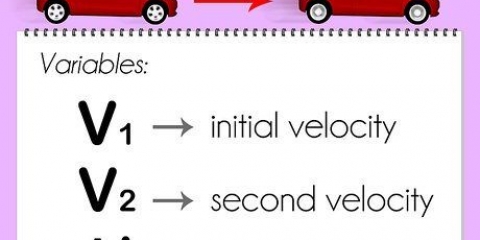
3. Calcular la velocidad. Si ya conoces la velocidad o el vector de velocidad del ciclista, anótalo y sigue adelante. Si aún tiene que calcular esto, use uno de los métodos a continuación. Esta es la velocidad, no la velocidad vectorial (que es la velocidad en una determinada dirección), aunque la letra se usa a menudo como abreviatura v utilizado para la velocidad. Ignora cualquier giro que haga el ciclista y finge que toda la distancia se cubre en línea recta.

4. Ingrese los siguientes números en la siguiente fórmula. Energía cinética=(1/2)metro`v. Por ejemplo, si el ciclista se mueve a una velocidad de 15 m/s, entonces su energía cinética es K=(1/2)(70 kg)(15 m/s)=(1/2)(70 kg)( 15 m/s)(15 m/s)=7875 kgm/s=7875 newton metros=7875 julios.
Método 3 de 4: calcular el julio como energía eléctrica

1. Calcular energía usando potencia x tiempo. La potencia se define como la energía consumida por unidad de tiempo, por lo que podemos calcular la energía consumida por la potencia multiplicada por la unidad de tiempo. Esto es útil cuando se mide la potencia en vatios, porque 1 vatio = 1 julio/segundo. Para saber cuánta energía usa una bombilla de 60 W en 120 segundos, multiplique lo siguiente: (60 vatios) x (120 segundos) = 7200 julios.
- Esta fórmula se puede utilizar para cualquier tipo de potencia, medida en vatios, pero la electricidad es la más obvia.

2. Use los pasos a continuación para calcular el flujo de energía en un circuito eléctrico. Los pasos a continuación están escritos como un ejemplo práctico, pero también puede usar este método para comprender problemas de física teórica. Primero calculamos la potencia P usando la fórmula P=I x R, donde I es la corriente en amperios y R es la resistencia en ohmios. Estas unidades nos dan la potencia en vatios, por lo que a partir de aquí podemos aplicar la fórmula utilizada en el paso anterior para calcular la energía en julios.

3. Elige una resistencia. Las resistencias se indican en ohmios, con su valor indicado directamente en la resistencia, o indicado por una serie de anillos de colores. También puede probar una resistencia con un ohmímetro o un multímetro. En este ejemplo, asumimos que la resistencia que estamos usando es de 10 ohmios.

4. Conecte la resistencia a una fuente de alimentación (batería). Use abrazaderas para esto o coloque la resistencia en un circuito de prueba.

5. Deje que una corriente fluya a través de él durante un cierto período de tiempo. En este ejemplo tomamos 10 segundos como unidad de tiempo.

6. Medir la fuerza de la corriente. Haces esto con un medidor de electricidad o un multímetro. La mayoría de las formas de corriente doméstica van en miliamperios, así que supongamos que la corriente es de 100 miliamperios o 0,1 amperios.

7. Usa la fórmula P=I x R. Ahora para encontrar la potencia, multiplique la potencia de la corriente por la resistencia. Esto le da la potencia de este circuito en vatios. El cuadrado de 0.1 da 0.01. Multiplique esto por 10 y obtendrá una potencia de salida de 0,1 vatios o 100 milivatios.

8. Multiplica la potencia por el tiempo transcurrido. Esto produce la energía en julios. 0,1 vatios x 10 segundos equivale a 1 julio de energía eléctrica.
Método 4 de 4: Cálculo del calor en julios

1. Determine la masa del objeto al que se le agrega calor. Use una balanza o balanza para esto. Si el objeto es un líquido, primero pesa el recipiente vacío en el que va el líquido. Deberá restar esto de la masa del recipiente y del líquido para encontrar la masa del líquido. En este ejemplo asumimos que el objeto son 500 gramos de agua.
- Use gramos, no otra unidad, de lo contrario el resultado no se dará en Joules.

2. Determinar el calor específico del objeto. Esta información se puede encontrar en los libros de referencia de química de binas, pero también se puede encontrar en línea. Para el agua, el calor específico C es igual a 4.19 julios por gramo por cada grado Celsius, o 4.1855, si quieres ser muy preciso.

3. Determinar la temperatura actual del objeto. Si el objeto es un líquido, puede usar un termómetro normal (de mercurio). Para otros objetos puede necesitar un termómetro con sonda.

4. Caliente el objeto y mida la temperatura nuevamente. Esto le permite medir la cantidad de calor agregado a un objeto durante el calentamiento.

5. Reste la temperatura original de la temperatura después de calentar. Esto resulta en el cambio en la temperatura del objeto. Suponiendo que el agua estaba inicialmente a 15 grados centígrados y después de calentarla a 35 grados centígrados, el cambio de temperatura es de 20 grados centígrados.

6. Multiplique la masa del objeto por el calor específico y el cambio de temperatura. Escribes esta fórmula como H=mcΔt, donde ΔT representa el `cambio de temperatura`. En este ejemplo, serán 500 g x 4.19x20=41.900 julios.
Consejos
- Relacionado con el julio hay otra unidad de trabajo y energía llamada ergio; 1 erg es igual a 1 dina de fuerza por una distancia de 1 cm. Un julio es igual a 10.000.000 ergio.
Advertencias
- Aunque los términos `julio` y `newton metro` se refieren a la misma unidad, en la práctica el `julio` se usa para indicar cualquier forma de energía y para el trabajo realizado en línea recta, como en el ejemplo anterior de subir escaleras. Cuando se usa para calcular el par (fuerza sobre un objeto giratorio), preferimos el término `newton metro`.
Artículos de primera necesidad
Cálculo de trabajo o energía cinética:
- Cronómetro o un temporizador
- Libra o Equilibrio
- Calculadora con función coseno (solo para el trabajo, no siempre es necesario)
Cálculo de la energía eléctrica:
- Resistencia
- Cables o una placa de prueba
- Multímetro (o un ohmímetro y un medidor de corriente)
- Fahnestock o pinzas de cocodrilo
Calor:
- Objeto a calentar
- Fuente de calor (como un mechero Bunsen)
- Termómetro (un termómetro de líquido o un termómetro con sonda)
- Química/referencia química (para encontrar el calor específico del objeto que se está calentando)
Artículos sobre el tema. "Calcular julios"
Оцените, пожалуйста статью
Popular