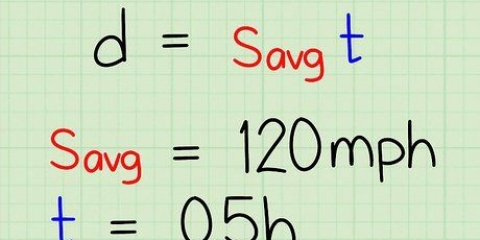En nuestro ejemplo, digamos que es exactamente dos en punto costo de hacer este viaje. 
En nuestro ejemplo, esta ecuación es 100 millas/2 horas = 50 millas/hora(unos 80 km/h). 
Las unidades de velocidad son las unidades de distancia sobre las unidades de tiempo. En nuestro ejemplo, nuestras unidades son millas/hora (o millas por hora) ya que medimos la distancia en millas y el tiempo en horas. 

Por ejemplo, digamos que en el problema de ejemplo anterior necesitamos nuestra respuesta en millas en vez de kilómetros. Hay alrededor de 1,6 kilómetros en una milla, por lo que podemos convertirlo así: Tenga en cuenta que debido a que los kilómetros están al final de la fracción, se pueden tachar con los kilómetros en la respuesta original, dejando la respuesta en millas. Éste el sitio contiene conversiones para las unidades más comunes. 
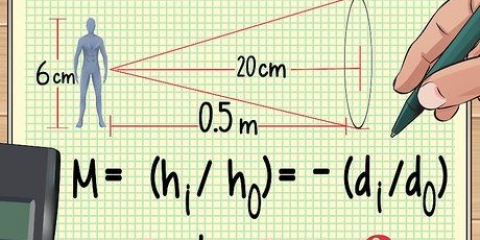
Por ejemplo, digamos que un avión vuela cinco veces en un círculo de 20 millas de ancho. El avión completa este trayecto en media hora. En este ejemplo, todavía necesitamos determinar exactamente qué tan lejos ha viajado el avión antes de que podamos encontrar la velocidad. Podemos usar la ecuación para la distancia alrededor de un círculo (su circunferencia) en lugar de "a" en nuestra comparación. Esta ecuación es circunferencia = 2πr donde r = el radio del círculo. Podemos resolver esto de la siguiente manera: 
Para ilustrar esta diferencia, imagina el último viaje que hiciste en coche. Es muy poco probable que haya viajado a la misma velocidad durante todo el viaje. En cambio, comenzó despacio y gradualmente alcanzó su velocidad máxima y disminuyó la velocidad en los semáforos, embotellamientos, etc. Si usa la ecuación de velocidad estándar para calcular su velocidad para el viaje, estos cambios de velocidad no se reflejan. En su lugar, obtendrá una respuesta en algún lugar entre las diferentes velocidades a las que ha viajado. 

Por esta razón, ambos autos en el problema de ejemplo anterior tienen un velocidad (velocidad) por 50 km/h. 
Suponga que la posición de un objeto en metros está dada por la ecuación 3t + t - 4 donde t = tiempo en segundos. Queremos saber cuál es la velocidad del objeto en t = 4 segundos. En este caso, podemos resolver esto de la siguiente manera: Ahora llenamos t = 4: 
Supongamos que un objeto tiene una aceleración constante (en m/s dada por a (t) = -30. Digamos también que el objeto tiene una velocidad inicial de 10 m/s. Necesitamos encontrar la velocidad en t = 12s. En este caso, podemos resolver esto de la siguiente manera: Para encontrar C, resolvemos para v(t) para t = 0. Recuerda que la velocidad inicial del objeto es de 10 m/s. Ahora podemos ingresar t = 12 segundos.
Calcular velocidad
Contenido
La velocidad es la medida de `qué tan rápido` va algo en un momento dado. Si alguna vez ha mirado el velocímetro de un automóvil mientras conduce, ha visto cómo se mide la velocidad: cuanto más avanza la aguja, más rápida es la velocidad del automóvil. Hay algunas formas diferentes de calcular la velocidad, dependiendo de la información que tenga. Para propósitos generales, la ecuación es velocidad = distancia/tiempo (o s = a/t) generalmente la forma más fácil de calcular la velocidad.
Pasos
Método 1 de 3: usar la ecuación de velocidad estándar

1. Encuentra la distancia que ha viajado un objeto. La ecuación básica que la mayoría de la gente usa para averiguar qué tan rápido va algo es muy fácil de usar. Lo primero que debes saber es la distancia que ha recorrido el objeto. En otras palabras, ¿a qué distancia está el punto de inicio del punto final??
- Esta ecuación será más fácil de entender con un ejemplo. Digamos que damos un paseo en automóvil a un parque temático de 100 millas (alrededor de 161 kilómetros). En los próximos pasos usaremos esta información para resolver esta ecuación.

2. Encuentre el tiempo que tardó el objeto en recorrer esa distancia. La siguiente información que necesita es cuánto tiempo tardó el objeto en viajar. En otras palabras, ¿cuánto tiempo tardó en llegar desde el punto de inicio hasta el punto final??

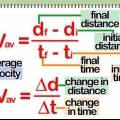
3. Divide la distancia entre el tiempo para encontrar la velocidad. Todo lo que necesita son estos dos datos para determinar su velocidad para el viaje. La distancia acerca de el tiempo te da la velocidad del objeto.

4. No olvides las unidades. Etiqueta tu respuesta con las unidades apropiadas (como millas por hora, etc.).) es critico. Sin unidades, puede ser difícil para otras personas entender lo que significa su respuesta. También puede perder puntos si olvida escribir la unidad en una tarea escolar.
Método 2 de 3: resolver otros problemas

1. Aislar las diferentes variables para calcular la distancia y el tiempo. Una vez que conozca los conceptos básicos de la ecuación de la velocidad, puede usarla para encontrar algo más que la velocidad. Por ejemplo, si conoce la velocidad y una de las otras variables, puede reorganizar la ecuación para encontrar la información que falta.
- Supongamos que sabemos que un tren ha viajado a una velocidad de 20 kilómetros por hora durante cuatro horas, pero necesitamos saber la distancia que recorrió. En este caso, podemos reordenar la ecuación y resolverla de esta manera:
- velocidad = distancia/tiempo
- velocidad × tiempo = (distancia/tiempo) × tiempo
- velocidad × tiempo = distancia
- 20 km/h × 4 h = distancia = 80 kilómetros

2. Convierta sus unidades si es necesario. A veces puedes calcular la velocidad en una unidad diferente a la que necesitas. En este caso deberías factores de conversión usa para poner tu respuesta en la unidad correcta. Para hacer esto, escribe las relaciones entre tus unidades como una fracción y multiplícalas. Cuando multiplicas, rotas tu fracción según sea necesario para deshacerte de las unidades que no quieres. Esto es mucho más fácil de lo que parece!
- 80 kilómetros × 1 milla/1.6 kilómetros = 50 millas

3. Reemplace la variable `distancia` con fórmulas de distancia si es necesario. Los objetos no siempre viajan en líneas rectas agradables y convenientes. De lo contrario, es posible que no pueda simplemente insertar un valor numérico para la distancia en la ecuación de velocidad estándar. En su lugar, es posible que deba reemplazar la a en s = a/t con una fórmula que modela la distancia que ha viajado el objeto.
- s = (2 × π × r)/t
- s = (2 × π × 10)/0.5
- s = 62.83/0.5 = 125.66 millas/hora

4. Ver que s = a/t a promedio la velocidad da. La ecuación simple y conveniente que usamos para encontrar la velocidad tiene un defecto importante. El valor que da es técnicamente una velocidad media. Esto significa que asume que el objeto que está midiendo tiene la misma velocidad durante todo el recorrido. Como veremos a continuación, puede ser más difícil encontrar la velocidad de un objeto en un momento dado.
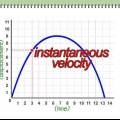
Método 3 de 3: Cálculo de la velocidad instantánea
Observación: Esta sección utiliza técnicas desconocidas para aquellos que no han estudiado cálculo. Consulte nuestros artículos de cálculo para obtener ayuda.

1. Tenga en cuenta que la velocidad se define como la magnitud de la velocidad. Los cálculos de velocidad de nivel más alto pueden ser confusos porque los matemáticos y los científicos usan diferentes definiciones para "velocidad". Una velocidad (velocidad) tiene dos componentes: una magnitud y un dirección. La magnitud es igual a la velocidad del objeto. Un cambio de dirección provocará un cambio en la velocidad (velocidad), pero no en la velocidad.
- Por ejemplo, supongamos que dos automóviles conducen en direcciones opuestas. Los velocímetros de ambos autos marcan 50 km/h, por lo que ambos tienen la misma velocidad. Sin embargo, dado que se separan, podemos decir que un automóvil es un velocidad (velocidad) de -50 km/h y uno tiene un velocidad (velocidad) a partir de 50 km/h.
- Así como puede calcular la velocidad instantánea (rapidez), también puede calcular la calcular la velocidad instantanea (velocidad).

2. Usar valores absolutos para velocidades negativas. Los objetos pueden tener velocidades de magnitud negativa (si se mueven en una dirección negativa en relación con otra cosa). Sin embargo, no existe tal cosa como una velocidad negativa (velocidad), por lo que en estos casos el valor absoluto de magnitud cambia la velocidad del objeto.

3. Tomar la derivada de una función de posición. Si tienes una función s(t) que te da la posición de un objeto con respecto al tiempo, entonces la derivada de s(t) te dará velocidad (velocidad) dar con respecto al tiempo. Simplemente ingrese un valor de tiempo en esta ecuación para la variable t (o cualquiera que sea el valor de tiempo) para obtener la velocidad en este punto. A partir de aquí, encontrar la velocidad es fácil.
- 3t + t - 4
- s`(t) = 2 × 3t + 1
- s`(t) = 6t + 1
- s`(t) = 6(4) + 1 = 24 + 1 = 25 metros/segundo. Esta es técnicamente una medida de velocidad (velocidad), pero dado que es positiva y la dirección no se menciona en el problema, podemos usarla esencialmente para la velocidad.

4. Tomar la integral de una función de aceleración. La aceleración es una forma de cambio en la velocidad de un objeto con el tiempo para medir. Este tema es un poco demasiado complejo para explicarlo completamente en este artículo. Sin embargo, es útil notar que cuando tienes una función a(t) que da aceleración con respecto al tiempo, la integral de a(t) te da velocidad (velocidad) con respecto al tiempo. Tenga en cuenta que es útil conocer la velocidad inicial del objeto para que pueda definir la constante resultante de una integral indefinida.
- a(t) = -30
- v(t)= ∫ a(t)dt =∫ -30dt = -30t + C
- v(0) = 10 = -30(0) + C
- 10 = C, entonces v(t) = -30t + 10
- v(12) = -30(12) + 10 = -360 + 10 = -350. Dado que la velocidad es el valor absoluto de la velocidad, la velocidad del objeto es 350 metros/segundo.
Consejos
- La práctica hace la perfección! Trate de hacer sus propias sumas sustituyendo diferentes números en los problemas de ejemplo anteriores.
- Si está buscando una forma rápida de calcular para cálculos de velocidad avanzados, use aquí que la calculadora de derivadas en línea y la calculadora de integrales en línea aquí.
Artículos sobre el tema. "Calcular velocidad"
Оцените, пожалуйста статью
Popular