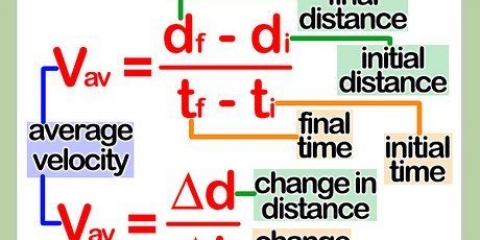
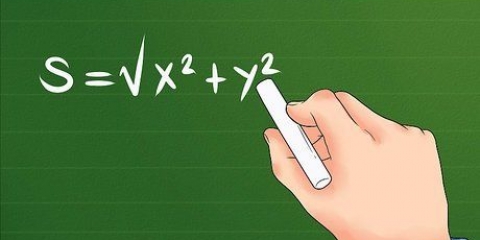Tenga en cuenta, sin embargo, que si las unidades de tiempo utilizadas en su valor de velocidad promedio son diferentes de las de su valor de tiempo, deberá convertir una u otra para que coincidan. Por ejemplo, si una velocidad media se mide en km/h y el tiempo es en minutos, tendrías que dividir el tiempo entre 60 para convertirlo en horas. Resolvamos nuestro problema de muestra. 120 km/h × 0,5 h = 60 kilómetros. Tenga en cuenta que las unidades de tiempo (horas) desprenderse contra las unidades en el denominador de la velocidad promedio (horas), dejando solo las unidades de distancia (km). 
Supongamos que sabemos que un automóvil ha recorrido 60 km en 50 minutos, pero no tenemos valor para la velocidad promedio mientras conduce. En este caso podemos usar la variable sjoya aislar en la ecuación base para la distancia, y obtenemos sjoya = d/t para obtener. Entonces calculamos 60 km/50 minutos = 1,2 km/min. Tenga en cuenta que en nuestro ejemplo, nuestra respuesta para la velocidad tiene una unidad inusual (km/minuto). Para obtener su respuesta en la forma más común de km/hr, multiplíquelo por 60 minutos/hr y obtenga `72 km/h Llegar. 
Ejemplo: En el problema de ejemplo anterior, concluimos que para recorrer 60 km en 50 minutos, tendríamos que viajar a 72 km/h. Sin embargo, esto solo es cierto si viajamos a una velocidad durante todo el viaje. Por ejemplo, si conducimos la mitad del viaje a 80 km/h y la otra mitad a 64 km/h, aún recorremos 60 km en 50 minutos: 72 km/h = 60 km/50 min = ????? Soluciones matemáticas el uso de derivadas suele ser una mejor opción que la fórmula de la distancia para definir la velocidad de un objeto en situaciones reales, porque es probable que haya cambios en la velocidad. 

Tenga en cuenta que esta fórmula utiliza valores absolutos (el símbolo |). Los valores absolutos simplemente significan que los términos dentro de los símbolos se vuelven positivos cuando son negativos. Por ejemplo, digamos que nos detenemos en un tramo de carretera perfectamente recto en el camino. Si hay un pueblo pequeño a 5 km frente a nosotros y una ciudad a 1 km detrás de nosotros, ¿a qué distancia están las dos ciudades?? Si tomamos la ciudad 1 como x1 = considerar 5 y la ciudad 2 como x2 = -1, entonces podemos encontrar d, la distancia entre las dos ciudades, de la siguiente manera: re = |x2 - X1| = |-1 - 5| = |-6| = 6 kilómetros. 
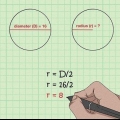
La fórmula de la distancia en el espacio bidimensional utiliza la Teorema de pitágoras, que establece que la hipotenusa de un triángulo rectángulo es igual a la raíz cuadrada de los otros dos lados. Por ejemplo, digamos que tenemos dos puntos en el plano x-y: (3, -10) y (11, 7) que representan respectivamente el centro de un círculo y un punto en el círculo. Para encontrar la distancia recta entre estos dos puntos, podemos resolver lo siguiente: re = √((x2 - X1) + (y2 - y1)) re = √((11 - 3) + (7 - -10)) re = √(64 + 289) re = √(353) = 18.79 
Ejemplo: Digamos que como un astronauta flotando en el espacio cerca de dos asteroides. Uno está a unos 8 km delante de nosotros, 2 km a nuestra derecha y 5 km por debajo de nosotros, mientras que el otro está a 3 km detrás de nosotros, 3 km a nuestra izquierda y 4 km por encima de nosotros. Si representamos las posiciones de estos asteroides con las coordenadas (8.2,-5) y (-3,-3.4), podemos encontrar la distancia entre ambos de la siguiente manera: re = √((-3 - 8) + (-3 - 2) + (4 - -5)) re = √((-11) + (-5) + (9)) re = √(121 + 25 + 81) re = √(227) =15,07 kilometros
Calcular distancia
Contenido
Distancia, a menudo referida como la variable D, es una medida del espacio ocupado por una línea recta entre dos puntos. La distancia puede referirse al espacio entre dos puntos estacionarios (por ejemplo, la altura de una persona es la distancia desde la parte inferior de sus pies hasta la parte superior de su cabeza) o puede referirse al espacio entre la posición actual de un punto en movimiento objeto y su ubicación inicial. La mayoría de los problemas de distancia se pueden resolver con las ecuaciones re = sjoya × t donde d es la distancia, sjoya la velocidad media, y t el tiempo, o la ecuación re = √((x2 - X1) + (y2 - y1)), donde (x1, y1) y (x2, y2) son las coordenadas x e y de dos puntos.
Pasos
Método 1 de 2: determinar la distancia con velocidad y tiempo promedio

1. Determine los valores para la velocidad y el tiempo promedio. Al tratar de encontrar la distancia que ha viajado un objeto en movimiento, dos piezas de información son vitales para hacer este cálculo: el velocidad` (o magnitud de la velocidad) y lahora donde se movió el objeto. Con estos datos, es posible encontrar la distancia recorrida por el objeto, utilizando la fórmula d = sjoya × t.
- Para comprender mejor la aplicación de la fórmula de la distancia, en esta sección vamos a resolver un problema de ejemplo. Digamos que vamos a unos 120 km/h y queremos saber qué distancia recorreremos en media hora. De 120 km/h como nuestro valor para la velocidad media y 0,5 horas como nuestro valor por tiempo, resolveremos este problema en el siguiente paso.

2. Multiplique la velocidad promedio por el tiempo. Una vez que conoce la velocidad promedio de un objeto en movimiento y el tiempo que tardó en moverse, encontrar la distancia que ha recorrido es relativamente fácil. Simplemente multiplique estos dos valores para obtener su respuesta.

3. Edite la ecuación para resolver las otras variables. La simplicidad de la ecuación básica de la distancia (d = sjoya × t) hace que sea bastante fácil usar la ecuación para encontrar los valores de las variables además de la distancia. Aísle la variable que desea resolver de acuerdo con las reglas básicas de matemáticas, y luego ingrese los valores de las otras dos variables, para encontrar el valor de la tercera. En otras palabras, para encontrar la velocidad promedio de su objeto, use la ecuación sjoya = d/t y para encontrar el tiempo que ha viajado un objeto, use la ecuación t = d/sjoya.

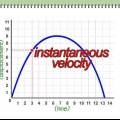
4. Tenga en cuenta que la variablejoya` en la fórmula de distancia se refiere a promedio velocidad. Es importante comprender que la fórmula de distancia estándar proporciona una imagen simplificada del movimiento de un objeto. La fórmula de la distancia supone que el objeto en movimiento tiene una velocidad constante tiene, en otras palabras, asume que el objeto en movimiento se mueve a una velocidad `uniforme` e invariable. Para problemas matemáticos abstractos, como los que se encuentran en un entorno académico, a veces todavía es posible modelar el movimiento de un objeto utilizando esta suposición. Sin embargo, en la vida real, este modelo a menudo no representa con precisión el movimiento de los objetos en movimiento, que en realidad pueden acelerar, desacelerar, detenerse e invertirse con el tiempo.
Método 2 de 2: determinar la distancia entre dos puntos

1. Determinación de dos puntos en un espacio plano. ¿Qué pasa si en lugar de determinar la distancia que ha viajado un objeto en movimiento, necesita determinar la distancia entre dos objetos estacionarios?? En casos como este, la fórmula de distancia basada en la velocidad descrita anteriormente no será de ninguna utilidad. Afortunadamente, existe otra fórmula de distancia para encontrar rápidamente la distancia más corta entre dos puntos. Sin embargo, para esta fórmula necesitas saber las coordenadas de los dos puntos. Si estás tratando con una distancia unidimensional (como en una recta numérica), tus coordenadas son dos números, x1 yx2. Si está tratando con la distancia en dos dimensiones, entonces necesita valores para dos puntos (x, y), (x1,y1) y (x2,y2). Finalmente, para tres dimensiones necesitas valores para (x1,y1,z1) y (x2,y2,z2).

2. Determinar la distancia en una línea restando el valor de las coordenadas de los dos puntos. Calcular la distancia unidimensional entre dos puntos si conoce el valor de cada punto es fácil. Solo usa la fórmula re = |x2 - X1|. En esta fórmula se resta x1 fuera de x2 y tome el valor absoluto de su respuesta para encontrar la distancia entre x1 yx2 encontrar. Normalmente se usa la fórmula de la distancia unidimensional cuando los dos puntos se encuentran en una recta numérica o en un eje.

3. Encuentra la distancia en el plano usando el teorema de Pitágoras. Encontrar la distancia entre dos puntos en un espacio bidimensional es más complicado que en una dimensión, pero no es difícil. Solo usa la fórmula re = √((x2 - X1) + (y2 - y1)). En esta fórmula, resta las dos coordenadas x, eleva al cuadrado el resultado, resta las coordenadas y, eleva al cuadrado el resultado, suma los dos resultados intermedios y calcula la raíz cuadrada para encontrar la distancia entre los dos puntos para encontrar. Esta fórmula funciona en el plano bidimensional, por ejemplo, en los gráficos x/y estándar.

4. Determine la distancia tridimensional cambiando la fórmula del área. En tres dimensiones, los puntos también tienen una coordenada z además de la coordenada x e y. Para encontrar la distancia entre dos puntos en el espacio tridimensional, use re = √((x2 - X1) + (y2 - y1) + (z2 - z1)). Esta es una forma modificada de la fórmula de distancia bidimensional descrita anteriormente que también tiene en cuenta las coordenadas z. Al restar las dos coordenadas z entre sí, elevarlas al cuadrado y ejecutar el resto de la fórmula como se describe anteriormente, estará seguro de que su respuesta final refleja la distancia tridimensional entre los dos puntos.
Artículos sobre el tema. "Calcular distancia"
Оцените, пожалуйста статью
Popular