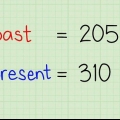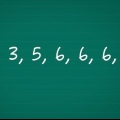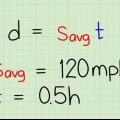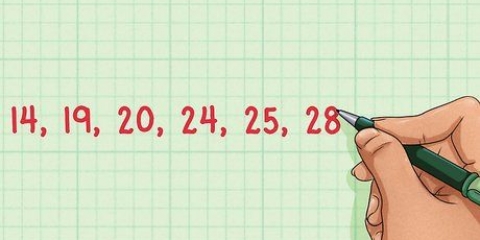Calcular covarianza

Contenido

Pasos
Advertencias

La covarianza es un cálculo estadístico para hacer que la relación entre dos conjuntos de datos sea más transparente. Supongamos, por ejemplo, que los antropólogos estudian la altura y el peso de una población dentro de una cultura particular. Para cada persona en el estudio, la altura y el peso se pueden representar con un par de datos (x, y). Estos valores se pueden utilizar en una fórmula estándar para calcular la relación de covarianza. Este artículo primero explica los cálculos para determinar la covarianza de un conjunto de datos. A continuación, se discutirán otras dos formas automatizadas de determinar el resultado.

Pasos

Método 1 de 4: Calcular la covarianza a mano usando la fórmula estándar

Imagen titulada Calcular covarianza Paso 1

1. Aprenda la fórmula de covarianza estándar y sus partes. La fórmula estándar para calcular la covarianza es

Σ (X I - X_{promedio}) (y_{I} - y_{promedio}) / (norte - 1)

$Sigma (x_{i}-x_{{text{promedio}}})(y_{i}-y_{{text{promedio}}})/(n-1)$ . Para usar esta fórmula, necesita saber el significado de las variables y símbolos:

$Σ$ $Sigma$ - Este símbolo es la letra griega `sigma`. En funciones matemáticas, esto significa agregar una serie de lo que sigue. En esta fórmula, el signo Σ significa que calculas los valores en el numerador de la fracción, luego los sumas todos juntos, luego divides el total por el denominador.
$X I$ $x_{yo}$ - Puedes leer esta variable como `x sub i`. El subíndice i representa un contador. Significa que vas a hacer un cálculo para cada valor de x en tu conjunto de datos.
$X a v gramo$ $x_{{promedio}}$ - El `avg` indica que x(avg) es el valor medio de todos los puntos de datos x. La media a veces se escribe como una x con una línea horizontal corta encima. En ese estilo, lees la variable como `x-barra`, pero aún significa la media del conjunto de datos.
$y I$ $y_{yo}$ - Puedes leer esta variable como `y sub i`. El subíndice i es el numerador. Significa que vas a hacer un cálculo para cada valor de y en tu conjunto de datos.
$y a v gramo$ $y_{{promedio}}$ - El `avg` indica que y(avg) es el valor medio de todos los puntos de datos x. La media a veces se escribe como una y con una línea horizontal corta encima. En ese estilo, lee la variable como `y-barra`, pero aún significa la media del conjunto de datos.
$norte$ $norte$ - Esta variable es el número de elementos en su conjunto de datos. Recuerde que en un problema de covarianza, un solo `elemento` se compone de un valor de x y un valor de y. El valor `n` es el número de pares de puntos de datos, no números individuales.

Imagen titulada Calcular covarianza Paso 2

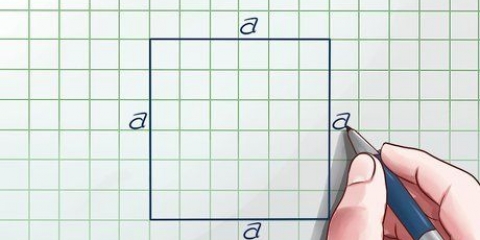
2. Construya su tabla de datos. Antes de comenzar, es útil recopilar sus datos. Crear una tabla con cinco columnas. Debe declarar cada columna de la siguiente manera:

X

$X$ - Rellena esta columna con los valores de los puntos de los datos x.

y

$y$ - Rellena esta columna con los valores de los datos y. Asegúrese de que los valores de y estén alineados con los valores de x correspondientes. En un problema de covarianza, el orden de los puntos de datos y el acoplamiento de x e y son importantes.

(X I - X_{promedio})

$(x_{i}-x_{{text{promedio}}})$ - Deje esta columna en blanco al principio. Vas a llenarlo con datos después de haber promediado los datos x.

(y I - y_{promedio})

$(y_{i}-y_{{texto{promedio}}})$ - Deje esta columna vacía al principio. Vas a llenarlo con datos después de haber promediado los datos y.

Producto

${text{Producto}}$ - Deje la última columna vacía también. Esto se llenará durante el procesamiento de la asignación.

Imagen titulada Calcular covarianza Paso 3

3. Calcule la media de los puntos de datos x. Esta colección de datos de muestra contiene 9 números. Para encontrar el promedio, súmalos y divide la suma por 9. Esto da el resultado 1 + 3 + 2 + 5 + 8 + 7 + 12 + 2 + 4 = 44. Cuando divides esto por 9 obtienes la media 4.89. Este es el valor que usará como x (promedio) para los próximos cálculos.

Imagen titulada Calculate Covariance Step 4

4. Calcule la media de los puntos de datos y. Esta columna y también debe constar de 9 puntos de datos que coincidan con los puntos de datos x. Determine el promedio de este. Para este conjunto de datos de muestra, se convierte en 8 + 6 + 9 + 4 + 3 + 3 + 2 + 7 + 7 = 49. Divida este total por 9 para obtener un promedio de 5.44. Vas a usar 5.44 como el valor de y(avg) para los próximos cálculos.

Imagen titulada Calcular covarianza Paso 5

5. Calcular los valores (XI-Xpromedio){displaystyle (x_{i}-x_{text{promedio}})} $(x_{i}-x_{{text{promedio}}})$ . Para cada elemento en la columna x, calcule la diferencia entre ese número y el valor medio. Para este problema de ejemplo, esto significa restar 4.89 de cada valor de x. Si el punto de datos original es menor que la media, su resultado será negativo. Si el punto de datos original es mayor que la media, entonces el resultado será positivo. Asegúrese de realizar un seguimiento de qué valores son negativos.

Por ejemplo, el primer punto de datos en la columna x es 1. El valor a ingresar en la primera línea de la columna

(X I - X_{promedio})

$(x_{i}-x_{{text{promedio}}})$ es: 1 – 4,89 = -3,89.

Repita este proceso para cada punto de datos. Entonces la segunda línea se convierte en: 3 - 4.89 = -1.89. La tercera línea se convierte en: 2 - 4,89 = -2,89. Continúe este proceso para todos los puntos de datos. Los nueve números de esta columna se convierten en: -3,89, -1,89, -2,89, 0,11, 3,11, 2,11, 7,11, -2,89, -0,89.

Imagen titulada Calculate Covariance Step 6

6. Calcular los valores (yI-ypromedio){displaystyle (y_{i}-y_{text{promedio}})} $(y_{i}-y_{{texto{promedio}}})$ . En esta columna, vas a hacer restas similares, usando los puntos de datos y y la media de y. Si el punto de datos original es menor que la media, el resultado será negativo. Si el punto de datos original es mayor que la media, entonces su resultado será positivo. Asegúrese de realizar un seguimiento de qué valores son negativos.

Entonces, para la primera línea, su cálculo será: 8 -5.44, = 2.56.

La segunda línea se convierte en: 6 – 5,44 = 0,56.

Sigue restando los valores hasta el final de la lista de datos. Cuando haya terminado, debería tener los siguientes nueve valores en esta columna: 2,56, 0,56, 3,56, -1,44, -2,44, -2,44, -3,44, 1,56, 1,56.

Imagen titulada Calcular covarianza Paso 7

7. Calcular los productos para cada fila de datos. Completas las filas de la última columna multiplicando los números que calculaste en las dos columnas anteriores de

(X I - X_{promedio})

$(x_{i}-x_{{text{promedio}}})$ y

(y I - y_{promedio})

$(y_{i}-y_{{texto{promedio}}})$ . Trabaje fila por fila, multiplicando los dos números por sus puntos de datos correspondientes. Cuidado con cualquier valor negativo en el camino.

En la primera fila de estos datos de muestra, el

(X I - X_{promedio})

$(x_{i}-x_{{text{promedio}}})$ usted calculó -3.89, y el

(y I - y_{promedio})

$(y_{i}-y_{{texto{promedio}}})$ valor 2.56. El producto de estos dos números es: -3,89 x 2,56 = -9,96.

Para la segunda fila, multiplica los dos números: -1,88 x 0,56 = -1,06.

Siga multiplicando fila por fila hasta el final del conjunto de datos. Cuando haya terminado, los nueve valores de esta columna deberían ser: -9,96, -1,06, -10,29, -0,16, -7,59, -5,15, -24,46, -4,51, -1,39.

Imagen titulada Calcular covarianza Paso 8

8. Encuentra la suma de los valores en la última columna. Aquí es donde entra el símbolo Σ. Después de hacer todos los cálculos hasta ahora, sume los resultados. Para este conjunto de datos de muestra, ahora debería tener nueve valores en la última columna. Suma esos nueve números juntos. Preste mucha atención a si un número es positivo o negativo.

La suma de este conjunto de datos de muestra debe sumar -64,57. Escriba este total en el espacio en la parte inferior de la columna. Este es el valor del numerador de la fórmula de covarianza estándar.

Imagen titulada Calcular covarianza Paso 9

9. Calcular el denominador de la fórmula de covarianza. El numerador de la fórmula de covarianza estándar es el valor que acaba de calcular. El denominador está representado por (n-1), y es uno menos que el número de pares de datos en su conjunto de datos.

En este problema de ejemplo, hay nueve pares de datos, por lo que n es 9. Por tanto, el valor de (n-1) es igual a 8.

Imagen titulada Calculate Covariance Step 10

10. Divide el numerador entre el denominador. El último paso para calcular la covarianza es dividir el numerador,

Σ (X I - X_{promedio}) (y_{I} - y_{promedio})

$Sigma (x_{i}-x_{{text{promedio}}})(y_{i}-y_{{text{promedio}}})$ por el denominador,

(norte - 1)

$(n-1)$ . El cociente es la covarianza de tus datos.

Para este conjunto de datos de muestra, este cálculo es: -64,57/8 = -8,07.

Método 2 de 4: calcular la covarianza con una hoja de cálculo de Excel

Imagen titulada Calculate Covariance Step 11

1. Observe cuáles son los cálculos repetitivos. La covarianza es un cálculo que tienes que hacer a mano varias veces para que entiendas el significado del resultado. Sin embargo, si va a utilizar la covarianza de forma rutinaria para interpretar los datos, entonces necesita una forma más rápida y automatizada de obtener los resultados. Es posible que ya haya notado que con nuestro conjunto de datos relativamente pequeño de solo nueve pares de datos, los cálculos consistieron en dos promedios, dieciocho restas separadas, nueve multiplicaciones, una suma y finalmente otra división. Son 31 cálculos relativamente pequeños para encontrar la solución. En el camino, corre el riesgo de perder signos negativos o copiar los resultados incorrectamente, lo que hace que la respuesta sea incorrecta.

Imagen titulada Calculate Covariance Step 12

2. Crear una hoja de trabajo para calcular la covarianza. Si está familiarizado con Excel (o cualquier otro programa de cálculo), puede crear fácilmente una tabla para determinar la covarianza. Etiquete los encabezados de las cinco columnas como en los cálculos manuales: x, y, (x(i)-x(promedio)), (y(i)-y(promedio)) y Producto.

Para simplificar la denominación, nombra la tercera columna como "diferencia x" y la cuarta columna "diferencia y", siempre que recuerdes el significado de los datos.

Si la tabla comienza en la esquina superior izquierda de la hoja de trabajo, la celda A1 se etiquetará como x, mientras que las demás etiquetas continuarán hasta la celda E1.

Imagen titulada Calculate Covariance Step 13

3. Rellene los puntos de datos. Escriba los valores de los datos en las dos columnas x e y. Recuerda que el orden de los puntos de datos es importante, por lo que debes unir cada y con el valor correspondiente de x.

Los valores de x comienzan en la celda A2 y continúan hasta la cantidad de puntos de datos que necesita.

Los valores y comienzan en la celda B2 y continúan hasta la cantidad de puntos de datos que necesita.

Imagen titulada Calculate Covariance Step 14

4. Determine las medias de los valores de x e y. Excel calcula los promedios para usted muy rápidamente. En la primera celda en blanco debajo de cada columna de datos, escriba la fórmula =PROMEDIO(A2:A___). Complete el espacio en blanco con el número de la celda que corresponde a su último punto de datos.

Por ejemplo, si tiene 100 puntos de datos, las celdas A2 a A101 se llenarán, por lo que en la celda debe escribir: = PROMEDIO (A2: A101).

Para los datos y, escriba la fórmula = PROMEDIO (B2: B101).

Recuerde que una fórmula en Excel comienza con un signo `=`.

Imagen titulada Calculate Covariance Step 15

5. Escriba la fórmula para la columna (x(i)-x(avg)). En la celda C2, ingrese la fórmula para calcular la primera resta. Esta fórmula se convierte en: =A2-___. Rellene el espacio vacío con la dirección de la celda que contiene el promedio de los datos x.

Por ejemplo, los 100 puntos de datos se promedian en la celda A103, por lo que su fórmula se convierte en: =A2-A103.

Imagen titulada Calculate Covariance Step 16

6. Repita la fórmula para los puntos de datos (y(i)-y(avg)). Siguiendo el mismo ejemplo estará en la celda D2. La fórmula se convierte en: =B2-B103.

Imagen titulada Calculate Covariance Step 17

7. Escriba la fórmula para la columna `Producto`. En la quinta columna debe escribir en la celda E2 la fórmula para calcular el producto de las dos celdas anteriores. Esto entonces se convierte en: =C2*D2.

Imagen titulada Calculate Covariance Step 18

8. Copie las fórmulas para llenar la tabla. Hasta ahora solo ha programado los primeros puntos de datos en la fila 2. Usando su mouse, resalte las celdas C2, D2 y E2. Coloque el cursor en el cuadro pequeño en la esquina inferior derecha hasta que aparezca un signo más. Haga clic y mantenga presionado el botón del mouse y arrastre el mouse hacia abajo para expandir la selección y llenar toda la tabla de datos. Este paso copiará automáticamente las tres fórmulas de las celdas C2, D2 y E2 a toda la tabla. La tabla debe llenarse automáticamente con todos los cálculos.

Imagen titulada Calculate Covariance Step 19

9. Programa la suma de la última columna. Necesita la suma de los artículos en la columna `Producto`. En la celda en blanco inmediatamente debajo del último punto de datos de esa columna, escriba la fórmula: =SUMA(E2:E___). Complete el espacio en blanco con la dirección de la celda del último punto de datos.

En el ejemplo con 100 puntos de datos, esta fórmula va a la celda E103. Tipo: =SUMA(E2:E102).

Imagen titulada Calculate Covariance Step 20

10. Determinar la covarianza. También puede dejar que Excel haga el cálculo final por usted. El último cálculo en la celda E103 en nuestro ejemplo representa el numerador de la fórmula de covarianza. Inmediatamente debajo de esa celda, escriba la fórmula: =E103/___. Complete el espacio en blanco con la cantidad de puntos de datos que tiene. En nuestro ejemplo esto es 100. El resultado es la covarianza de sus datos.

Método 3 de 4: usar calculadoras de covarianza en línea

Imagen titulada Calculate Covariance Step 21

1. Busque en línea calculadoras de covarianza. Varias escuelas, empresas u otras fuentes tienen sitios web que calculan los valores de covarianza muy fácilmente para usted. Use el término de búsqueda `calculadora de covarianza` en un motor de búsqueda.

Imagen titulada Calculate Covariance Step 22

2. Introduce tus detalles. Lea atentamente las instrucciones en el sitio web para asegurarse de ingresar la información correctamente. Es importante que sus pares de datos se mantengan en orden, de lo contrario, el resultado generado será una covarianza incorrecta. Los sitios web tienen diferentes estilos de entrada de datos.

En el sitio web http://ncalculadoras.com/statistics/covariance-calculator.htm, por ejemplo, hay un cuadro horizontal para ingresar los valores x y un segundo cuadro horizontal para ingresar los valores y. Debes ingresar tus datos separados por comas. Entonces, el conjunto de datos x calculado anteriormente en este artículo debe ingresarse como 1,3,2,5,8,7,12,2,4. Los datos y como 8,6,9,4,3,3,2,7,7.

en otro sitio, https://www.la calculadora.co/math/Covariance-Calculator-705.html, se le pedirá que ingrese los datos x en el primer cuadro. Los datos se ingresan verticalmente, con un elemento por línea. Por lo tanto, la entrada en este sitio se ve así:

Imagen titulada Calculate Covariance Step 23

3. Calcula tus resultados. Lo atractivo de estos cálculos en línea es que luego de ingresar los datos generalmente solo debes hacer clic en el botón `Calcular`, luego de lo cual los resultados aparecen automáticamente. La mayoría de los sitios le proporcionarán los cálculos intermedios de x(avg), y(avg) y n.

Método 4 de 4: Interpretar los resultados de la covarianza

Imagen titulada Calculate Covariance Step 24

1. Busca una relación positiva o negativa. La covarianza es un número estadístico único que indica la relación entre un conjunto de datos y otro. En el ejemplo mencionado en la introducción, la altura y el peso se miden. Se esperaría que a medida que las personas crecen, su peso también aumentará, lo que lleva a una visión de covarianza positiva. Otro ejemplo: supongamos que se recopilan datos que indican la cantidad de horas que una persona ha estado practicando golf y el puntaje que logra. En este caso, espera una covarianza negativa, lo que significa que a medida que aumenta la cantidad de horas de entrenamiento, la puntuación de golf disminuirá. (En golf, cuanto más bajo es mejor).

Considere el conjunto de datos de muestra calculado anteriormente. La covarianza resultante es -8.07. El signo menos significa que a medida que aumentan los valores de x, los valores de y tienden a disminuir. Puede ver que esto es cierto al observar algunos de los valores. Por ejemplo, los valores x de 1 y 2 corresponden a los valores y de 7, 8 y 9. Los valores de x de 8 y 12 están vinculados a los valores de y de 3 y 2 respectivamente.

Imagen titulada Calculate Covariance Step 25

2. Interpretar el tamaño de la covarianza. Si el número de la puntuación de covarianza es grande, ya sea un número positivo grande o un número negativo grande, entonces puede interpretar esto como dos elementos de datos que están fuertemente conectados, ya sea de forma positiva o negativa.

La covarianza -8.07 del conjunto de datos de muestra es bastante grande. Tenga en cuenta que los datos van del 1 al 12. Entonces 8 es un número bastante grande. Esto indica una relación bastante fuerte entre los conjuntos de datos x e y.

Imagen titulada Calculate Covariance Step 26

3. Comprender la falta de una relación. Si su resultado es una covarianza igual o muy cercana a 0, entonces puede concluir que los puntos de datos no tienen relación. Es decir, un aumento en un valor puede, pero no necesariamente, conducir a un aumento en el otro. Los dos términos están vinculados casi arbitrariamente.

Suponga que relaciona las tallas de zapatos con las calificaciones de los exámenes. Debido a que hay tantos factores que afectan las calificaciones de los exámenes de un estudiante, se espera una puntuación de covarianza cercana a 0. Esto indica que casi no hay relación entre los dos valores.

Imagen titulada Calculate Covariance Step 27

4. Ver la relación gráficamente. Para comprender la covarianza visualmente, puede trazar sus puntos de datos en un gráfico x, y. Cuando haga eso, debería ver fácilmente que los puntos, aunque no están exactamente en línea recta, tienden a acercarse a un grupo en una línea diagonal de arriba a la izquierda a abajo a la derecha. Esta es la descripción de una covarianza negativa. También ves que el valor de la covarianza es -8.07. Este es un número bastante grande en comparación con los puntos de datos. El número alto sugiere que la covarianza es bastante fuerte, lo que se puede deducir de la forma lineal de los puntos de datos.

Para repasar esto nuevamente, lea los artículos de wikiHow sobre cómo dibujar puntos en un sistema de coordenadas.

Advertencias

La covarianza tiene una aplicación limitada en estadísticas. A menudo es un paso hacia el cálculo de coeficientes de correlación u otros conceptos. Tenga cuidado con las interpretaciones demasiado audaces basadas en una puntuación de covarianza.