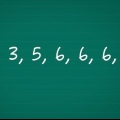Calcular la propagación

El `rango` en la estadística representa la diferencia entre los valores más altos y más bajos en un conjunto de datos. El rango muestra cuán dispersos están los valores en una serie. Si el rango es amplio, entonces los valores de la serie están muy separados; si el rango es pequeño, entonces los valores están cerca uno del otro. Si quieres saber cómo calcular el ancho de esparcimiento, todo lo que necesitas hacer es seguir estos pasos.

Pasos

Consejos

• La mediana de un conjunto de datos estadísticos representa el `medio` del conjunto de datos en términos de distribución y no el rango de los datos. Entonces, si bien es tentador suponer que la mediana de un conjunto de datos determinado es el rango dividido por 2, o la mitad de los extremos del rango, este no suele ser el caso. Para encontrar la mediana correcta, primero debe ordenar los elementos de datos y luego encontrar el elemento en el medio de la lista. ese elemento es la mediana. Por ejemplo, si tiene una lista con 29 elementos, el elemento 15 es equidistante de la parte superior e inferior de la lista ordenada. Entonces, el elemento 15 es la mediana, independientemente de cómo se relacione ese valor con el rango.
• También puede entender `propagación` en un contexto algebraico, donde generalmente se llama `rango`. Para entender esto primero debes hacerte una idea del concepto de función algebraica, o secuencia de operaciones sobre un número dado. Debido a que las operaciones de la función se pueden realizar en cualquier número, incluso en un número desconocido, el número está representado por una variable de letra, generalmente "x". El dominio es el conjunto de todos los valores de entrada posibles que puedes reemplazar con este número desconocido. El alcance de la función es el conjunto de todos los posibles resultados que puedes obtener si ingresas uno de los valores del dominio y realizas todas las operaciones de la función. Desafortunadamente, no hay una sola forma de calcular el rango de una función. A veces, graficar la función o calcular múltiples valores puede mostrar un patrón claro. También puede usar lo que sabe sobre el dominio de la función para excluir posibles valores de salida o para limitar el conjunto de datos que indica el alcance.

Artículos sobre el tema. "Calcular la propagación"

Calcular valores atípicos

Calcular la desviación estándar

Calcular frecuencia acumulada

Calcular varianza