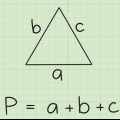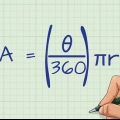Calcular pi

Contenido

Pasos
Consejos

Pi (π) es uno de los números más importantes y fascinantes de las matemáticas. Simplemente se muestra como 3.14, se usa como constante para calcular la circunferencia de un círculo, usando su radio o diámetro. También es un número irracional, lo que significa que puede calcularlo hasta un número infinito de lugares decimales sin encontrar un patrón repetitivo. Esto hace que sea difícil, pero no imposible, trabajar con precisión.

Pasos

Método 1 de 5: Calcular Pi usando un círculo

1. Asegúrate de usar un círculo perfecto. Este método no funcionará con una elipse, elipse o cualquier otra cosa que no sea un círculo real. Un círculo se define como todos los puntos en un plano que son equidistantes de un punto central dado. Por ejemplo, las tapas de un tarro de mermelada son una buena herramienta para este ejercicio. Puede calcular aproximadamente un valor de Pi con esto. Incluso el lápiz más delgado y afilado sigue siendo enorme en comparación con la precisión requerida para un cálculo exacto del número Pi.

2. Mida la circunferencia del círculo con la mayor precisión posible. La circunferencia es la longitud de toda la circunferencia del círculo. Dado que esto está dando vueltas, puede ser un poco complicado de medir (es por eso que Pi es tan importante).

Coloque un hilo alrededor de la circunferencia, con la mayor precisión posible. Marque el cable cuando el círculo esté completo, luego mida la longitud del cable con una regla.

3. Mide el diámetro del círculo. El diámetro es la longitud de la sección transversal de un círculo a través del centro del círculo.

4. Usa la fórmula. La circunferencia de un círculo se puede encontrar con la fórmula C=π*d=2*π*r. entonces pi es igual a la circunferencia del circulo dividida por el diametro. Ingrese sus números en una calculadora: el resultado debe ser alrededor de 3.debería tener 14.

5. Para un resultado más preciso, repita este proceso para varios círculos, luego promedie los resultados. Es posible que sus lecturas no sean perfectas cuando se trata de una lectura individual, pero con el tiempo, el promedio debería ser una muy buena aproximación de Pi.

Método 2 de 5: calcular Pi usando series infinitas

1. Hacer uso de la serie Gregory-Leibniz. Los matemáticos han encontrado varias secuencias matemáticas que, si se siguen hasta el infinito, pueden calcular Pi con una enorme cantidad de decimales. Algunas de estas secuencias son tan complejas que se necesitan supercomputadoras para procesarlas. Sin embargo, una de las más simples es la serie de Gregory-Leibniz. Tal vez no sea muy eficiente, pero produce un número más preciso para pi con cada iteración, y eventualmente termina en 5 decimales después de 500.000 iteraciones. Aquí está la fórmula a utilizar.

π=(4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
Toma 4 y resta 4 dividido por 3 de este. Luego suma 4 dividido por 5. Luego resta 4 dividido por 7 nuevamente. Sigue repitiendo este patrón con un numerador 4 y un número impar consecutivo en el denominador. Cuanto más hagas esto, más te acercarás a pi.

2. Aprovecha las gamas de Nilakantha. Esta es otra serie infinita que te permite calcular pi y no es difícil de entender. Aunque es un poco más complicado, puedes calcular pi mucho más rápido que con la fórmula de Leibniz.

π=3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11 *12) - 4/(12*13*14) ...

Aplicas esta fórmula tomando primero 2 y luego alternativamente sumando y restando fracciones, con el numerador 4 y el denominador el producto de 3 enteros consecutivos que aumentan con cada nueva iteración. Cada fracción consecutiva comienza con una serie de números enteros donde el primer número de la serie es el último número de la serie anterior (en la fracción anterior). Incluso si solo haces esto unas pocas veces, pronto te acercarás a pi.

Método 3 de 5: calcular Pi usando el problema de la aguja de Buffon

1. Prueba el siguiente experimento para calcular pi lanzando perritos calientes. Pi también aparece en el experimento mental llamado Problema de la aguja de Buffon, que trata de determinar la probabilidad de que objetos de forma similar lanzados al azar aterricen entre o sobre una serie de líneas paralelas en el suelo. Resulta que si la distancia entre las líneas es igual a la longitud de los objetos lanzados, entonces la cantidad de veces que los objetos aterrizan en una línea después de muchos lanzamientos se puede usar para calcular pi.

Los científicos y los matemáticos aún no han descubierto una forma de calcular pi exactamente, porque aún no han encontrado un material tan delgado que pueda realizar cálculos exactos con él.

Método 4 de 5: calcular Pi con un límite

1. Elige un número grande. Cuanto mayor sea el número, más preciso será su cálculo.

2. Usa el número, al que llamaremos x, en esta fórmula para calcular pi:x *pecado (180 / x). Para que esto funcione, asegúrese de que su calculadora esté configurada en grados. La razón por la que esto se llama límite es que su resultado está `limitado` a pi. A medida que aumenta su número x, el resultado se acerca más y más al valor de pi.

Método 5 de 5: función arcoseno y seno inverso

1. Elija un número entre -1 y 1. Esto se debe a que el arcoseno no está definido para números mayores que 1 o menores que -1.

2. Use el número en la siguiente fórmula y el resultado es aproximadamente igual a pi.

pi=2 *(Arcsen(raíz cuadrada(1 - x^2))) + abs(Arcsen(x)).

Arcsen se refiere a un seno inverso en radianes

Sqrt es una abreviatura de la raíz cuadrada de

Abs es una abreviatura de valor absoluto

x^2 es una cierta potencia, en este caso x al cuadrado.

Consejos

Calcular pi es divertido y desafiante, pero si calcula demasiados lugares decimales, no será de mucha utilidad .Los astrónomos dicen que no se necesitan más de 39 decimales para que el número pi haga cálculos de alta precisión.