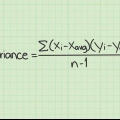Calcular la varianza: 8 pasos (con fotos)

Contenido

Pasos
Consejos

Calcular la varianza le permite medir la dispersión de un conjunto de valores: el grado en que una cantidad de valores difieren entre sí. La varianza es uno de los componentes de la distribución de probabilidad e indica hasta qué punto los valores se desvían de la media. La varianza se usa a menudo junto con la desviación estándar (la raíz cuadrada de la varianza). Si desea saber cómo calcular la varianza de un conjunto de valores, siga los pasos a continuación.

Pasos

1. Escribe la formula para calcular la varianza. La estimación para calcular una estimación aleatoria de la varianza de la población a partir de una muestra fija de n observaciones es la siguiente definición:(s) = Σ [(x_I - x̅)]/n - 1. La fórmula para calcular la varianza en toda una población es la misma que la anterior, excepto que el denominador no es igual a n – 1, sino a n. Siempre que se trate de un conjunto finito de observaciones, es mejor utilizar la primera fórmula. Aquí hay una explicación de las variables de la fórmula:

s = Varianza
Σ = Suma, la suma de todos los términos en la ecuación después del signo de suma.
X_I = Los valores de la muestra.
x̅ = La media de los valores de la serie.
n = El tamaño de la muestra. El número de valores en la serie.

2. Calcular la suma de los valores de la serie. Primero cree una tabla con una columna para los valores, el valor menos la media (x_I - x̅) y luego el cuadrado de estos términos [(x_I - X))]. Una vez que haya terminado con la tabla y rellenado la primera columna, sume todos los valores de la serie. Suponga que está tratando con la siguiente secuencia de números: 17, 15, 23, 7, 9, 13. Sumado esto es: 17 + 15 + 23 + 7 + 9 + 13 = 84.

3. Calcular el promedio. Divide la suma de los números de la serie por el número de elementos de la serie para calcular la media. Así que en este caso la suma 84 dividida por el número de números, 6. 84/6 = 14. escribir "14" en la parte inferior de la columna como un promedio.

4. Resta la media de cada valor de la serie. Reste 14 de cada valor de la serie y complete la tercera columna (la media de la muestra). Puede comprobar su trabajo comprobando si la suma de todos los resultados es cero. Aquí se explica cómo calcular la desviación de la media para cada valor de la serie:

17 - 14 = 3

15 - 14 = 1

23 - 14 = 9

7 - 14 = -7

9 - 14 = -5

13 - 14 = -1

5. Cuadrar cada resultado. Después de calcular la desviación de la media, elévala al cuadrado y escribe la respuesta en la cuarta columna. Entonces todas las respuestas son positivas. Así es como funcionó:

3 = 9

1 = 1

9 = 81

(-7)= 49

(-5) = 25

(-1)= 1

6. Calcular la suma de cuadrados. Sume los resultados juntos. 9 + 1 + 81 + 49 + 25 + 1 = 166

7. Sustituye los valores en la ecuación. Completa los valores en la ecuación. Recuérdalo "norte" representa el número de elementos en la secuencia.

s = 166/(6-1)

8. Resolver. Ahora divide 166 por 5. El resultado es 33.2. Si también quiere saber la desviación estándar, encuentre la raíz cuadrada de 33.2. √33,2 = 5,76. Ahora puede comenzar a interpretar estos datos en relación con el panorama general. Usualmente se compara la varianza de dos series. El valor más bajo significa que en esa serie la varianza es menos grande.