Si la medida experimental es de 60 cm, entonces el cálculo de la imprecisión también deberá redondearse a un número entero. Por ejemplo, la imprecisión de esta medida puede ser de 60 cm ± 2 cm, pero no de 60 cm ± 2.2cm. Si su lectura experimental es igual a 3.4 cm, entonces la imprecisión también tendrá que redondearse a 0,1 cm. Por ejemplo, la imprecisión de esta medida puede ser de 3.4 cm ± .sea de 1 cm, pero no de 3.4 cm ± 1 cm. 
Mire de cerca el borde de la bola y la regla para tener una idea de cuán confiable puede ser su medición. En una regla estándar, las marcas de 0,5 cm están claramente marcadas, pero suponga que puede acercarse un poco más. Si parece que puede obtener una precisión de 0,3 cm con su medida, entonces la inexactitud es de 0,3 cm. Ahora vamos a medir el diámetro de la pelota. Suponga que obtiene 7,6 cm como respuesta. Ahora anote la medida estimada con la inexactitud. El diámetro de la bola es de 7,6 cm ± 0,3 cm. 
Suponga que no puede acercarse mucho más de 0,2 cm con una regla regular. Entonces, la imprecisión es de ± 0,2 cm. Supón que mides que la pila de cajas juntas mide 22 cm. Ahora todo lo que tienes que hacer es dividir este valor de medición y la inexactitud por 10 (el número de cajas). 22 cm/10 = 2,2 cm y 0,2 cm/10 = 0,02 cm. Esto significa que el grosor de 1 caja es igual a 2,20 cm ± 0,02 cm. 



0,43 s – 0,42 s = 0,01 s 0,52 s - 0,42 s = 0,1 s 0,35 s - 0,42 s = -0,07 s 0,29 s - 0,42 s = -0,13 s 0,49 s - 0,42 s = 0,07 s Ahora suma los cuadrados de las diferencias: (0.01 s) + (0.1 s) + (-0.07 s) + (-0.13 s) +(0.07 s)= 0.037 s. Encuentra la media de estos cuadrados sumados dividiendo el resultado por 5. 0,037 s/5 = 0,0074 s. 



(10 cm ± .4 cm) - (3 cm ± .2 cm) = (10 cm - 3 cm) ± (.4cm +. 2 cm) = 7 cm ± 0,6 cm (6 cm ± 0,2 cm) = (0,2 / 6) x 100 y agréguele un signo de %. Eso es 3.3%
Por lo tanto:
(6 cm ± 0,2 cm) x (4 cm ± 0,3 cm) = (6 cm ± 3,3 %) x (4 cm ± 7,5 %) (6 cm x 4 cm) ± (3.3 + 7.5) = 24 cm ± 10,8 % = 24 cm ± 2,6 cm (10 cm ± 0,6 cm) ÷ (5 cm ± 0,2 cm) = (10 cm ± 6%) ÷ (5 cm ± 4%) (10cm ÷ 5cm) ± (6% + 4%) = 2 cm ± 10 % = 2 cm ± 0,2 cm 
(2,0 cm ± 1.0 cm) = (2,0 cm) ± (1,0 cm) x 3 = 8,0 cm ± 3 cm
Calcular imprecisión
Contenido
Cuando toma una medida mientras recopila datos, puede suponer que hay un "valor real" está dentro del rango de las medidas que ha realizado. Si desea calcular la inexactitud de sus lecturas, deberá encontrar la mejor estimación de su lectura y tenerla en cuenta al restar o sumar la inexactitud de la lectura.
Pasos
Método 1 de 3: aprender los conceptos básicos

1. Determinar la forma correcta para la imprecisión. Suponga que mide la longitud de un palo de unos 4,2 cm, con un margen de 1 milímetro. Esto significa que es casi seguro que el palo mide 4,2 cm, pero puede ser un poco más grande o más pequeño que esta longitud, con un margen de error de 1 milímetro.
- Registre esto de la siguiente manera: 4,2 cm ± 0,1 cm. Puedes reescribir esto como: 4,2 cm ± 1 mm, porque 0,1 cm = 1 mm.

2. Redondee la lectura experimental al mismo número de lugares decimales que la inexactitud. Las mediciones que involucran imprecisión generalmente se redondean a 1 o 2 cifras significativas. El punto clave es que redondee las medidas del experimento al mismo número de lugares decimales que la inexactitud, para mantener la coherencia de las medidas.

3. Calcular la imprecisión de una sola medida. Suponga que mide el diámetro de una bola redonda con una regla. Esto es complicado porque es difícil determinar exactamente dónde está el borde exterior de la pelota y cómo medirlo con la regla. Suponga que la regla puede encontrar el diámetro con una precisión de 0,1 cm; esto no significa que pueda medir el diámetro de la pelota con ese nivel de precisión.

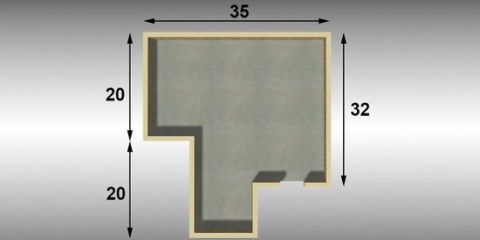
4. Calcule la imprecisión de una sola medición de múltiples objetos. Suponga que mide la altura de una pila de 10 cajas de CD que tienen dimensiones. Supongamos que desea saber cuál es el grosor de 1 caja. Esta lectura es tan pequeña que el porcentaje de imprecisión será alto. Pero si mide 10 cajas, puede dividir el resultado y simplemente dividir su imprecisión por la cantidad de cajas en la pila para encontrar el grosor de 1 caja.

5. Realice esta medición varias veces. Para aumentar la precisión de su medición, ya sea que esté midiendo la longitud de un objeto o la cantidad de tiempo que tomó cubrir una cierta distancia, aumentará las posibilidades de una lectura precisa si toma varias medidas. Determinar el promedio de todas las mediciones resultará en última instancia en una mejor determinación de la inexactitud de una medición.
Método 2 de 3: Cálculo de la imprecisión de múltiples mediciones

1. Tomar varias medidas. Supongamos que desea calcular cuánto tarda una bola en caer de la mesa a la ronda. Para obtener los mejores resultados, deberá realizar la misma medición al menos varias veces; digamos que hacemos esto cinco veces. Luego tendrá que calcular la media de estas 5 medidas y luego sumar o restar la desviación estándar de esto, para obtener el mejor resultado.
- Suponga que tiene las siguientes lecturas: 0,43 s, 0,52 s, 0,35 s, 0,29 s y 0,49 s.

2. Determinar el promedio de las medidas. Lo haces sumando los cinco y dividiendo la suma por 5, el número de valores medidos. 0,43 s + 0,52 s + 0,35 s + 0,29 s + 0,49 s = 2.08 s. Comparte ahora 2.08 por 5. 2.08/5 = 0,42 seg. La media es 0.42 s.

3. Determine la varianza de estas medidas. Esto se hace determinando la diferencia entre cada una de las 5 medidas y el promedio. Restar las lecturas de 0,42 s. Aquí están las 5 diferencias:

4. Determinar la desviación estándar. Esto se puede encontrar calculando la raíz cuadrada de la varianza. El cuadrado de 0,0074 s = 0,09 s, por lo que la desviación estándar es 0,09 s.

5. Dar el valor medido final. Para ello, anote la media de los valores medidos junto con la desviación estándar sumada y restada. Dado que la media de las lecturas es 0,42 s y la desviación estándar es 0,09 s, la lectura final es 0,42 s ± 0,09 s.
Método 3 de 3: operaciones aritméticas con imprecisión

1. Adición de inexactitud. Esto se hace sumando las lecturas y sumando sus imprecisiones:
- (5 cm ± .2 cm) + (3 cm ± .1 cm) =
- (5 cm + 3 cm) ± (.2cm +. 1 cm) =
- 8 cm ± .3cm

2. Restar inexactitud. Esto se hace restando los valores medidos y sumando las imprecisiones:
3. Multiplicar imprecisión.
Para multiplicar la inexactitud, multiplique las medidas y agregue la inexactitud RELATIVA (como porcentaje):
Calcular imprecisiones a través de la multiplicación no funciona con valores absolutos (como con la suma y la resta), pero sí con valores relativos. La inexactitud relativa se obtiene dividiendo la inexactitud absoluta por el valor medido y luego multiplicándola por 100.
Por ejemplo:
Para multiplicar la inexactitud, multiplique las medidas y agregue la inexactitud RELATIVA (como porcentaje):
Calcular imprecisiones a través de la multiplicación no funciona con valores absolutos (como con la suma y la resta), pero sí con valores relativos. La inexactitud relativa se obtiene dividiendo la inexactitud absoluta por el valor medido y luego multiplicándola por 100.
Por ejemplo:
Por lo tanto:
4. Compartir inexactitud.
Para dividir la imprecisión, divida las medidas y agregue la imprecisión RELATIVA:
Este procedimiento es equivalente a una multiplicación!
Para dividir la imprecisión, divida las medidas y agregue la imprecisión RELATIVA:
Este procedimiento es equivalente a una multiplicación!

5. Aumentar una lectura inexacta exponencialmente. Para aumentar exponencialmente una medida inexacta, aumente la medida en una cierta potencia, luego multiplique la inexactitud por esa potencia:
Consejos
- Puede ver los resultados y la imprecisión predeterminada como un todo, o para cada resultado dentro de un conjunto de datos. Una regla general es que los datos obtenidos de múltiples mediciones son menos precisos que los obtenidos directamente de una medición individual.
Advertencias
- La imprecisión que se describe aquí solo se aplica a aquellos casos en los que se utilizan estadísticas normales (gaussianas, en forma de campana). Otros diferenciales requieren un método diferente para describir la inexactitud.
- La buena investigación nunca termina "hechos" o que "cierto" es. Si bien es muy probable que una medición caiga dentro de un cierto rango de inexactitud, no hay garantía de que lo hará. Es inherente a los valores medidos científicos que existe la posibilidad de que los valores medidos sean incorrectos.
Artículos sobre el tema. "Calcular imprecisión"
Оцените, пожалуйста статью
Popular