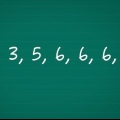Sigamos trabajando con el ejemplo anterior. Aquí está nuestro conjunto de datos que muestra las temperaturas en grados Fahrenheit de varios objetos en una habitación: {71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}. Si ordenamos los valores del conjunto de menor a mayor, este se convierte en nuestro nuevo conjunto: {69, 69, 70, 70, 70, 70, 71, 71, 71, 72, 73, 300}. 
No se deje confundir por conjuntos de datos con un número par de puntos: el promedio de los dos puntos medios suele ser un número que no está en el conjunto de datos en sí; está bien. Sin embargo, si los dos puntos medios son iguales, la media, por supuesto, también será este número; esto también es Okey. En nuestro ejemplo tenemos 12 puntos. Los dos términos del medio son los puntos 6 y 7 – 70 y 71. respectivamente. Entonces, la mediana de nuestro conjunto de datos es la media de estos dos puntos: ((70 + 71) / 2)=70.5. 
En nuestro ejemplo, seis puntos están por encima de la mediana y seis por debajo. Entonces, para encontrar el primer cuartil, debemos tomar el promedio de los dos puntos medios en los seis puntos inferiores. Los puntos 3 y 4 de los seis inferiores son ambos 70, por lo que su media es ((70 + 70) / 2)=70. Entonces nuestro valor para Q1 es 70. 
Siguiendo con el ejemplo anterior, vemos que los dos puntos medios de los seis puntos por encima de la mediana son 71 y 72. La media de estos dos puntos es ((71 + 72) / 2)=71.5. Entonces nuestro valor para Q3 es 71.5. 
En nuestro ejemplo, los valores para Q1 y Q3 son 70 y 71,5 respectivamente. Para encontrar el rango intercuartil, calculamos Q3 - Q1: 71.5 - 70=1,5. Esto funciona incluso si Q1, Q3 o ambos números son negativos. Por ejemplo, si nuestro valor para Q1 fuera -70, el rango intercuartílico sería 71,5 - (-70)=141,5, lo cual es correcto. 
En nuestro ejemplo, el rango intercuartílico es (71.5 - 70), o 1.5. Multiplica esto por 1.5 y obtienes 2.25. Agregamos este número a Q3 y lo restamos de Q1, para encontrar los límites internos de la siguiente manera: 71,5 + 2,25 = 73,75 70 - 2,25=67,75 Así que las fronteras internas son 67,75 y 73,75. En nuestro conjunto de datos, solo la temperatura del horno, 300 grados Fahrenheit, está fuera de este rango. Así que esto puede ser un valor atípico leve. Sin embargo, todavía tenemos que determinar si esta temperatura es un valor atípico extremo, así que no saquemos conclusiones precipitadas todavía.

En nuestro ejemplo, multiplicamos el rango intercuartílico por 3 y llegamos a (1.5 *3) o 4.5. Ahora podemos encontrar los límites exteriores de la misma manera que los límites interiores: 71,5 + 4,5=76 70 - 4,5=65,5 Entonces los límites exteriores son 65.5 y 76. Los puntos de datos que están fuera de las fronteras exteriores se consideran valores atípicos extremos. En nuestro ejemplo, la temperatura del horno, 300 grados Fahrenheit, está muy por fuera de los límites exteriores. Entonces la temperatura del horno es seguro un caso atípico extremo.

Otro criterio a considerar es si los valores atípicos afectan la media de un conjunto de datos de una manera sesgada o engañosa. Esto es especialmente importante si tiene la intención de sacar conclusiones del promedio de su conjunto de datos. Revisemos nuestro ejemplo. Desde que altamente Si bien es poco probable que el horno alcanzara una temperatura de 300 °F debido a alguna fuerza imprevista de la naturaleza, en nuestro ejemplo podemos concluir con casi un 100 % de certeza que el horno se dejó encendido accidentalmente, lo que resultó en una lectura de temperatura anormalmente alta. Además, si no eliminamos el valor atípico, nuestro conjunto de datos promedia (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73 + 300)/12 = 89,67 °F, mientras que el promedio sin que el valor atípico sale en (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73)/11=70,55 °F. Dado que el valor atípico fue causado por un error humano, y dado que es incorrecto decir que la temperatura ambiente promedio estuvo cerca de los 32 °C, debemos elegir elegir nuestro valor atípico retirar. 
Por ejemplo, imagina que estamos diseñando un nuevo fármaco para que los peces crezcan más en una piscifactoría. Usemos nuestro antiguo conjunto de datos ({71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}), excepto que ahora cada punto representa la masa de un pez (en gramos) después tratamiento con otro fármaco experimental desde el nacimiento. En otras palabras, la primera droga le dio a un pez una masa de 71 gramos, la segunda le dio a otro pez una masa de 70 gramos, y así sucesivamente. En esta situación 300. es aún un gran valor atípico, pero no deberíamos eliminarlo ahora. Porque, si asumimos que el valor atípico no es el resultado de un error, representa un gran éxito en nuestro experimento. La droga que produjo un pez de 300 gramos funcionó mejor que cualquier otra droga, así que esto es todo más importante punto de datos en nuestro conjunto, en lugar de la menos punto de datos importante.
Calcular valores atípicos
Contenido
A parte aislada o parte aislada en estadística, un punto de datos que difiere significativamente de los otros puntos de datos en una muestra. A menudo, los valores atípicos señalan a los estadísticos anomalías o errores en las mediciones, después de lo cual pueden eliminar el valor atípico del conjunto de datos. Si realmente eligen eliminar los valores atípicos del conjunto de datos, eso podría generar cambios significativos en las conclusiones extraídas del estudio. Por eso es importante calcular y determinar los valores atípicos si desea interpretar correctamente los datos estadísticos.
Pasos

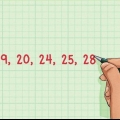
1. Aprenda a detectar posibles valores atípicos. Antes de que podamos decidir si eliminar los valores anómalos de un conjunto de datos en particular, debemos, por supuesto, reconocer los posibles valores atípicos en el conjunto de datos. En general, los valores atípicos son los puntos de datos que se desvían significativamente de la tendencia de los otros valores en el formulario establecido; en otras palabras, ellos salir de los otros valores. Por lo general, es fácil reconocer esto en tablas y (especialmente) en gráficos. Si el conjunto de datos se grafica visualmente, los valores atípicos estarán `lejos` de los otros valores. Por ejemplo, si la mayoría de los puntos en un conjunto de datos forman una línea recta, los valores atípicos no se ajustarán a esta línea.
- Veamos un conjunto de datos que muestra las temperaturas de 12 objetos diferentes en una habitación. Si la temperatura de 11 de los objetos fluctúa alrededor de 21 °C en unos pocos grados como máximo, mientras que un objeto, un horno, tiene una temperatura de 150 °C, puede ver de un vistazo que el horno es probablemente un valor atípico.

2. Ordenar todos los puntos de datos de menor a mayor. El primer paso para calcular valores atípicos es encontrar el valor mediano (o el valor medio) del conjunto de datos. Esta tarea se vuelve mucho más fácil si los valores en el conjunto están ordenados de menor a mayor. Entonces, antes de continuar, ordene los valores en su conjunto de datos de esta manera.

3. Calcular la mediana del conjunto de datos. La mediana de un conjunto de datos es el punto de datos donde la mitad de los datos está por encima y la mitad de los datos está por debajo; es básicamente el "centro" del conjunto de datos. Si el conjunto de datos contiene un número impar de puntos, la mediana es fácil de encontrar: la mediana es el punto con tantos puntos por encima como por debajo. Si hay un número par de puntos, como no hay un punto medio, debes sacar el promedio de los dos puntos medios para encontrar la mediana. Al calcular valores atípicos, la mediana generalmente se denota con la variable Q2, porque se encuentra entre Q1 y Q3, el primer y tercer cuartil. Determinaremos estas variables más adelante.

4. Calcular el primer cuartil. Este punto, al que nos referimos como la variable Q1, es el punto de datos por debajo del cual se encuentra el 25 por ciento (o una cuarta parte) de las observaciones. En otras palabras, este es el punto medio de todos los puntos en su conjunto de datos debajo la mediana. Si hay un número par de valores por debajo de la mediana, debe volver a promediar los dos valores medios para encontrar Q1, como puede que ya haya hecho para determinar la mediana usted mismo.

5. Calcular el tercer cuartil. Este punto, que denotamos con la variable Q3, es el punto de datos por encima del cual se encuentra el 25 por ciento de los datos. Encontrar Q3 es prácticamente lo mismo que encontrar Q1, excepto que en este caso estamos mirando los puntos sobre la mediana.

6. Encuentre el rango intercuartílico. Ahora que hemos determinado Q1 y Q3 necesitamos calcular la distancia entre estas dos variables. La distancia entre Q1 y Q3 se puede encontrar restando Q1 de Q3. El valor que obtiene para el rango intercuartílico es crucial para determinar los límites de los puntos no desviados en su conjunto de datos.

7. Encuentre los `límites internos` del conjunto de datos. Puede identificar valores atípicos determinando si se encuentran dentro de una serie de límites numéricos; los llamados `valores límite internos` y `valores límite externos`. Un punto que cae fuera de los límites internos del conjunto de datos se clasifica como valor atípico leve, y un punto que queda fuera de los límites exteriores se clasifica como valor atípico extremo. Para encontrar los límites internos de su conjunto de datos, primero multiplique el rango intercuartílico por 1.5. Agregue el resultado a Q3 y réstelo de Q1. Los dos resultados son los límites internos de su conjunto de datos.


8. Encuentre los `límites exteriores` del conjunto de datos. Haces esto de la misma manera que con los límites internos, con la única diferencia de que multiplicas el rango intercuartílico por 3 en lugar de por 1,5. Luego agrega el resultado a Q3 y resta de Q1 para encontrar los límites exteriores.


9. Use una evaluación cualitativa para determinar si debe "descartar" los valores atípicos. Con el método anterior, puede determinar si ciertos puntos son valores atípicos leves, valores atípicos extremos o ningún valor atípico en absoluto. Pero no se equivoque: reconocer un punto como atípico solo lo convierte en uno candidato para ser eliminado del conjunto de datos, y no inmediatamente eliminado un punto deber convertirse en. El montó por qué un valor atípico es diferente del resto de los puntos del conjunto es crucial para determinar si se debe eliminar el valor atípico. En general, los valores atípicos causados por algún error, por ejemplo, un error en las mediciones, en los registros o en el diseño experimental, se eliminan. Por el contrario, los valores atípicos que no son causados por errores y que revelan información o tendencias nuevas e imprevistas suelen ser no eliminado.

10. Comprender la importancia de (a veces) retener los valores atípicos. Si bien algunos valores atípicos deben eliminarse de un conjunto de datos porque son el resultado de errores o porque distorsionan los resultados de manera engañosa, otros valores atípicos deben conservarse. Por ejemplo, si un valor atípico se ha obtenido correctamente (es decir, no es el resultado de un error) y/o si el valor atípico proporciona una nueva perspectiva del fenómeno que se va a medir, no debe eliminarse de inmediato. Los experimentos científicos son situaciones particularmente delicadas cuando se trata de tratar con valores atípicos: eliminar erróneamente un valor atípico puede significar descartar información importante sobre una nueva tendencia o descubrimiento.
Consejos
- Si encuentra valores atípicos, intente explicarlos antes de eliminarlos del conjunto de datos; pueden indicar errores de medición o desviaciones en la distribución.
Artículos de primera necesidad
- Calculadora
Artículos sobre el tema. "Calcular valores atípicos"
Оцените, пожалуйста статью
Popular