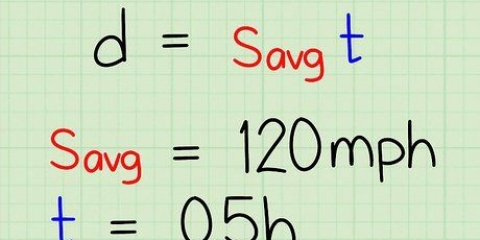Además, no olvide conectar el punto inicial con el punto final, usando una línea recta.Este es el desplazamiento que vamos a calcular. Por ejemplo, si un objeto viaja primero 300 metros en dirección este y luego 400 metros en dirección norte, se forma un triángulo rectángulo. AB es el primer lado y BC es el segundo lado del triángulo.AC es la hipotenusa del triángulo y su valor es el desplazamiento del objeto. En este ejemplo, las dos direcciones son "este" y "norte." 
Por ejemplo, x = 300 y y = 400.Tu ecuación ahora se ve así: s = √300² + 400². 
Por ejemplo: s = √90000 + 160000.s = √250000.s = 500.Ahora sabes que el desplazamiento es igual a 500 metros. 

La ecuación se verá así: s = 1/2(20 + 23)45. 
Para esta ecuación, no importa mucho si accidentalmente intercambias las velocidades inicial y final. Porque sumas estos valores primero, no importa. Pero en otras ecuaciones, intercambiar las velocidades inicial y final puede afectar la respuesta final o el valor del desplazamiento. Tu ecuación ahora se ve así: s = 1/2(43)45.Primero divide 43 por 2, lo que da como resultado 21.5. Multiplique 21,5 por 45, lo que da como resultado 967,5 metros.967,5 es el desplazamiento del coche, visto desde el punto de partida. 

Según el ejemplo anterior, su ecuación ahora debería verse así: s = 25(4) + 1/2(3)4².Sin duda, puede ayudar si pone paréntesis alrededor de los valores de aceleración y tiempo para mantener los números separados entre sí. 
Echemos un vistazo más de cerca a la ecuación: s = 25(4) + 1/2(3)4². El orden es: 4² = 16; luego 16 x 3 = 48; entonces 25 x 4 = 100; y si dura 48/2 = 24. La ecuación ahora se ve así: s = 100 + 24.Después de la suma, esto da s = 124, por lo que el desplazamiento es de 124 metros. 

Un ejemplo de una tarea: Una niña está sentada en un tiovivo. Su asiento está a una distancia de 1 metro del centro del círculo (el radio). Si la niña se mueve a lo largo de un arco circular de 1,5 metros (desplazamiento lineal), ¿cuál es su desplazamiento angular?? La ecuación se ve así: θ = 1.5/1. 
Después de la división 1.5/1 te queda 1.5.El desplazamiento angular de la niña es 1.5 radianes. Dado que el desplazamiento angular indica cuánto se ha girado un objeto desde su posición inicial, es necesario representarlo en radianes, no como una distancia. Los radianes son unidades que se utilizan para medir ángulos. 

El desplazamiento también se llama "cantidad vectorial" se refiere al cambio en la posición de un objeto en comparación con la dirección en la que se mueve el objeto. Suponga que camina 5 metros hacia el este. Si vuelves a caminar 5 metros hacia el oeste, te moverás en la dirección opuesta, de vuelta a tu punto de partida. Aunque hayas caminado un total de 10 metros, tu posición no ha cambiado y tu desplazamiento es por lo tanto de 0 metros. 
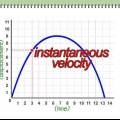
Imagínese a un entrenador de fútbol saltando de un lado a otro a lo largo de la línea de banda.Mientras da instrucciones a los jugadores, ha caminado por la línea varias veces, de ida y vuelta. Si vigilaras constantemente al entrenador, verías la distancia que recorre. Pero supongamos que el entrenador se detiene para decirle algo a un defensor? Si está en un lugar diferente de su punto de partida, entonces observa el movimiento del entrenador (en un momento determinado). 
Un camino curvo eventualmente lo llevará desde el punto de inicio hasta el punto final, pero este no es el camino más corto. Para ayudarlo a visualizar esto, imagine caminar en línea recta y ser detenido por un pilar u otro obstáculo. No puedes atravesar el pilar, así que lo rodeas. A pesar de que terminas en el mismo lugar que si hubieras atravesado el pilar, todavía tenías que recorrer un camino más largo para llegar allí. Aunque el desplazamiento es preferentemente en línea recta, es posible medir el desplazamiento de un objeto que "bien" se mueve a lo largo de un camino torcido. Esto se llama el "desplazamiento angular" y se puede calcular encontrando la distancia más corta que existe entre el punto de inicio y el punto final. 
Por ejemplo, suponga que camina 5 metros hacia el este y luego 3 metros hacia el oeste. Aunque técnicamente estás a 2 metros de tu punto de partida, el desplazamiento es -2 porque te estás moviendo en la dirección opuesta en ese punto.La distancia siempre será positiva, porque no sabes la distancia que has recorrido "deshecho" poder hacer. El desplazamiento negativo no significa que el desplazamiento disminuya. Es simplemente una forma de indicar que el movimiento es en sentido contrario. 
Entonces, esto solo es posible si te mueves en línea recta desde el punto de partida y sin cambiar de dirección después.Por ejemplo, suponga que vive en San Francisco, California y consigue un trabajo en Las Vegas, Nevada. Luego tendrá que mudarse a Las Vegas para vivir más cerca de su trabajo. Si coges el avión, un vuelo directo de San Francisco a Las Vegas, has recorrido 670 km y por tanto tu desplazamiento es de 670 km. Sin embargo, si viaja en automóvil de San Francisco a Las Vegas, su distancia puede ser de 670 km, pero ha viajado 906 km mientras tanto.Dado que conducir suele implicar un cambio de dirección (desviarse, tomar una ruta diferente), ha recorrido una distancia mucho mayor que la distancia más corta entre las dos ciudades.
Calcular desplazamiento
Contenido
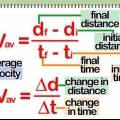
El término desplazamiento en física se refiere al cambio en lugar de un objeto. Al calcular el desplazamiento, mide cuánto se ha movido un objeto, en función de los datos de la posición inicial y la posición final. La fórmula que usa para determinar el desplazamiento depende de las variables que se dan para un problema. Siga los siguientes pasos para aprender a calcular el desplazamiento de un objeto.
Pasos
Parte 1 de 5: Cálculo del desplazamiento resultante

1. Use la fórmula para el desplazamiento resultante usando la unidad de longitud utilizada para especificar la posición inicial y final. Si bien la distancia es diferente del desplazamiento, un enunciado sobre el desplazamiento resultante indicará cuánto "metro" ha descartado un objeto. Use estas unidades de medida para calcular el desplazamiento, qué tan lejos está un objeto de su ubicación original.
- La ecuación para el desplazamiento resultante es: s = √x²+y²."s" significa desplazamiento.X es la primera dirección en la que se mueve el objeto e y es la segunda dirección en la que se mueve el objeto. Si tu objeto solo se mueve en 1 dirección, entonces y = 0.
- Un objeto solo puede moverse en un máximo de 2 direcciones, porque moverse a lo largo de la línea norte-sur o la línea este-oeste se considera neutral.

2. Conecte los puntos de acuerdo con el orden de movimiento y rotule estos puntos de la A a la Z.Usa una regla para dibujar líneas rectas de un punto a otro.

3. Ingrese los valores para x² e y².Ahora que conoce la dirección en la que se mueve su objeto, puede comenzar a completar los valores de las variables relevantes.

4. Calcula la ecuación. Calcula primero 300² y luego 400², súmalos y resta la raíz cuadrada de la suma.
Parte 2 de 5: conocer el vector de velocidad y la duración del tiempo

1. Use esta fórmula si el problema da el vector de velocidad y la duración del tiempo. Puede suceder que un problema de física no diga una palabra sobre la distancia recorrida, pero sí cuánto tiempo ha estado viajando un objeto y a qué velocidad. A continuación, puede calcular el desplazamiento utilizando la duración del tiempo y la velocidad.
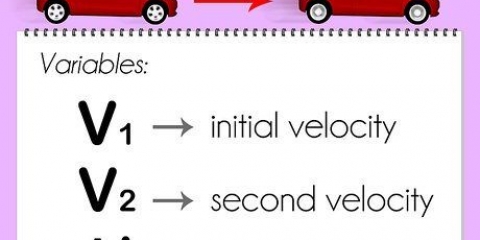
- En este caso, la ecuación se verá así: s = 1/2(u + v)t.u = la velocidad inicial del objeto, la velocidad a la que el objeto comenzó a moverse en una dirección particular.v = la velocidad final del objeto, o qué tan rápido fue al final. t = la cantidad de tiempo que tardó el objeto en llegar a su destino.
- Por ejemplo: Un coche conduce durante 45 segundos.El auto giró hacia el oeste con una velocidad de 20 m/s (velocidad inicial) y al final de la calle la velocidad es de 23 m/s (velocidad final). Calculó el desplazamiento en base a estos datos.

2. Introduzca los valores para la velocidad y el tiempo. Ahora que sabe cuánto tiempo ha estado conduciendo el automóvil y cuál fue la velocidad inicial y final, puede encontrar la distancia desde el punto inicial hasta el punto final.

3. Calcula la ecuación una vez que hayas ingresado los valores. Recuerda calcular los términos en el orden correcto o de lo contrario el desplazamiento saldrá mal.
Parte 3 de 5: Cuando se dan la velocidad, la aceleración y el tiempo

1. Se necesita otra ecuación si se da la aceleración para un problema, junto con la velocidad y el tiempo. Con una tarea de este tipo, sabes cuál ha sido la velocidad inicial del objeto, cuál es la aceleración y cuánto tiempo ha estado el objeto en la carretera. Necesitas la siguiente ecuacion.
- La ecuación para este tipo de problema se ve así: s = ut + 1/2at².El "Uds" todavía representa la velocidad inicial; El "a" es la aceleración del objeto, o también qué tan rápido cambia la velocidad del objeto. La variable"t" puede significar el tiempo total o puede indicar un período específico en el que el objeto ha acelerado. De todos modos, esto se indica en unidades de tiempo como segundos, horas, etc.
- Suponga que un automóvil con una velocidad inicial de 25 m/s gana una aceleración de 3 m/s2 durante un período de 4 segundos.¿Cuál es el desplazamiento del automóvil después de 4 segundos??

2. Complete los valores en el lugar correcto en la ecuación. A diferencia de la ecuación anterior, aquí solo se muestra la velocidad inicial, así que asegúrese de ingresar los valores correctos.

3. Calcular el desplazamiento resolviendo la ecuación. Una forma rápida de ayudarte a recordar el orden de las operaciones en una ecuación es la mnemotécnica "Sr. Dale esperando respuesta".Indica todas las operaciones aritméticas en el orden correcto (Exageración, Multiplicación, División, Elevación al cuadrado, Suma y Resta).
Parte 4 de 5: calcular el desplazamiento angular

1. Determinación del desplazamiento angular cuando un objeto se mueve a lo largo de una curva. Si bien esto aún implica calcular el desplazamiento usando una línea recta, necesita la diferencia entre la posición inicial y final a lo largo de una ruta curva.
- Tomemos como ejemplo a una niña que está en un tiovivo. Mientras gira alrededor de la parte exterior de la rueda, se mueve en un círculo. El desplazamiento angular trata de encontrar la distancia más corta entre la posición inicial y final si un objeto no se mueve en línea recta.
- La fórmula para el desplazamiento angular es: θ = S/r, por lo cual "s" representa el desplazamiento lineal, "r" para el radio y "θ" el desplazamiento angular es.El desplazamiento lineal es la distancia que recorre un objeto a lo largo de un círculo.El radio es la distancia de un objeto desde el centro del círculo.El desplazamiento angular es el valor que queremos saber.

2. Reemplaza los valores del desplazamiento lineal y el radio en la ecuación. Recuerda que el radio es la distancia desde el centro de un círculo hasta el borde; puede ser que el diametro este dado para un problema, en cuyo caso tendras que dividirlo por 2 para encontrar el radio (radius) del circulo.

3. Divide el desplazamiento lineal por el radio.Esto le dará el desplazamiento angular del objeto.
Parte 5 de 5: comprender el desplazamiento

1. Es importante entender que "distancia" a veces significa algo más que "desplazamiento."La distancia dice algo sobre qué tan lejos se ha movido un objeto en total.
- La distancia es algo que también llamamos "escalar" mencionar. Es una forma de indicar cuánta distancia has recorrido, pero no dice nada sobre la dirección en la que te has movido.
- Por ejemplo, si camina 2 metros hacia el este, 2 metros hacia el sur, 2 metros hacia el oeste y nuevamente 2 metros hacia el norte, está de vuelta en su punto de partida. Aunque has recorrido una distancia total de 10 metros, tu desplazamiento es igual a 0 metros, porque tu punto final es igual a tu punto inicial.

2. El desplazamiento es la diferencia entre dos puntos. El desplazamiento no es una suma de movimientos como ocurre con la distancia; se trata solo de la parte entre su punto de inicio y su punto final.

3. Recuerda bien las palabras "de ida y vuelta" cuando tratas de imaginar un desplazamiento. La dirección contraria deshace el movimiento en la dirección original.

4. El desplazamiento se mide a lo largo de una línea recta, no a lo largo de una trayectoria circular. Para saber el movimiento, buscas el camino más corto entre dos puntos diferentes.

5. Por favor, comprenda que el desplazamiento también puede tener un valor negativo, a diferencia de la distancia. Si se llega al punto final moviéndose en una dirección opuesta a la dirección en la que comenzó (en relación con el punto inicial), entonces su desplazamiento es negativo.

6. Darse cuenta de que los valores de distancia y desplazamiento a veces pueden ser los mismos. Si caminas en línea recta durante 25 metros y luego te detienes, la distancia que has recorrido es igual al desplazamiento, simplemente porque no has cambiado de dirección.
Consejos
- Trabajar con precisión
- No memorices las fórmulas, pero trata de entender cómo funcionan
Artículos de primera necesidad
- Calculadora
- Medidor de distancia
Artículos sobre el tema. "Calcular desplazamiento"
Оцените, пожалуйста статью
Popular