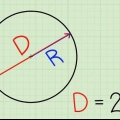
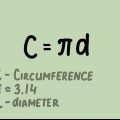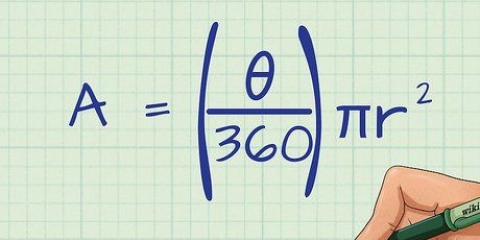El radio (r) de un círculo es la distancia desde un punto del círculo hasta el centro del círculo. El diámetro (D) de un círculo es la distancia de un punto del círculo a otro punto directamente opuesto al círculo, pasando por el centro del círculo. La letra griega pi (π) representa la relación de la circunferencia dividida por el diámetro y se representa con el número 3.14159265..., un número irracional que no tiene un dígito final ni un patrón reconocible de dígitos repetidos. Este número a menudo se redondea a 3,14 para cálculos estándar. 
En la mayoría de los problemas de matemáticas, el radio o diámetro se da. 
Por ejemplo: ¿Cuál es la circunferencia de un círculo con un radio de 3 cm? Escribe la fórmula: C = 2πr Completa las variables: C = 2π3 Multiplica: C = (2*3*π) = 6π = 18,84 cm Por ejemplo: ¿Cuál es la circunferencia de un círculo con un diámetro de 9 m? Escribe la fórmula: C = πd Completa las variables: C = 9π Multiplica: C = (9*π) = 28,26 m 
Determine la circunferencia de un círculo con un diámetro de 5 m. C = πd = 5π = 15,7 m Determine la circunferencia de un círculo con un radio de 10 m. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

El radio (r) de un círculo es la distancia desde un punto del círculo hasta el centro del círculo. El diámetro (D) de un círculo es la distancia de un punto del círculo a otro punto directamente opuesto al círculo, pasando por el centro del círculo. La letra griega pi (π) representa la relación de la circunferencia dividida por el diámetro y se representa con el número 3.14159265..., un número irracional que no tiene un dígito final ni un patrón reconocible de dígitos repetidos. Este número generalmente se redondea a 3.14 para cálculos básicos. 
En la mayoría de los problemas de matemáticas, el radio o diámetro se da. 
Por ejemplo: ¿cuál es el área de un círculo con un radio de 3 m? Escribe la fórmula: A = r. Completa las variables: A = π3. Cuadrar el radio: r = 3 = 9 Multiplicar por pi: a = 9π = 28,26 metros Por ejemplo: cual es el area de un circulo de 4 m de diametro? Escribe la fórmula: A = π(d/2). Completa las variables: A = π(4/2). Divide el diámetro por 2: d/2 = 4/2 = 2 Elevar al cuadrado el resultado: 2 = 4 Multiplicar por pi: a = 4π = 12,56 metros 
Encuentra el área de un círculo con un diámetro de 7 m. A = π(d/2) = π(7/2) = π(3,5) = 12,25 * π= 38,47 m. Hallar el area de un circulo de 3 m de radio. A = πr = π * 3 = 9 * π = 28,26 m 

Por ejemplo: calcular la circunferencia de un círculo con un radio de (x + 1). Escribe la fórmula: C = 2πr Completa la información dada: C = 2π(x+1) 
Por ejemplo: calcular la circunferencia de un círculo con un radio de (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28 Si el valor de `x` se da más adelante en el problema, puede sustituirlo y obtener un número entero. 
Encuentra el área de un círculo con un radio de 2x. A = πr = π(2x) = π4x = 12,56x Encuentra el área de un círculo con un diámetro de (x + 2). A = π(d/2) = π((x +2)/2) = ((x +2)/4)π
Cálculo de la circunferencia y el área de un círculo
Contenido
La circunferencia (C) de un círculo es su circunferencia, o la distancia alrededor de ella. El área (A) de un círculo es cuánto espacio ocupa el círculo o el área encerrada por el círculo. Tanto el área como la circunferencia se pueden calcular con fórmulas simples a partir del radio o diámetro del círculo y el valor de pi.
Pasos
Parte 1 de 3: calcular la circunferencia

1. Aprende la fórmula de la circunferencia de un círculo. Hay dos fórmulas que se pueden utilizar para calcular la circunferencia de un círculo: C = 2πr o do = re, donde π es la constante matemática y aproximadamente igual a 3.14,r es igual al radio y D igual al diámetro.
- Dado que el radio de un círculo es igual al doble de su diámetro, estas ecuaciones son esencialmente las mismas.
- Las unidades para la circunferencia pueden ser cualquier unidad para la medida de longitud: kilómetros, metros, centímetros, etc.

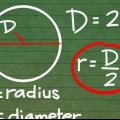
2. Comprender las diferentes partes de la fórmula. Hay tres componentes para encontrar la circunferencia de un círculo: radio, diámetro y π. El radio y el diámetro están relacionados: el radio es igual a la mitad del diámetro, mientras que el diámetro es igual al doble del radio.

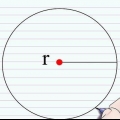
3. Medir el radio o diámetro del círculo. Coloque una regla en un borde del círculo, a través del centro y hacia el otro lado del círculo. La distancia desde el centro del círculo es el radio, mientras que la distancia desde el otro extremo del círculo es el diámetro.

4. Procesa y resuelve las variables. Una vez que haya determinado el radio y/o el diámetro del círculo, puede poner estas variables en la ecuación apropiada. Si tienes el haz, usa C = 2πr, pero si conoces el diámetro entonces usa do = re.

5. Practica con algunos ejemplos. Ahora que has aprendido la fórmula, es hora de practicar con algunos ejemplos. Cuantos más problemas resuelvas, más fácil será resolverlos en el futuro.
Parte 2 de 3: Cálculo del área

1. Aprende la formula del area de un circulo. El área de un círculo se puede calcular usando su diámetro o su radio, con dos fórmulas diferentes: A = r o A = π(d/2), donde π es la constante matemática aproximadamente igual a 3.14,r el radio y D el diámetro.
- Dado que el radio de un círculo es igual a la mitad de su diámetro, estas ecuaciones son esencialmente las mismas.
- Las unidades de área pueden ser cualquier unidad de longitud al cuadrado: km al cuadrado (km), metros al cuadrado (m), centímetros al cuadrado (cm), etc.

2. Comprender las diferentes partes de la fórmula. Hay tres componentes para encontrar la circunferencia de un círculo: radio, diámetro y π. El radio y el diámetro están relacionados entre sí: el radio es igual a la mitad del diámetro, mientras que el diámetro es igual al doble del radio.

3. Medir el radio o diámetro del círculo. Coloque un extremo de una regla en un punto del círculo, a través del centro y hacia el otro lado del círculo. La distancia desde el centro del círculo es el radio, mientras que la distancia desde el otro punto del círculo es el diámetro.

4. Completa las variables y resuélvelas. Una vez que haya determinado el radio y/o el diámetro del círculo, puede conectar estas variables en la ecuación apropiada. Si conoce el radio, utilice A = r, pero si conoces el diámetro entonces usa A = π(d/2).

5. Practica con algunos ejemplos. Ahora que has aprendido la fórmula, es hora de practicar con algunos ejemplos. Cuantos más problemas resuelvas, más fácil será resolver otros problemas.
Parte 3 de 3: calcular el área y el perímetro con variables

1. Determinar el radio o diámetro del círculo. Algunos problemas dan un radio o diámetro con una variable, como r = (x + 7) o d = (x + 3). En este caso, aún puede determinar el área o el perímetro, pero su respuesta final también contendrá esa variable. Anote el radio o diámetro como se indica en la declaración.
- Por ejemplo: calcular la circunferencia de un círculo con un radio de (x = 1).

2. Escribe la fórmula con la información dada. Ya sea que desee calcular el área o el perímetro, aún debe seguir los pasos básicos para completar lo que sabe. Escriba la fórmula para el área o el perímetro y luego complete las variables dadas.

3. Resolver el problema como si la variable fuera un número. En este punto, puede resolver el problema como lo haría normalmente, tratando la variable como si fuera un número más. Es posible que necesite el usando la propiedad distributiva para simplificar la respuesta final.

4. Practica con algunos ejemplos. Ahora que has aprendido la fórmula, es hora de practicar con algunos ejemplos. Cuantos más problemas resuelva, más fácil será resolver otros nuevos.
Artículos sobre el tema. "Cálculo de la circunferencia y el área de un círculo"
Оцените, пожалуйста статью
Popular