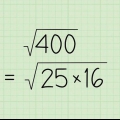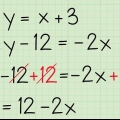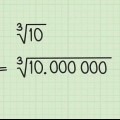es `el valor absoluto de 2.`
es `el valor absoluto de 2.`



Asignación:
Simplificar entre paréntesis:
Suma y resta:
Haz que todo lo que esté dentro del valor absoluto sea positivo:
Respuesta final: 19 
Asignación:
Haz el orden de las operaciones dentro y fuera del valor absoluto:
Determinar los valores absolutos:
Orden de operaciones:
Simplifica la respuesta final: 

 =
= 
 =
= 
 =
= 


 = (1, 6)
= (1, 6) = (2, -1)
= (2, -1) = (-8, 6)
= (-8, 6)

Coeficientes: (3, -4) Fórmula de distancia:
Elevar al cuadrado los coeficientes: ` 
Prestar atención: Practica de nuevo la fórmula de la distancia si no la entiendes. Tenga en cuenta que elevar al cuadrado ambos números los hace positivos, esencialmente brindándole el valor absoluto. 
Coeficientes: (3, -4) Fórmula de distancia:
Elevar al cuadrado los coeficientes:
Suma el producto de los coeficientes:

Coeficientes: (3, -4) Fórmula de distancia:
Elevar al cuadrado los coeficientes:
Suma el producto de los coeficientes:
Resta la raíz cuadrada para la respuesta final: 5 

 = √37
= √37 = √5
= √5 = 10
= 10
Calcular el valor absoluto de un número
Contenido
El valor absoluto de un número es fácil de encontrar y la teoría detrás de él es importante para resolver ecuaciones con un valor absoluto. Cada valor absoluto es una medida de qué tan lejos está ese número de cero. Si piensas en una recta numérica, con el cero en el medio, puedes averiguar qué tan lejos está el número en cuestión de ese cero.
Pasos
Método 1 de 2: determinar el valor absoluto

1. Recuerda que el valor absoluto es la distancia de un número al cero. Un valor absoluto es la distancia del número al cero a lo largo de una recta numérica. cualquiera, así que simplemente indica qué tan lejos está -4 de cero. Dado que la distancia siempre es un número de posición (no puede moverse en pasos `negativos`, solo en una dirección diferente), el resultado del valor absoluto siempre es positivo.
así que simplemente indica qué tan lejos está -4 de cero. Dado que la distancia siempre es un número de posición (no puede moverse en pasos `negativos`, solo en una dirección diferente), el resultado del valor absoluto siempre es positivo.
 así que simplemente indica qué tan lejos está -4 de cero. Dado que la distancia siempre es un número de posición (no puede moverse en pasos `negativos`, solo en una dirección diferente), el resultado del valor absoluto siempre es positivo.
así que simplemente indica qué tan lejos está -4 de cero. Dado que la distancia siempre es un número de posición (no puede moverse en pasos `negativos`, solo en una dirección diferente), el resultado del valor absoluto siempre es positivo.
2. Hacer que el número dentro de las barras de valor absoluto sea positivo. En pocas palabras, el valor absoluto hace que cualquier número sea positivo. Es útil para medir distancias, o determinar valores en materia financiera, trabajando con números negativos como deuda o préstamos.

3. Use barras verticales simples para indicar un valor absoluto. El formato para un valor absoluto es fácil. Líneas simples (que se encuentran cerca de la tecla Intro en un teclado) alrededor de un número o expresión, como  , indica un valor absoluto.
, indica un valor absoluto.
 , indica un valor absoluto.
, indica un valor absoluto. es `el valor absoluto de 2.`
es `el valor absoluto de 2.`
4. Omita los signos menos para el número dentro de las marcas de valor absoluto. Por ejemplo: |-5| luego se convierte en |5|.

5. Omitir las marcas de valor absoluto. El número que queda es la respuesta, entonces |-5| se convierte en |5| y luego 5. Lo siguiente es todo lo que necesita hacer:


6. Simplifica la expresión dentro del valor absoluto. ¿Es una expresión simple, como  , entonces puedes hacerlo positivo. Pero una expresión como
, entonces puedes hacerlo positivo. Pero una expresión como  debe simplificarse antes de poder encontrar su valor absoluto. El orden fijo de las operaciones todavía se aplica:
debe simplificarse antes de poder encontrar su valor absoluto. El orden fijo de las operaciones todavía se aplica:
 , entonces puedes hacerlo positivo. Pero una expresión como
, entonces puedes hacerlo positivo. Pero una expresión como  debe simplificarse antes de poder encontrar su valor absoluto. El orden fijo de las operaciones todavía se aplica:
debe simplificarse antes de poder encontrar su valor absoluto. El orden fijo de las operaciones todavía se aplica:




7. Utilice siempre este orden de operaciones antes de calcular el valor absoluto. Cuando resuelves ecuaciones más largas, haces todo el trabajo requerido antes de determinar el valor absoluto. No intentes simplificar valores absolutos hasta que todo esté sumado, restado y dividido correctamente. Por ejemplo:






8. Sigue trabajando en algunos ejercicios de muestra para dominarlo. Calcular el valor absoluto de un número es muy fácil, pero eso no significa que hacer problemas de práctica no sea útil para refrescar tus conocimientos:
 =
= 
 =
= 
 =
= 
Método 2 de 2: Resolver ecuaciones complejas con valores absolutos (ecuaciones con `i`)

1. Tenga cuidado cuando trate con ecuaciones complejas que involucran números imaginarios, como `i` o - 1  , y resolverlos por separado. No puedes encontrar el valor absoluto de números imaginarios de la misma manera que puedes encontrar números racionales. Puedes encontrar el valor absoluto de una ecuación compleja resolviéndola en la fórmula de la distancia. Toma la expresión
, y resolverlos por separado. No puedes encontrar el valor absoluto de números imaginarios de la misma manera que puedes encontrar números racionales. Puedes encontrar el valor absoluto de una ecuación compleja resolviéndola en la fórmula de la distancia. Toma la expresión  como ejemplo.
como ejemplo.
 , y resolverlos por separado. No puedes encontrar el valor absoluto de números imaginarios de la misma manera que puedes encontrar números racionales. Puedes encontrar el valor absoluto de una ecuación compleja resolviéndola en la fórmula de la distancia. Toma la expresión
, y resolverlos por separado. No puedes encontrar el valor absoluto de números imaginarios de la misma manera que puedes encontrar números racionales. Puedes encontrar el valor absoluto de una ecuación compleja resolviéndola en la fórmula de la distancia. Toma la expresión  como ejemplo.
como ejemplo. - Asignación:
- Prestar atención: Si usas una expresión como
puedes reemplazarlo con `i.` La raíz cuadrada de -1 es un número imaginario, yo.

2. Encuentra los coeficientes de la ecuación compleja. Toma 3-4i como la ecuación de una recta. El valor absoluto es la distancia a cero, por lo que determina la distancia a cero para el punto (3, -4) en esta línea.Los coeficientes son simplemente los dos números que no son `i`. Aunque el número al lado de la i suele ser el segundo número, no importa al resolver. Practica esto con los siguientes coeficientes:
 = (1, 6)
= (1, 6) = (2, -1)
= (2, -1) = (-8, 6)
= (-8, 6)
3. Eliminar los símbolos de valor absoluto de la ecuación. Ahora solo necesitas los coeficientes. Recuerda que tú determinas la distancia de la ecuación desde cero. Dado que utilizará la fórmula de distancia en el próximo paso, esto es lo mismo que determinar el valor absoluto.

4. Cuadrar ambos coeficientes. Para determinar la distancia, usas la fórmula de la distancia, también conocida como  . Entonces, como primer paso, debe elevar al cuadrado ambos coeficientes de la ecuación compleja. Seguimos con el ejemplo:
. Entonces, como primer paso, debe elevar al cuadrado ambos coeficientes de la ecuación compleja. Seguimos con el ejemplo:  :
:
 . Entonces, como primer paso, debe elevar al cuadrado ambos coeficientes de la ecuación compleja. Seguimos con el ejemplo:
. Entonces, como primer paso, debe elevar al cuadrado ambos coeficientes de la ecuación compleja. Seguimos con el ejemplo:  :
:


5. Coloca el producto de los números debajo del radical. El signo radical indica que estás restando la raíz cuadrada del número que está debajo. Ahora sume los números primero, sin hacer nada con el signo radical.




6. Saque la raíz cuadrada para su respuesta final. Solo necesitas simplificar la ecuación para la respuesta final. Esta es la distancia desde su `punto` en una recta numérica imaginaria hasta el punto cero. Si no hay raíz cuadrada, simplemente deje la respuesta del último paso debajo del signo radical: esta es una respuesta correcta.





7. Pruebe algunos ejercicios de práctica. Haga clic con el mouse directamente detrás de las preguntas para ver las respuestas, en blanco.
 = √37
= √37 = √5
= √5 = 10
= 10Consejos
- Si tiene una variable dentro de un valor absoluto, no puede eliminar los signos de valor absoluto con este método, porque si el valor de la variable es negativo, entonces el valor absoluto lo haría positivo.
- Si tiene una expresión dentro de un valor absoluto, simplifique la expresión antes de determinar su valor absoluto.
- Cuando un número positivo está dentro de los marcadores de valor absoluto, la respuesta siempre es ese número.
- Necesita un método diferente para resolver ecuaciones de valor absoluto con una x y una y, aunque la teoría detrás del valor absoluto se usa como base.
- Un valor absoluto nunca puede ser un número negativo, por lo que si ve algo como | 2 - 4x| = -7, entonces sabes que esta ecuación es falsa sin tener que resolverla.
Artículos sobre el tema. "Calcular el valor absoluto de un número"
Оцените, пожалуйста статью
Popular