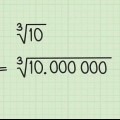Otros juegos pueden requerir que elijas entre cinco o seis números, o más, de un grupo de números más grande o más pequeño. 


Entonces, su probabilidad de elegir correctamente los primeros cinco números y el Powerball es 1 en 292.201.338. 

Por ejemplo, su probabilidad de ganar tres de cinco números de un grupo de 69 se describe mediante la ecuación  .
. 
En el ejemplo, esto se convierte en 579,76. Por lo tanto, su probabilidad de elegir correctamente tres de cinco es de 1 en 579,76. 


Sin embargo, algunas loterías pagan más que otras. Por ejemplo, en un momento, el boleto de lotería de $1 de la lotería Take Five de Nueva York tenía un valor esperado igual a su costo. Esto significaba que al jugar esta lotería, los jugadores podían esperar no perder. 

En otras palabras: si compra diez boletos de lotería al día, tiene un 50 por ciento de posibilidades de ganar si compra este 49.300 años sigue haciendo. Sin embargo, esto no significa que comprar dos boletos ese día garantizaría una victoria. Su probabilidad total de ganar sigue siendo de alrededor del 50 por ciento.
Calcular probabilidades de lotería
Contenido
Todo el mundo ha oído comparaciones sobre las probabilidades de ganar la lotería frente a las probabilidades de otros eventos poco probables, como que te caiga un rayo. Es cierto, las probabilidades de ganar el premio mayor en un juego como Powerball o cualquier otra lotería pick-6 son increíblemente bajas. pero que bajo? ¿Y con qué frecuencia tienes que jugar para aumentar tus posibilidades?? Estas respuestas se pueden encontrar exactamente con algunos cálculos simples.
Pasos
Método 1 de 3: Cálculo de las probabilidades del premio mayor

1. Comprender los cálculos utilizados. Las probabilidades de ganar una lotería donde los números se eligen de una secuencia, independientemente del orden, están definidas por la fórmula  . En esta fórmula, n representa el número total de números posibles y r representa el número de números que se elegirán. el `!` significa factorial, donde para cada entero n es n*(n-1)*(n-2)... etc., hasta llegar a 0. Por ejemplo: 3! entonces significa
. En esta fórmula, n representa el número total de números posibles y r representa el número de números que se elegirán. el `!` significa factorial, donde para cada entero n es n*(n-1)*(n-2)... etc., hasta llegar a 0. Por ejemplo: 3! entonces significa  .
.
 . En esta fórmula, n representa el número total de números posibles y r representa el número de números que se elegirán. el `!` significa factorial, donde para cada entero n es n*(n-1)*(n-2)... etc., hasta llegar a 0. Por ejemplo: 3! entonces significa
. En esta fórmula, n representa el número total de números posibles y r representa el número de números que se elegirán. el `!` significa factorial, donde para cada entero n es n*(n-1)*(n-2)... etc., hasta llegar a 0. Por ejemplo: 3! entonces significa  .
. - Un ejemplo sencillo: imagina que tienes que elegir entre dos números y los números del 1 al 5. Su probabilidad de elegir los dos números `correctos` (los números ganadores) se definiría entonces como
.
- Esto entonces se resuelve como
, cualquiera
, y son 10.
- Así que tu probabilidad de ganar este juego es de 1 en 10.
- Calcular el factorial puede volverse confuso, especialmente cuando se trata de números más grandes. La mayoría de las calculadoras tienen una función factorial para facilitar un poco estos cálculos. Alternativamente, también puede ingresar la facultad en los motores de búsqueda de Duck Duck Go (como, por ejemplo,. `55!`) o Google, para obtener la respuesta.

2. Determinar las reglas de la lotería. La mayoría de los millones de dinero, Powerball y otras loterías importantes, usan aproximadamente las mismas reglas. Se eligen cinco o seis números de una gran cantidad de números, en orden aleatorio. Los números no se pueden repetir. En algunos juegos, se agrega un número fijo al final (el Powerball en los juegos de Powerball es un ejemplo). Las reglas estándar de Powerball muestran que se eligen cinco números (sin incluir el Powerball) de 69 números posibles.

3. Aplicar los números a la ecuación para la probabilidad. La primera parte de la probabilidad de Powerball se calcula como la probabilidad de elegir correctamente los primeros cinco números. Esto se calcula convenientemente con la fórmula de probabilidad introducida anteriormente. Entonces la ecuación para estas líneas en particular se convierte en:  , para simplificar a
, para simplificar a  .
.
 , para simplificar a
, para simplificar a  .
.
4. Calcula tu probabilidad de elegir el número correcto. Es mejor resolver la ecuación con un motor de búsqueda o una calculadora, ya que los números utilizados son difíciles de escribir entre los pasos. Una vez resuelta, la ecuación será el número 11.238.dar 513. Esto significa que tienes una probabilidad de 1 en 11.238.513 para elegir los cinco números correctamente.

5. Multiplica para obtener el número final. Para tener en cuenta la probabilidad de elegir correctamente el Powerball y ganar el premio mayor, simplemente deberá multiplicar el número del resultado anterior por el tamaño del pozo de Powerball. Para el juego estándar, hay 26 números posibles de Powerball. Así que multiplicas el resultado anterior (11.238.513 en este caso) con el número final (que es 26), para calcular tu probabilidad final (que es 292.201.338).
Método 2 de 3: determinar la probabilidad de premios más pequeños

1. Comience con la oportunidad del premio mayor. En la mayoría de los casos, hay premios más pequeños disponibles que requieren que elija algunos de los números correctamente. Escogiendo tres o cuatro de los números ganadores puedes ganar una cantidad de cientos de miles de euros. En este caso, sus probabilidades se basan en calcular la probabilidad de elegir un par de números correctos, combinados con un número opuesto de números incorrectos. Esto requiere que sepas primero el número total de combinaciones posibles. Estos se pueden describir con las probabilidades de elegir correctamente todos los números ganadores.
- Primero debe haber calculado las probabilidades del premio mayor como se describe en el método `Cálculo de las probabilidades del premio mayor`.
- Para simplificar los cálculos, usamos la probabilidad de elegir correctamente los primeros cinco números de Powerball. En el otro método calculamos que esto es 1 en 11.238.513 es.

2. escribe la ecuacion. Su oportunidad de ganar `k` de la cantidad de números `r` del grupo total de números `n` se puede definir como:  . Esta fórmula parece mucho más complicada, pero en realidad no es más que tres copias de la ecuación de probabilidad simple del otro método. Simplemente complete sus números para n, r y k.
. Esta fórmula parece mucho más complicada, pero en realidad no es más que tres copias de la ecuación de probabilidad simple del otro método. Simplemente complete sus números para n, r y k.
 . Esta fórmula parece mucho más complicada, pero en realidad no es más que tres copias de la ecuación de probabilidad simple del otro método. Simplemente complete sus números para n, r y k.
. Esta fórmula parece mucho más complicada, pero en realidad no es más que tres copias de la ecuación de probabilidad simple del otro método. Simplemente complete sus números para n, r y k. .
.
3. Determina tu oportunidad de ganar. Al igual que con la ecuación básica, esta ecuación se resuelve mejor ingresando todo en una calculadora o motor de búsqueda, ya que algunos de los números intermedios del cálculo son demasiado grandes para escribirlos. Si se resuelve correctamente, el resultado será la probabilidad de que tres de los cinco números de Powerball sean elegidos correctamente.

4. Elija el número deseado de números ganadores. Puede ajustar su cálculo cambiando el valor de k para determinar la probabilidad de ganar diferentes secuencias de los cinco números. Su probabilidad de ganar disminuirá a medida que k crezca y viceversa.
Método 3 de 3: calcular otras probabilidades de lotería

1. Determinar el valor esperado de un billete de lotería. El valor esperado de un billete de lotería representa el premio teórico de un billete. En otras palabras, es la cantidad que teóricamente podrías recuperar después de comprar un boleto de lotería. Se puede calcular multiplicando las probabilidades de un pago determinado (premio mayor, 4 números correctos, 3 números correctos, etc.) con el monto del pago, luego súmalos. Sin embargo, este número está claramente distorsionado por el enorme premio mayor.
- Por lo general, su pago será mucho menor que el valor esperado.
- En el estándar 5+1 de 69 y 26 Powerball, el valor esperado de un boleto es de aproximadamente $1.78.

2. Compare el costo con el valor esperado. Puede determinar los beneficios esperados de jugar a la lotería comparando el valor esperado de un boleto con el costo de un boleto. Por lo general, será mucho menos. Además, su beneficio real difiere mucho del valor esperado, a pesar del nombre. La mayoría de las personas obtienen solo una fracción del valor esperado ideal, si es que obtienen algo.

3. Determinar el aumento de posibilidades jugando varias veces. Jugar a la lotería varias veces puede aumentar su probabilidad promedio de ganar, sin importar cuán pequeña sea. Es más fácil imaginar este aumento como una disminución en la posibilidad de perder. Por ejemplo, si su probabilidad promedio de ganar es de 1 en 250.000.000, entonces tu probabilidad de perder un sorteo es  , y eso equivale a un número muy cercano a 1 (0.99999...). Si juegas dos veces, entonces el número se eleva al cuadrado (
, y eso equivale a un número muy cercano a 1 (0.99999...). Si juegas dos veces, entonces el número se eleva al cuadrado ( ), creando un número ligeramente inferior a 1 (y por lo tanto una mayor posibilidad de ganar).
), creando un número ligeramente inferior a 1 (y por lo tanto una mayor posibilidad de ganar).
 , y eso equivale a un número muy cercano a 1 (0.99999...). Si juegas dos veces, entonces el número se eleva al cuadrado (
, y eso equivale a un número muy cercano a 1 (0.99999...). Si juegas dos veces, entonces el número se eleva al cuadrado ( ), creando un número ligeramente inferior a 1 (y por lo tanto una mayor posibilidad de ganar).
), creando un número ligeramente inferior a 1 (y por lo tanto una mayor posibilidad de ganar).
4. Encuentra el número de veces que tienes que jugar para tener una buena oportunidad de ganar. La mayoría de los jugadores de lotería están convencidos de que si juegan con la suficiente frecuencia, pueden aumentar significativamente sus probabilidades de ganar. Es cierto que jugando más a menudo tienes más posibilidades de ganar. Sin embargo, este aumento no es significativo durante mucho tiempo. Por ejemplo, dadas las probabilidades anteriores (1 en 250 millones por juego), debe jugar aproximadamente 180 millones de veces para tener una probabilidad de 50-50 de ganar.
Consejos
- No se deje engañar por estafas de lotería en las que alguien afirma tener una forma garantizada de ganar. Si alguien tuviera una forma garantizada de ganar, realmente no se detendrían diciéndote.
- Cualquier conjunto de números tiene exactamente las mismas probabilidades que cualquier otro conjunto. Por lo tanto, 32-45-22-19-09-11 es tan probable como 1-2-3-4-5-6.
Advertencias
- Si cree que tiene un problema con el juego, probablemente lo tenga. Jugadores Anónimos es una gran fuente de información y ayuda para las personas que se enfrentan a la adicción al juego.
- No juegue más de lo que puede permitirse perder.
Artículos sobre el tema. "Calcular probabilidades de lotería"
Оцените, пожалуйста статью
Similar
Popular