Calcular la apotema de un hexágono: 15 pasos (con fotos)

Contenido

Pasos
- Método 1 de 2: Usando el teorema de Pitágoras (se da la longitud del radio)
- Método 2 de 2: usar trigonometría (y un radio dado)
Consejos

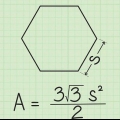
Un hexágono es un polígono con seis ángulos y lados. Cuando un hexágono es regular, tiene seis lados iguales y una apotema. Una apotema es un segmento de línea desde el centro de un polígono hasta el centro de cada lado. Normalmente se debe dar la longitud de la apotema para calcular el área de un hexágono. Siempre que sepa la longitud del lado del hexágono, puede calcular la longitud de la apotema.

Pasos

Método 1 de 2: Usando el teorema de Pitágoras (se da la longitud del radio)

Imagen titulada Calcular la apotema de un hexágono Paso 1

1. Divide el hexágono en seis triángulos equiláteros congruentes. Para ello, dibuja una línea desde cada vértice o punto, hasta el vértice opuesto.

Imagen titulada Calcular la apotema de un hexágono Paso 2

2. Elige un triángulo y escribe la longitud de la base. es igual a la longitud del lado del hexágono.

Por ejemplo, tienes un hexágono con una longitud de 8 cm para el lado. La base de cualquier triángulo equilátero es por lo tanto 8 cm.

Imagen titulada Calcular la apotema de un hexágono Paso 3

3. Haz dos triángulos rectángulos. Lo haces dibujando una línea desde el vértice superior del triángulo equilátero perpendicular a la base. Esta línea dividirá en dos la base del triángulo (por lo que es la apotema del hexágono). Rotula la longitud de la base de uno de los triángulos rectángulos.

Por ejemplo, si la base del triángulo equilátero mide 8 cm, entonces la base de cualquier triángulo rectángulo, cuando divides el triángulo en dos triángulos rectángulos, ahora es igual a 4 cm.

Imagen titulada Calcular la apotema de un hexágono Paso 4

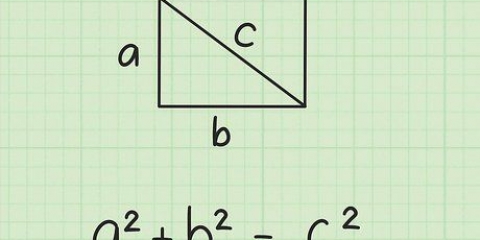
4. Usa el teorema de Pitágoras. la fórmula es

a 2 + B^{2} = C^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , por lo cual

C

$C$ es igual a la longitud de la hipotenusa (el lado opuesto al ángulo recto), y

a

$a$ y

B

$B$ ser igual a las longitudes de los otros dos lados del triángulo.

Por ejemplo, si el triángulo rectángulo tiene una hipotenusa de

2

$2$ un lado de

1

$1$ y otro lado de aproximadamente

1, 732

$1,732$ (

\sqrt{3}

${ sqrt{3}}$ ), entonces el teorema de Pitágoras establece que

12 + {\sqrt{3}}^{2} = 2^{2}

$1^{{2}}+{raíz cuadrada{3}}^{{2}}=2^{{2}}$ , lo cual es correcto cuando resuelves esto:

1 + 3 = 4

$1+3=4$ .

Imagen titulada Calcular la apotema de un hexágono Paso 5

5. Sustituye la longitud de la base del triángulo rectángulo en la fórmula. Substituto para

B

$B$ .

Por ejemplo, si la longitud de la base es 4, tu fórmula se vería así:

a 2 + 4^{2} = C^{2}

$a^{{2}}+4^{{2}}=c^{{2}}$ .

Imagen titulada Calcular la apotema de un hexágono Paso 6

6. Sustituye la longitud de la hipotenusa en la fórmula. Conoces la longitud de la hipotenusa porque conoces la longitud del hexágono. La longitud del lado de un hexágono regular es igual al radio del hexágono. El radio es una línea que une el centro de un polígono con uno de sus vértices. Verás que la hipotenusa del triángulo rectángulo es también el radio del hexágono, por lo que la longitud del lado del hexágono es igual a la longitud de la hipotenusa.

Por ejemplo, si la longitud del lado del hexágono es de 8 cm, entonces la longitud de la hipotenusa del triángulo rectángulo también es de 8 cm. Entonces su fórmula ahora se verá así:

a 2 + 4^{2} = 8^{2}

$a^{{2}}+4^{{2}}=8^{{2}}$ .

Imagen titulada Calcular la apotema de un hexágono Paso 7

7. Elevar al cuadrado los valores conocidos de la fórmula. Recuerda que elevar al cuadrado un número es lo mismo que multiplicar ese número por sí mismo.

Por ejemplo, después de elevar al cuadrado los valores conocidos, su fórmula se verá así:

a 2 + dieciséis = 64

$a^{{2}}+16=64$ .

Imagen titulada Calcular la apotema de un hexágono Paso 8

8. Aislar la variable desconocida. Lo haces restando el valor al cuadrado

B

$B$ de ambos lados de la ecuación.

Por ejemplo:

a 2 + dieciséis - dieciséis = 64 - dieciséis

$a^{{2}}+16-16=64-16$

a 2 = 48

$un^{{2}}=48$

Imagen titulada Calcular la apotema de un hexágono Paso 9

9. Resolver a{ estilo de visualización a} $a$ . Lo haces determinando la raíz cuadrada de cada lado de la ecuación. Esto te dará la longitud del lado faltante del triángulo, que es igual a la longitud de la apotema del hexágono.

Por ejemplo, usando una calculadora se calcula

\sqrt{48} = 6, 93

${sqrt{48}}=6,93$ . Entonces, la longitud faltante del triángulo rectángulo, y por lo tanto la longitud de la apotema del hexágono, es igual a 6,93 cm.

Método 2 de 2: usar trigonometría (y un radio dado)

Imagen titulada Calcular la apotema de un hexágono Paso 10

1. Escribe la fórmula para encontrar la apotema de un polígono regular. la fórmula es

apotema = s 2 broncearse (\frac{180}{norte})

${text{apotema}}={frac{s}{2tan({frac{180}{n}})}}$ , por lo cual

s

$s$ es igual a la longitud del lado del polígono y

norte

$norte$ es igual al número de lados del polígono.

Imagen titulada Calcular la apotema de un hexágono Paso 11

2. Sustituye la longitud del lado en la fórmula. No olvides sustituir la variable

s

$s$ .

Por ejemplo, para un hexágono con una longitud de lado de 8 cm, la fórmula se vería así:

8 2 broncearse (\frac{180}{norte})

${frac{8}{2tan({frac{180}{n}})}}$ .

Imagen titulada Calcular la apotema de un hexágono Paso 12

3. Ingrese el número de lados en la fórmula. Un hexágono tiene 6 lados. No olvides sustituir la variable

norte

$norte$ .

Por ejemplo:

8 2 broncearse (\frac{180}{6})

${frac{8}{2tan({frac{180}{6}})}}$ .

Imagen titulada Calcular la apotema de un hexágono Paso 13

4. Redondea el cálculo entre paréntesis. Esto le da el número de grados necesarios para calcular la tangente.

Por ejemplo,

\frac{180}{6} = 30

${frac{180}{6}}=30$ , con lo cual la fórmula ahora queda así:

8 2 broncearse (30)

${frac{8}{2tan(30)}}$ .

Imagen titulada Calcular la apotema de un hexágono Paso 14

5. Determinar la tangente. Use una calculadora o tabla trigonométrica para esto.

Por ejemplo, la tangente de 30 es aproximadamente 0,577, por lo que la fórmula se vería así:

8 2 (0, 577)

${frac{8}{2(0,577)}}$ .

Imagen titulada Calcular la apotema de un hexágono Paso 15

6. Multiplique la tangente por 2 y luego divida la longitud de un lado por este número. Con esto has calculado la longitud de la apotema de tu hexágono.

Por ejemplo:

apotema = 8 2 (0, 577)

${text{apotema}}={frac{8}{2(0,577)}}$

apotema = 8 1, 154

${text{apotema}}={frac{8}{1,154}}$

apotema = 6, 93

${text{apotema}}=6,93$
Entonces la apotema de un hexágono regular con lados de 8 cm es de aproximadamente 6,93 cm.

Consejos

El término `apotema` puede referirse al segmento de línea real o a la longitud de ese segmento de línea.
Recuerda que este método solo funciona con hexágonos regulares. Los hexágonos irregulares no tienen apotema.