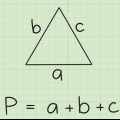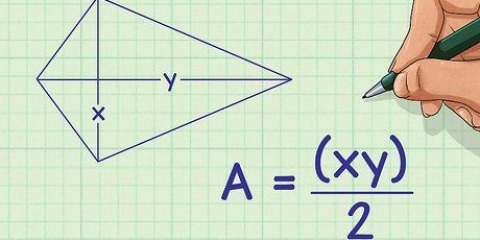Por ejemplo, si tiene un trapezoide con una parte superior de 2 cm, una parte inferior de 3 cm y dos lados de 1 cm, su fórmula se vería así:


Por ejemplo:


Por lo tanto, la circunferencia del trapezoide es de 7 cm. 

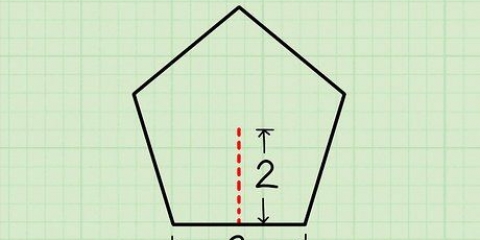
Por ejemplo, si tiene un trapezoide con una altura de 6 cm, debe dibujar una línea desde cada vértice superior hasta el inferior. Nota 6 cm por cada línea. 
Por ejemplo, si la parte superior del trapezoide mide 6 cm, entonces la parte media de la parte inferior también mide 6 cm. 

Por ejemplo, si sabes que la altura del trapezoide es de 6 cm y la longitud del lado (hipotenusa) es de 9 cm, tu ecuación se vería así:


Por ejemplo: es la ecuación  , luego elevas al cuadrado 6 y 9, y restas el cuadrado de 6 al cuadrado de 9:
, luego elevas al cuadrado 6 y 9, y restas el cuadrado de 6 al cuadrado de 9:




Por ejemplo:




Así que toma nota como base del primer triangulo.
como base del primer triangulo. 
Por ejemplo, si el segundo lado del trapezoide mide 7 cm, calcula de la siguiente manera:





Así que toma nota como la base del segundo triangulo.
como la base del segundo triangulo. 
Por ejemplo: 
Después de convertir las raíces cuadradas a decimales, tienes
Entonces, la circunferencia aproximada de tu trapezoide es 38.314 cm.. 

Por ejemplo, si tiene un trapezoide con una altura de 6 cm, dibuje una línea desde cada vértice superior hasta el inferior. Tenga en cuenta 6 cm en cada línea. 
Por ejemplo, si la parte superior del trapezoide mide 6 cm, entonces la parte media de la parte inferior también mide 6 cm. 
Con esta razón puedes encontrar la longitud de la hipotenusa del triángulo, que también es el primer lado del trapezoide. La hipotenusa es el lado opuesto al ángulo de 90 grados de un triángulo rectángulo. 
Suponga que el ángulo interior dado es de 35 grados y la altura del triángulo es de 6 cm, entonces su fórmula se verá así:


Por ejemplo, usando una calculadora encontrarás que el seno de un ángulo de 35 grados es 0.5738 (redondeado). Así que tu fórmula es ahora:


Por ejemplo:




Por lo tanto, la longitud de la hipotenusa y el primer lado faltante del trapecio es de aproximadamente 10,4566 cm. 
Por ejemplo, si el ángulo interior dado es de 45 grados, calcula:





Entonces, la longitud de la hipotenusa y el segundo lado faltante del trapezoide es de aproximadamente 8,4854 cm. 

Por ejemplo, si el primer triángulo rectángulo tiene una hipotenusa de 10,4566 y una altura de 6, tu fórmula es:


Por ejemplo:






Entonces, la base del triángulo y la primera parte que falta en la parte inferior del trapezoide mide aproximadamente 8,5639 cm. 
Por ejemplo, si el segundo triángulo rectángulo tiene una hipotenusa de 8,4854 y una altura de 6, lo calcularías de la siguiente manera:






Entonces, la base del segundo triángulo y la segunda parte que falta en la parte inferior del trapezoide es igual a 6 cm. 
Por ejemplo: 
Entonces la circunferencia aproximada del trapezoide es 45.5059 cm.
Calcular el perímetro de un trapezoide
Contenido
Un trapezoide se define como un cuadrilátero con dos lados paralelos. Al igual que con cualquier polígono, debe sumar los cuatro lados para encontrar el perímetro de un trapezoide (o trapezoide). A menudo, sin embargo, perderá las longitudes de los lados, pero tiene otros datos, como la altura del trapezoide o las medidas de los ángulos. Usando estos datos, puedes encontrar las longitudes desconocidas de los lados usando las reglas de geometría y trigonometría.
Pasos
Método 1 de 3: si conoces la longitud de ambos lados y la base

1. Establecer la fórmula para la circunferencia de un trapecio. la fórmula es  , por lo cual
, por lo cual  es igual al perímetro del trapezoide, y la variable
es igual al perímetro del trapezoide, y la variable  es igual a la longitud de la parte superior del trapezoide,
es igual a la longitud de la parte superior del trapezoide,  es igual a la longitud de la base,
es igual a la longitud de la base,  es igual a la longitud del lado izquierdo y
es igual a la longitud del lado izquierdo y  es igual a la longitud del lado derecho.
es igual a la longitud del lado derecho.
 , por lo cual
, por lo cual  es igual al perímetro del trapezoide, y la variable
es igual al perímetro del trapezoide, y la variable  es igual a la longitud de la parte superior del trapezoide,
es igual a la longitud de la parte superior del trapezoide,  es igual a la longitud de la base,
es igual a la longitud de la base,  es igual a la longitud del lado izquierdo y
es igual a la longitud del lado izquierdo y  es igual a la longitud del lado derecho.
es igual a la longitud del lado derecho.
2. Usa las longitudes de los lados en la fórmula. Si no conoce la longitud de los cuatro lados del trapezoide, no puede usar esta fórmula.


3. Suma las longitudes de los lados. Esto te dará la circunferencia de tu trapezoide.


Por lo tanto, la circunferencia del trapezoide es de 7 cm.
Método 2 de 3: si conoce la altura, las longitudes de ambos lados y la longitud superior

1. Divide el trapezoide en un rectángulo y dos triángulos rectángulos. Para hacer esto, dibuje la altura desde ambas esquinas superiores.
- Si no puedes formar los dos triángulos rectángulos porque un lado del trapezoide es perpendicular a la base, asegúrate de que este lado tenga la misma longitud que la altura y divide el trapezoide en un rectángulo y un triángulo rectángulo.

2. Dar la longitud de cada línea de contorno. Como estos son los lados opuestos de un rectángulo, tendrán la misma longitud.

3. Tenga en cuenta la longitud de la parte media de la parte inferior. (Esta es la parte inferior del rectángulo.) La longitud será igual a la longitud de la parte superior (la parte superior del rectángulo), porque los lados opuestos de un rectángulo tienen la misma longitud. Si no conoce la longitud de la parte superior, no puede usar este método.

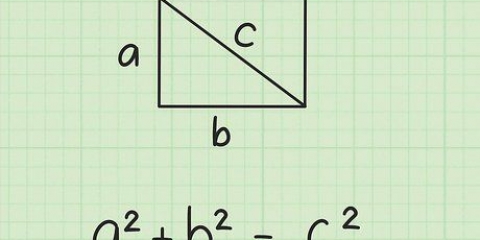
4. Establezca el teorema de Pitágoras para el primer triángulo rectángulo. la fórmula es  , por lo cual
, por lo cual  es la longitud de la hipotenusa del triángulo rectángulo (el lado opuesto al ángulo recto),
es la longitud de la hipotenusa del triángulo rectángulo (el lado opuesto al ángulo recto),  es la altura del triángulo rectángulo y
es la altura del triángulo rectángulo y  es la longitud de la base del triangulo.
es la longitud de la base del triangulo.
 , por lo cual
, por lo cual  es la longitud de la hipotenusa del triángulo rectángulo (el lado opuesto al ángulo recto),
es la longitud de la hipotenusa del triángulo rectángulo (el lado opuesto al ángulo recto),  es la altura del triángulo rectángulo y
es la altura del triángulo rectángulo y  es la longitud de la base del triangulo.
es la longitud de la base del triangulo.
5. Usa los valores conocidos del primer triángulo en la fórmula. Asegúrese de ingresar la longitud del lado del trapezoide para  . Introduzca la altura del trapezoide para
. Introduzca la altura del trapezoide para  .
.
 . Introduzca la altura del trapezoide para
. Introduzca la altura del trapezoide para  .
.

6. Cuadrar los valores conocidos en la ecuación. Luego resta los valores al cuadrado entre sí para obtener  aislar.
aislar.
 aislar.
aislar. , luego elevas al cuadrado 6 y 9, y restas el cuadrado de 6 al cuadrado de 9:
, luego elevas al cuadrado 6 y 9, y restas el cuadrado de 6 al cuadrado de 9:



7. Saca la raíz cuadrada para obtener el valor de B  encontrar. (Para obtener instrucciones completas sobre cómo simplificar raíces cuadradas, lea este artículo sobre el tema). El resultado te dará el valor de la base faltante de tu primer triángulo rectángulo. Escribe esta longitud en la base de tu triángulo.
encontrar. (Para obtener instrucciones completas sobre cómo simplificar raíces cuadradas, lea este artículo sobre el tema). El resultado te dará el valor de la base faltante de tu primer triángulo rectángulo. Escribe esta longitud en la base de tu triángulo.
 encontrar. (Para obtener instrucciones completas sobre cómo simplificar raíces cuadradas, lea este artículo sobre el tema). El resultado te dará el valor de la base faltante de tu primer triángulo rectángulo. Escribe esta longitud en la base de tu triángulo.
encontrar. (Para obtener instrucciones completas sobre cómo simplificar raíces cuadradas, lea este artículo sobre el tema). El resultado te dará el valor de la base faltante de tu primer triángulo rectángulo. Escribe esta longitud en la base de tu triángulo.



Así que toma nota
 como base del primer triangulo.
como base del primer triangulo.
8. Encuentra la longitud faltante del segundo triángulo rectángulo. Para hacer esto, establezca el teorema de Pitágoras para el segundo triángulo y siga los pasos para encontrar la longitud del lado que falta. Si estás trabajando con un trapezoide isósceles (aquel en el que los dos lados no paralelos tienen la misma longitud), entonces los dos triángulos rectángulos son congruentes, por lo que el valor del primer triángulo es igual al del segundo triángulo.





Así que toma nota
 como la base del segundo triangulo.
como la base del segundo triangulo.
9. Suma todas las longitudes de los lados del trapezoide. El perímetro de cualquier polígono es la suma de todos sus lados:  . Para la parte inferior, agregue el lado inferior del rectángulo, más las bases de los dos triángulos. Probablemente tendrás raíces cuadradas en tu respuesta. Para obtener instrucciones completas sobre cómo sumar raíces cuadradas, lea el artículo sobre este tema. También puedes usar una calculadora para convertir las raíces cuadradas a decimales.
. Para la parte inferior, agregue el lado inferior del rectángulo, más las bases de los dos triángulos. Probablemente tendrás raíces cuadradas en tu respuesta. Para obtener instrucciones completas sobre cómo sumar raíces cuadradas, lea el artículo sobre este tema. También puedes usar una calculadora para convertir las raíces cuadradas a decimales.
 . Para la parte inferior, agregue el lado inferior del rectángulo, más las bases de los dos triángulos. Probablemente tendrás raíces cuadradas en tu respuesta. Para obtener instrucciones completas sobre cómo sumar raíces cuadradas, lea el artículo sobre este tema. También puedes usar una calculadora para convertir las raíces cuadradas a decimales.
. Para la parte inferior, agregue el lado inferior del rectángulo, más las bases de los dos triángulos. Probablemente tendrás raíces cuadradas en tu respuesta. Para obtener instrucciones completas sobre cómo sumar raíces cuadradas, lea el artículo sobre este tema. También puedes usar una calculadora para convertir las raíces cuadradas a decimales.
Después de convertir las raíces cuadradas a decimales, tienes

Entonces, la circunferencia aproximada de tu trapezoide es 38.314 cm..
Método 3 de 3: si conoce la altura, la longitud de las esquinas internas superior e inferior

1. Divide el trapezoide en un rectángulo y dos triángulos rectángulos. Para esto, indique la altura desde ambas esquinas superiores.
- Si no puedes formar dos triángulos rectángulos porque un lado del trapecio es perpendicular a la base, asegúrate de que este lado tenga el mismo tamaño que la altura y divide el trapezoide en un rectángulo y un triángulo rectángulo.

2. Etiqueta cada contorno. Como estos son lados opuestos de un rectángulo, tendrán la misma longitud.

3. Tenga en cuenta la longitud de la parte media de la parte inferior. (Esta es la parte inferior del rectángulo.) Esta longitud será igual a la longitud de la parte superior, porque los lados opuestos de un rectángulo tienen la misma longitud.

4. Establece la fórmula del seno para el primer triángulo rectángulo. la fórmula es  , por lo cual
, por lo cual  la esquina interior es,
la esquina interior es,  la altura del triangulo y
la altura del triangulo y  es la longitud de la hipotenusa.
es la longitud de la hipotenusa.
 , por lo cual
, por lo cual  la esquina interior es,
la esquina interior es,  la altura del triangulo y
la altura del triangulo y  es la longitud de la hipotenusa.
es la longitud de la hipotenusa.
5. Usa los valores conocidos en la relación del seno. Asegúrate de usar la altura del triángulo como la longitud del lado opuesto en la fórmula. resuelves esto para H.


6. Determinar el seno del ángulo. Haz esto usando el botón SIN en una calculadora científica. Utilice este valor en la fórmula.


7. Resuelva esto para H. Para hacer esto, multiplique cada lado por H, luego divida cada lado por el ángulo del seno. O divide la altura del triángulo por el ángulo del seno.




Por lo tanto, la longitud de la hipotenusa y el primer lado faltante del trapecio es de aproximadamente 10,4566 cm.

8. Encuentre la longitud de la hipotenusa del segundo triángulo rectángulo. Establezca la fórmula del seno ( ) para el segundo ángulo interior dado. Esto te dará la longitud de la hipotenusa, que también es el primer lado del trapezoide.
) para el segundo ángulo interior dado. Esto te dará la longitud de la hipotenusa, que también es el primer lado del trapezoide.
 ) para el segundo ángulo interior dado. Esto te dará la longitud de la hipotenusa, que también es el primer lado del trapezoide.
) para el segundo ángulo interior dado. Esto te dará la longitud de la hipotenusa, que también es el primer lado del trapezoide.




Entonces, la longitud de la hipotenusa y el segundo lado faltante del trapezoide es de aproximadamente 8,4854 cm.

9. Establezca el teorema de Pitágoras para el primer triángulo rectángulo. El teorema de Pitágoras es ruidoso  , donde la longitud de la hipotenusa es igual a
, donde la longitud de la hipotenusa es igual a  , y la altura del triangulo
, y la altura del triangulo  .
.
 , donde la longitud de la hipotenusa es igual a
, donde la longitud de la hipotenusa es igual a  , y la altura del triangulo
, y la altura del triangulo  .
.
10. Usa los valores conocidos en el teorema de Pitágoras para el primer triángulo rectángulo. Asegúrese de ingresar el valor correcto para la hipotenusa  y la altura
y la altura  .
.
 y la altura
y la altura  .
.

11. Resuelve esto para B  . Esto te dará la longitud de la base del primer triángulo rectángulo y la primera parte faltante de la base del trapezoide.
. Esto te dará la longitud de la base del primer triángulo rectángulo y la primera parte faltante de la base del trapezoide.
 . Esto te dará la longitud de la base del primer triángulo rectángulo y la primera parte faltante de la base del trapezoide.
. Esto te dará la longitud de la base del primer triángulo rectángulo y la primera parte faltante de la base del trapezoide.





Entonces, la base del triángulo y la primera parte que falta en la parte inferior del trapezoide mide aproximadamente 8,5639 cm.

12. Encuentra la longitud de la base faltante del segundo triángulo rectángulo. Utilice el teorema de Pitágoras ( ). Usa la longitud de la hipotenusa para
). Usa la longitud de la hipotenusa para  y la altura para
y la altura para  . Resuelve esto para
. Resuelve esto para  y obtienes la longitud de la segunda parte faltante de la parte inferior del trapezoide.
y obtienes la longitud de la segunda parte faltante de la parte inferior del trapezoide.
 ). Usa la longitud de la hipotenusa para
). Usa la longitud de la hipotenusa para  y la altura para
y la altura para  . Resuelve esto para
. Resuelve esto para  y obtienes la longitud de la segunda parte faltante de la parte inferior del trapezoide.
y obtienes la longitud de la segunda parte faltante de la parte inferior del trapezoide.





Entonces, la base del segundo triángulo y la segunda parte que falta en la parte inferior del trapezoide es igual a 6 cm.

13. Suma todos los lados del trapezoide. El perímetro de cualquier polígono es la suma de todos sus lados:  . Para la parte inferior, agregue la parte inferior del rectángulo a la base de los dos triángulos.
. Para la parte inferior, agregue la parte inferior del rectángulo a la base de los dos triángulos.
 . Para la parte inferior, agregue la parte inferior del rectángulo a la base de los dos triángulos.
. Para la parte inferior, agregue la parte inferior del rectángulo a la base de los dos triángulos.
Entonces la circunferencia aproximada del trapezoide es 45.5059 cm.
Consejos
- Usa las leyes de los triángulos especiales para encontrar las longitudes faltantes de los triángulos especiales, sin usar la fórmula del seno o el teorema de Pitágoras. Las leyes se aplican a un triángulo 30-60-90 o a un triángulo 90-45-45.
- Use una calculadora científica para determinar el seno de un ángulo, ingresando el ángulo y luego presionando el botón `SIN`. También puedes usar una tabla de trigonometría.
Artículos de primera necesidad
- Calculadora
- Lápiz
- Papel
Artículos sobre el tema. "Calcular el perímetro de un trapezoide"
Оцените, пожалуйста статью
Popular