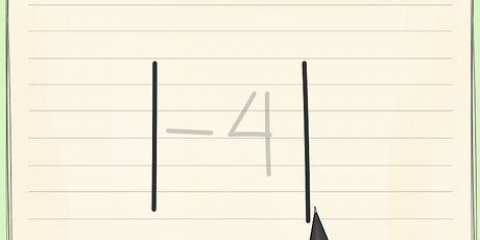
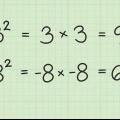En este ejemplo, el primer conjunto de tres números multiplicados juntos es igual a 10. Determinar el cubo más grande que es menor que 10. eso es 8 y su raiz cubica es 2. Escribe el número 2 arriba del signo radical, arriba del número 10. Anota el valor de  , igual a 8, debajo del número 10; dibujar una línea y restar los números de la misma manera que en la división larga. el resultado es 2.
, igual a 8, debajo del número 10; dibujar una línea y restar los números de la misma manera que en la división larga. el resultado es 2. Después de esta suma menos tienes el primer dígito de tu respuesta. Tendrás que comprobar si este número es lo suficientemente exacto. En la mayoría de los casos, este no será el caso. Puede verificar esto elevando el número al cubo y viendo si está lo suficientemente cerca del resultado deseado. En este caso  es igual a 8, y eso no está muy cerca de 10, así que tienes que seguir adelante.
es igual a 8, y eso no está muy cerca de 10, así que tienes que seguir adelante. 
A la izquierda de la línea vertical, escribe la solución del próximo divisor, como la suma de tres números separados. Indique los espacios en blanco para estos números subrayando tres espacios en blanco con signos más debajo de ellos. 


Ahora calcula 3 veces 10 veces cada uno de los dos números que existen en tu solución arriba del radical. Para este problema simple, eso significa 3*10*2*1, que es igual a 60. Agrega esto a los 1200 que ya tenías y obtienes 1260. Finalmente, suma el cuadrado del último dígito. En este ejemplo, eso es 1; y 1^2 sigue siendo 1. Entonces el divisor total es 1200+60+1, o 1261. Tenga en cuenta esto a la izquierda de la línea vertical. 

Puedes verificar la precisión de este resultado usando el cubo: 2.1*2.1*2.1. El resultado es 9,261. Si cree que el resultado es lo suficientemente exacto, puede dejar de. Si quieres una respuesta más exacta, tienes que pasar por otra ronda. 
Tome el siguiente grupo de tres números hacia abajo. En este caso se trata de tres ceros, que vienen después del resto 739 y por lo tanto 739.000 formas. Comience el divisor en 300 veces el cuadrado del número actualmente arriba del radical. Esto es  , y por lo tanto 132.300.
, y por lo tanto 132.300. Seleccione el siguiente dígito de su solución para que pueda multiplicarlo por 132.300 y menos del 739.000 de tu resto. Una buena opción sería 5, porque 5*132.300=661.500. Escribe el número 5 en el siguiente espacio arriba de la línea radical. Encuentra 3 veces el número anterior sobre la línea radical, 21, multiplicado por el último dígito que acabas de escribir, 5, multiplicado por 10. Esto da  .
. Finalmente, elevas al cuadrado el último dígito. Esto es 
Suma los términos de tu divisor y obtienes 132.300+3150+25=135.475. 
Multiplica el divisor por el último dígito de tu solución. 135.475*5=677.375. sustraer. 739.000-677.375=61.625. Considere si la solución 2.15 es lo suficientemente exacta. Calcula su cubo y obtienes  .
. 


En el problema de ejemplo, 600 (su número objetivo) cae aproximadamente a la mitad entre los números límite 512 y 729. Así que elige tu 5 como tu próximo número. 
En este ejemplo, se multiplica 

Por ejemplo, en este problema,  más grande que el objetivo (600). Entonces reduce la estimación a 8.4. Tome el cubo de este número y compárelo con su objetivo. verás que
más grande que el objetivo (600). Entonces reduce la estimación a 8.4. Tome el cubo de este número y compárelo con su objetivo. verás que  . Esto ahora es más bajo que su objetivo. Esto te dice que la raíz cúbica de 600 debe ser al menos 8,4, pero menor que 8,5.
. Esto ahora es más bajo que su objetivo. Esto te dice que la raíz cúbica de 600 debe ser al menos 8,4, pero menor que 8,5. 
En este problema de ejemplo, su última ronda de cálculos muestra que  , mientras
, mientras  . El objetivo (600) está ligeramente más cerca de 592 que de 614. Entonces, ¿estima el siguiente número un poco menos de la mitad entre 0 y 9?. Una buena elección es 4, que te dará una estimación de la raíz cúbica de 8,44.
. El objetivo (600) está ligeramente más cerca de 592 que de 614. Entonces, ¿estima el siguiente número un poco menos de la mitad entre 0 y 9?. Una buena elección es 4, que te dará una estimación de la raíz cúbica de 8,44. 
Para este problema de ejemplo, comience observando que  . Esto está justo por encima del objetivo, así que suelte un poco y pruebe 8.43. Esto da
. Esto está justo por encima del objetivo, así que suelte un poco y pruebe 8.43. Esto da  como resultado. Entonces sabes que la raíz cúbica de 600 es un poco más de 8.43 y un poco menos de 8.44.
como resultado. Entonces sabes que la raíz cúbica de 600 es un poco más de 8.43 y un poco menos de 8.44. 
Para el ejemplo de la raíz cúbica de 600, suponiendo dos números decimales, 8,43 está a menos de 1 del número objetivo. Si continúa con tres dígitos después del punto decimal, verá que  si el resultado es 0.1 menos que la respuesta real.
si el resultado es 0.1 menos que la respuesta real. 

Para obtener más información sobre el binomio de Newton y obtener este resultado, lea más sobre la multiplicación de binomios en wikiHow. Si desea una versión más profunda y rápida, lea más sobre el Triángulo de Pascal. 

El primer término contiene un plural de 1000. Primero elige un número que podría elevarse al cubo y permanecer dentro del rango de división larga como el primer dígito. Esto produce el término 1000A^3 en el binomio. El segundo término del binomio de Newton tiene un coeficiente de 300. (Esto es de  .) Recuerda que al calcular la raíz cúbica, el primer dígito de cada paso se multiplicó por 0300.
.) Recuerda que al calcular la raíz cúbica, el primer dígito de cada paso se multiplicó por 0300. El segundo dígito en cada paso del cálculo de la raíz cúbica proviene del tercer término del binomio de Newton. En el binomio de Newton ves el término 30AB^2. El último dígito de cada paso es el término B^3. 
Calcular raíces cúbicas a mano
Contenido
Usando una calculadora, calcular la raíz cúbica de cualquier número es solo presionar algunas teclas. Pero tal vez no tengas una calculadora o quieras impresionar a tus amigos con tu habilidad para calcular una raíz cúbica de forma improvisada. Hay un método que parece un poco difícil a primera vista, pero funciona muy fácilmente con un poco de práctica. Es útil tener algunos conocimientos en el campo de las habilidades aritméticas y el cálculo de números cúbicos.
Pasos
Parte 1 de 3: Elaborar una tarea de muestra

1. preparar la tarea. Resolver la raíz cúbica de un número se verá como resolver una división larga, con algunas diferencias aquí y allá. El primer paso es escribir el problema correctamente.
- Escribe el número del que quieres encontrar la raíz cúbica. Escribe los números en grupos de tres, donde la coma es el punto de partida. En este ejemplo vas a encontrar la raíz cúbica de 10. Escriba esto como 10,000000. Los ceros son necesarios para la precisión de la respuesta.
- Dibujar un radical del cubo sobre el número. Esto tiene el mismo propósito que la línea de división larga. La única diferencia es la forma del símbolo.
- Coloque una coma encima de la línea, directamente encima del punto decimal en el número original.

2. Conoce los cubos de las unidades. Usarás esto en tus cálculos. Se trata de las siguientes terceras potencias:











3. Encuentra el primer dígito de tu respuesta. Seleccione un número que, al cubo, dé el mayor resultado posible que sea menor que el primer conjunto de tres números.
 , igual a 8, debajo del número 10; dibujar una línea y restar los números de la misma manera que en la división larga. el resultado es 2.
, igual a 8, debajo del número 10; dibujar una línea y restar los números de la misma manera que en la división larga. el resultado es 2. es igual a 8, y eso no está muy cerca de 10, así que tienes que seguir adelante.
es igual a 8, y eso no está muy cerca de 10, así que tienes que seguir adelante.
4. Hacer la alineación para el siguiente dígito. Escriba el siguiente grupo de tres números en el resto y dibuje una línea vertical corta a la izquierda del número resultante. Este será el número que usaremos para determinar el siguiente dígito en su solución de raíz cúbica. En este ejemplo, será 2000, que se crea a partir del resto 2 de la suma menos anterior, con el grupo de tres ceros que eliminaste.

5. Encuentra el comienzo del siguiente divisor. Para la primera parte del divisor, escribe trescientas veces el cuadrado de lo que está arriba del radical. En este caso, eso es 2; 2^2 es 4, y 4*300=1200. Entonces escribe 1200 en el primer espacio vacío. El divisor para este paso de la solución será 1200, más algo más que estarás calculando en un minuto.

6. Encuentra el siguiente número en tu raíz cúbica. Encuentre el siguiente dígito de su solución seleccionando lo que puede multiplicar por el divisor (1200 y algo), luego reste del resto de 2000. Esto solo puede ser 1, porque 2 por 1200 es igual a 2400, que es mayor que 2000. Escribe el número 1 en el siguiente espacio arriba del radical.

7. Encuentra el resto del divisor. El divisor en este paso de la solución consta de tres partes. La primera parte es la 1200 que ya tienes. Ahora deberá agregar dos términos adicionales para completar el divisor.

8. Multiplicar y restar. Redondea esta parte de la solución multiplicando el último dígito de tu solución, en este caso el número 1, por el divisor que acabas de calcular (1261). 1*1261 =1261. Escribe esto debajo de 2000 y réstale 1261 para obtener 739.

9. Decide que debes ir más lejos para obtener una respuesta más precisa. Después de completar la suma menos de cada paso, debe verificar si su respuesta es lo suficientemente exacta. Para la raíz cúbica de 10: después de la primera suma menos, la raíz cúbica era solo 2, y eso no es realmente exacto. Ahora, después de la segunda ronda, la solución es 2.1.

10. Determinar el crupier para la siguiente ronda. En este caso, para más práctica y una respuesta más precisa, repite los pasos para otra ronda, de la siguiente manera:
 , y por lo tanto 132.300.
, y por lo tanto 132.300. .
.

11. Multiplica el divisor por el resultado. Después de calcular el divisor en esta próxima ronda y expandir tu solución en un dígito más, procede de la siguiente manera:
 .
.
12. Anota tu respuesta final. El resultado sobre el radical es la raíz cúbica, con una precisión de tres dígitos significativos. En este ejemplo, la raíz cúbica de 10 es igual a 2,15. Verifique esto calculando 2.15^3=9.94 que se puede redondear a 10. Si necesita una respuesta más precisa, continúe hasta que esté satisfecho.
Parte 2 de 3: Hallar la raíz cúbica a través de estimaciones repetidas

1. Use números cúbicos para establecer los límites superior e inferior. Cuando se le solicite una raíz cúbica de un número determinado, comience eligiendo un cubo que esté lo más cerca posible de él, sin ser mayor que su número objetivo.
- Por ejemplo, si quieres encontrar la raíz cúbica de 600, recuerda (o usa una tabla de cubos) que
y
. Por lo tanto, la solución a la raíz cúbica de 600 será algo entre 8 y 9. Usa los números 512 y 729 como límites superior e inferior para tu solución.

2. Adivinar el siguiente número. Sabías el primer dígito debido a tu conocimiento de ciertos números cúbicos. Para el siguiente dígito, calcule un número entre 0 y 9 en función de dónde se encuentra su número objetivo entre los dos números límite.

3. Pon a prueba tu conjetura determinando su cubo. Intente multiplicar la estimación con la que está trabajando ahora para ver qué tan cerca está del número objetivo.


4. Ajuste su estimación cuando sea necesario. Después de subir al cubo de tu última suposición, compara el resultado con tu número objetivo. Si el resultado es mayor que el objetivo, su estimación debe ser menor. Si el resultado es menor que la meta, hay que ajustarlo hacia arriba hasta llegar a la meta.
 más grande que el objetivo (600). Entonces reduce la estimación a 8.4. Tome el cubo de este número y compárelo con su objetivo. verás que
más grande que el objetivo (600). Entonces reduce la estimación a 8.4. Tome el cubo de este número y compárelo con su objetivo. verás que  . Esto ahora es más bajo que su objetivo. Esto te dice que la raíz cúbica de 600 debe ser al menos 8,4, pero menor que 8,5.
. Esto ahora es más bajo que su objetivo. Esto te dice que la raíz cúbica de 600 debe ser al menos 8,4, pero menor que 8,5.
5. Estime el siguiente número para obtener una respuesta más precisa. Continúe con este procedimiento de estimación de números del 0 al 9, hasta que su respuesta sea tan precisa como desea que sea. Para cada ronda de estimación, comience por verificar la posición de su último cálculo entre los números límite.
 , mientras
, mientras  . El objetivo (600) está ligeramente más cerca de 592 que de 614. Entonces, ¿estima el siguiente número un poco menos de la mitad entre 0 y 9?. Una buena elección es 4, que te dará una estimación de la raíz cúbica de 8,44.
. El objetivo (600) está ligeramente más cerca de 592 que de 614. Entonces, ¿estima el siguiente número un poco menos de la mitad entre 0 y 9?. Una buena elección es 4, que te dará una estimación de la raíz cúbica de 8,44.
6. Continúe estimando y ajustando Haga esto tantas veces como sea necesario, eleve su estimación al cubo y vea cómo se compara con el número objetivo. Busque números que estén justo debajo o justo encima del número objetivo.
 . Esto está justo por encima del objetivo, así que suelte un poco y pruebe 8.43. Esto da
. Esto está justo por encima del objetivo, así que suelte un poco y pruebe 8.43. Esto da  como resultado. Entonces sabes que la raíz cúbica de 600 es un poco más de 8.43 y un poco menos de 8.44.
como resultado. Entonces sabes que la raíz cúbica de 600 es un poco más de 8.43 y un poco menos de 8.44.
7. Continúe hasta que alcance la precisión deseada. Continúe estimando, comparando y reestimando, tanto tiempo como sea necesario, hasta que su solución sea tan precisa como desea que sea. Tenga en cuenta que con cada decimal, sus números objetivo se acercan cada vez más al número real.
 si el resultado es 0.1 menos que la respuesta real.
si el resultado es 0.1 menos que la respuesta real.Parte 3 de 3: Comprende cómo funciona este cálculo

1. Repase el binomio de Newton de nuevo. Para comprender por qué este algoritmo funciona para determinar las raíces cúbicas, primero debe pensar en cómo se ve el cubo como binomial. Probablemente aprendiste esto en matemáticas de la escuela secundaria (y como la mayoría de las personas, probablemente lo olvidaste bastante rápido). Seleccione dos variables  y
y  para representar unidades. Luego calculas el binomio de
para representar unidades. Luego calculas el binomio de  por las decenas.
por las decenas.
 y
y  para representar unidades. Luego calculas el binomio de
para representar unidades. Luego calculas el binomio de  por las decenas.
por las decenas. - Usa el término
para crear una docena. Cualquiera que sea el grado que seleccione para
,
formará una docena. Por ejemplo, si
es 2 y
es 6, entonces .se convierte en
igual a 26.

2. Escribe el binomio en un cubo. Ahora trabajamos al revés, primero determinando el cubo y luego viendo por qué funciona la solución de raíces cúbicas. Necesitamos los valores de  encontrar. Haces esto haciendo ejercicio
encontrar. Haces esto haciendo ejercicio  . Este es un cálculo demasiado largo para mostrarlo aquí, pero el resultado final es
. Este es un cálculo demasiado largo para mostrarlo aquí, pero el resultado final es  .
.
 encontrar. Haces esto haciendo ejercicio
encontrar. Haces esto haciendo ejercicio  . Este es un cálculo demasiado largo para mostrarlo aquí, pero el resultado final es
. Este es un cálculo demasiado largo para mostrarlo aquí, pero el resultado final es  .
.
3. Conoce el significado de la división larga. Tenga en cuenta que el método para calcular la raíz cúbica funciona como una división larga. En la división larga ves que dos factores se multiplican entre sí, da el número con el que empezaste. En este cálculo, el número que estás buscando (el número que termina arriba del radical) es la raíz cúbica. Eso significa que es igual al término (10A+B). Los A y B reales son irrelevantes ahora, siempre que comprenda la relación con la respuesta.

4. Ver la versión extendida. Cuando miras el binomio de Newton, ves por qué el algoritmo de raíz cúbica es correcto. Vea cómo el divisor en cada paso del algoritmo es igual a la suma de los cuatro términos que necesita calcular y sumar. Estos términos surgen de la siguiente manera:
 .) Recuerda que al calcular la raíz cúbica, el primer dígito de cada paso se multiplicó por 0300.
.) Recuerda que al calcular la raíz cúbica, el primer dígito de cada paso se multiplicó por 0300.
5. Vea cómo crece la precisión. Trabajando con divisiones largas, cada paso que completes le da una gran precisión a tu respuesta. Por ejemplo, el problema de ejemplo elaborado en este artículo es para determinar la raíz cúbica de 10. En el primer paso, la solución es 2, porque  se acerca, pero es menos de 10. De hecho,
se acerca, pero es menos de 10. De hecho,  . Después de la segunda ronda, tu solución es 2.1. Una vez que haya resuelto esto, obtendrá
. Después de la segunda ronda, tu solución es 2.1. Una vez que haya resuelto esto, obtendrá , y eso está mucho más cerca del resultado deseado (10). Después de la tercera ronda tienes 2,15, y eso te da
, y eso está mucho más cerca del resultado deseado (10). Después de la tercera ronda tienes 2,15, y eso te da  . Sigue trabajando en grupos de tres números y obtendrás una respuesta tan precisa como quieras.
. Sigue trabajando en grupos de tres números y obtendrás una respuesta tan precisa como quieras.
 se acerca, pero es menos de 10. De hecho,
se acerca, pero es menos de 10. De hecho,  . Después de la segunda ronda, tu solución es 2.1. Una vez que haya resuelto esto, obtendrá
. Después de la segunda ronda, tu solución es 2.1. Una vez que haya resuelto esto, obtendrá , y eso está mucho más cerca del resultado deseado (10). Después de la tercera ronda tienes 2,15, y eso te da
, y eso está mucho más cerca del resultado deseado (10). Después de la tercera ronda tienes 2,15, y eso te da  . Sigue trabajando en grupos de tres números y obtendrás una respuesta tan precisa como quieras.
. Sigue trabajando en grupos de tres números y obtendrás una respuesta tan precisa como quieras.Consejos
- Como todo, tus habilidades matemáticas mejorarán con la práctica. Cuanto más practiques, mejor podrás hacer este tipo de cálculos.
Advertencias
- Es fácil cometer un error aquí. Revise su trabajo cuidadosamente y vuelva a pasar por la elaboración.
Artículos de primera necesidad
- bolígrafo o lápiz
- Papel
- Gobernante
- Borrador
Artículos sobre el tema. "Calcular raíces cúbicas a mano"
Оцените, пожалуйста статью
Popular