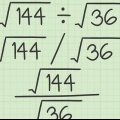Otro ejemplo: Queremos encontrar la raíz cuadrada de 25 (√(25)). Esto significa que necesitamos encontrar el número que multiplicado por sí mismo tiene como producto 25. Como 5 = 5 × 5 = 25, podemos decir que √(25) = 5. También puede pensar en esto como "deshacer" un cuadrado (o número de potencia). Por ejemplo, si queremos encontrar la raíz cuadrada de 64 (√64), considera 64 como 8. Primero. Dado que un radical en principio `elimina` un cuadrado, podemos decir que √(64) = √(8) = 8. 
Por otro lado, los números que no dan números enteros después de la raíz cuadrada se llaman, cuadrado imperfecto. Cuando sacas la raíz cuadrada de uno de estos números, por lo general obtienes un decimal o una fracción. A veces, los decimales involucrados pueden volverse realmente complicados. Por ejemplo, √(13) = 3.605551275464… 
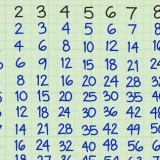
1 = 1 × 1 = 1 2 = 2 × 2 = 4 3 = 3 × 3 = 9 4 = 4 × 4 = dieciséis 5 = 5 × 5 = 25 6 = 6 × 6 = 36 7 = 7 × 7 = 49 8 = 8 × 8 = 64 9 = 9 × 9 = 81 10 = 10 × 10 = 100 11 = 11 × 11 = 121 12 = 12 × 12 = 144 
Supongamos que desea calcular la raíz cuadrada de 900. A primera vista esto parece muy difícil! Sin embargo, no es difícil si factorizamos 900. Los `factores` son aquellos números que pueden multiplicarse para formar otro número. Por ejemplo, dado que 6 es el producto de 1 × 6 y 2 × 3, los factores de 6 son los números 1, 2, 3 y 6. En lugar de calcular con el número 900, que es un poco inconveniente, lo escribimos como 9 × 100. Ahora, como 9 es un cuadrado perfecto y separado de 100, podemos sacar su raíz cuadrada. √(9 × 100) = √(9) × √(100) = 3 × √(100). En otras palabras, √(900) = 3√(100). Podemos simplificar estos dos pasos aún más dividiendo 100 en los factores 25 y 4. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Entonces podemos decir que √(900) = 3(10) = 30. 
Nota: Si bien los números imaginarios no se pueden representar con números regulares, aún se pueden tratar como números regulares de muchas maneras. Por ejemplo, las raíces de números negativos se pueden elevar al cuadrado para dar esos números negativos como cualquier otra raíz cuadrada. Por ejemplo: yo = -1. 

En nuestro ejemplo, dividimos 6.45 en pares como este: 6-,45-00. Tenga en cuenta que hay un número `restante` a la izquierda &mdash ese es el punto. 
En nuestro ejemplo, el primer grupo en 6-,45-00 es el 6. El mayor número menor o igual a 6 es 2 — 2 = 4. Escribe un `2` arriba del 6 debajo del radical. 
En nuestro ejemplo, comenzaremos con el doble de 2, el primer dígito de nuestra respuesta. 2 × 2 = 4. Luego restamos 4 de 6 (nuestro primer `grupo`) y obtenemos 2 como respuesta. Luego movemos el siguiente grupo (45) una línea hacia abajo para obtener 245. Finalmente, escribiremos otro 4 a la izquierda, dejando un pequeño espacio para agregar al final, así: 4_. 
En nuestro ejemplo, buscamos el número para llenar el espacio en blanco en 4_ × _; eso hace que la respuesta sea lo más grande posible, pero aún menor o igual a 245. En este caso la respuesta es 5. 45 × 5 = 225, mientras que 46 × 6 = 276. 
Seguimos con nuestro ejemplo y seguimos con 225 - 245 = 20. Luego bajamos el siguiente par de dígitos, 00, para hacer 2000. Si duplicamos el número sobre el radical, obtenemos 25 × 2 = 50. Resolvemos la incógnita en 50_ × _ =/< 2000, entonces obtenemos 3 como respuesta. En este punto tenemos `253` arriba del radical; repitiendo esto nuevamente, 9 es el siguiente dígito. 
En nuestro ejemplo, el número debajo del signo radical es 6.45, así que simplemente movemos el punto decimal hacia arriba y lo colocamos entre 2 y 5 de nuestra respuesta, lo que nos da 2,539 rendimientos. 

En nuestro problema de ejemplo, una estimación razonable para la raíz cuadrada de 40 es tal vez 6.4, porque de lo anterior sabemos que la respuesta probablemente esté un poco más cerca de 6 que de 7. 
Multiplica 6,4 por sí mismo, entonces 6,4 × 6,4 = 40.96, que es un poco más grande que el número original. Luego multiplicamos el número por una décima más pequeña que nuestra estimación anterior (porque nuestra respuesta fue demasiado alta) y obtenemos 6,3 × 6,3 = 39.69. Esto es ligeramente más bajo que nuestro número original. Esto significa que la raíz cuadrada de 40 está en algún lugar entre 6,3 y 6,4 mentiras. Además, como 39,69 está más cerca de 40 que de 40,96, sabes que la raíz cuadrada está más cerca de 6,3 que de 6,4. 
En nuestro ejemplo, elijamos 6,33 para nuestra suposición con dos decimales. Cuadra 6.33 y obtienes 6.33 × 6.33 = 40.0689. Dado que está ligeramente por encima de nuestro número original, intentaremos con un número ligeramente más bajo, como 6,32. 6,32 × 6,32 = 39,9424. Esto está ligeramente por debajo de nuestro número original, por lo que sabemos que la raíz cuadrada exacta entre 6.33 y 6.32 mentiras. Si quisiéramos ir más allá, podemos continuar usando el mismo enfoque para obtener una respuesta cada vez más precisa.
Resolver raíces cuadradas
Contenido
Si bien la vista intimidante de un símbolo de raíz cuadrada puede hacer que las personas con ansiedad matemática se estremezcan, los problemas de raíz cuadrada no son tan difíciles de resolver como parecen a primera vista. Los problemas simples de raíces cuadradas a menudo se pueden resolver tan fácilmente como los problemas simples de multiplicación y división. Los problemas de raíces cuadradas más complejos, por otro lado, pueden requerir un poco más de trabajo, pero con el enfoque correcto, incluso estos problemas se pueden resolver fácilmente. Comience a practicar problemas de raíces cuadradas hoy para aprender esta habilidad matemática que puede ser nueva para usted!
Pasos
Parte 1 de 3: Comprender los poderes y las raíces

1. Cuadrar un número multiplicándolo por sí mismo. Para entender las raíces, lo mejor es empezar con los cuadrados. Los cuadrados son fáciles: elevar un número al cuadrado equivale a multiplicarlo por sí mismo. Por ejemplo: 3 al cuadrado es lo mismo que 3 × 3 = 9, y 9 al cuadrado es lo mismo que 9 × 9 = 81. Los cuadrados se indican con un pequeño "2" arriba y a la derecha del número al cuadrado, así: 3, 9, 100, etc.
- Intente elevar algunos números al cuadrado para probar este concepto. Recuerda que elevar un número al cuadrado no es más que multiplicar ese número por sí mismo. Puedes hacer esto incluso con números negativos. En todos los casos, la respuesta siempre será positiva. Por ejemplo: -8 = -8 × -8 = 64.

2. Para encontrar la raíz de un número, encuentra el `inverso de` un cuadrado. El símbolo de la raíz cuadrada (√, también conocido como el `signo radical`) es básicamente el `opuesto` del símbolo del cuadrado (). Si ves un signo radical, puedes preguntarte: `¿Qué número puedo multiplicar por sí mismo para obtener el número debajo del signo radical??` Por ejemplo: si ves la raíz cuadrada √(9), entonces estás buscando el número que multiplicado por sí mismo tiene nueve como producto. En este caso eso es Tres, porque 3 = 9.

3. Conoce la diferencia entre cuadrados perfectos e imperfectos. Hasta ahora, las respuestas a los problemas de raíces cuadradas eran agradables, números redondos. Este no siempre es el caso; de hecho, hay respuestas a las raíces cuadradas que son números decimales muy largos e incómodos. Los números raíces que son números enteros (en otras palabras, números que no son fracciones o decimales) se llaman cuadrícula. Todos los ejemplos anteriores (9, 25 y 64) son cuadrados (también llamados cuadrados perfectos), porque al sacar raíces cuadradas, obtenemos números enteros (3, 5 y 8) como resultado.

4. Memoriza los primeros 10-12 cuadrados. Como probablemente habrás notado, las raíces cuadradas o los cuadrados suelen ser muy fáciles! Debido a que estos problemas matemáticos son tan simples, vale la pena dedicar tiempo a aprender las raíces de los primeros 12 o más cuadrados. Encontrará estos números con mucha frecuencia, por lo que puede ahorrar mucho tiempo a largo plazo si los aprende temprano. Los primeros 12 cuadrados son:

5. Simplifique las raíces eliminando cuadrados donde sea posible. Encontrar las raíces de los cuadrados imperfectos a veces puede ser complicado, especialmente si no usa una calculadora (los párrafos a continuación le brindan trucos para facilitar este proceso). Sin embargo, a menudo es posible simplificar los números bajo el signo radical, para facilitar el trabajo con ellos. Para hacer esto, solo necesita factorizar el número debajo del radical, luego sacar la raíz cuadrada de los factores que son cuadrados y escribir la respuesta fuera del radical. Esto es más fácil de lo que parece: sigue leyendo para obtener más información!

6. Usar números imaginarios para las raíces de números negativos. ¿Qué cuadrado es -16?? No es 4 o -4: elevar ambos al cuadrado da 16 (positivo). No lo sabes? De hecho, no hay forma de escribir la raíz cuadrada de -16 o cualquier número negativo con números regulares. En estos casos necesitamos usar números imaginarios (generalmente en forma de letras o símbolos) para reemplazar la raíz cuadrada del número negativo. Por ejemplo, la variable `i` generalmente se usa para la raíz cuadrada de -1. Como regla general, la raíz cuadrada de un número negativo siempre será un número imaginario (o contendrá uno).
Parte 2 de 3: usar algoritmos de división larga

1. Ordena tu problema de raíz cuadrada como una división larga. Aunque puede llevar un poco de tiempo, es posible calcular las raíces de cuadrados imperfectos difíciles sin una calculadora. Para hacer esto, usamos un método de solución (o algoritmo) que es similar a — pero no exactamente igual a — una división larga.
- Primero escriba la raíz cuadrada de la misma manera que la división larga. Por ejemplo, digamos que queremos calcular la raíz cuadrada de 6.45, que ciertamente no es un cuadrado perfecto conveniente. Primero escribimos un símbolo radical ordinario (√), luego escribimos el número debajo. Luego dibujamos una línea sobre el número, por lo que está en un pequeño `recuadro`, al igual que la división larga. Cuando terminamos, notamos un `√` alargado con 6.45 debajo.
- Escribimos números arriba del problema, así que deja algo de espacio.

2. Agrupa los números en pares. Para resolver tu problema, agrupa los dígitos del número bajo el signo radical en pares, comenzando desde el punto decimal. Puede agregar pequeños puntos destacados (como puntos, barras, comas, etc.).) entre tus pares para distinguirlos.

3. Encuentre el número más grande cuyo cuadrado sea menor o igual que el primer `grupo`. Comience con el primer número o par a la izquierda. Elija el número más grande con un cuadrado que sea menor o igual que el `grupo`. Por ejemplo, si el grupo es 37, elegiría el 6, porque 6 = 36 (menor que 37), pero 7 = 49 (mayor que 37). Escribe este número encima del primer grupo. Este es el primer dígito de tu respuesta.

4. Duplica el número que acabas de escribir, escríbelo debajo del primer grupo y réstalo. Toma el primer dígito de tu respuesta (el número que acabas de encontrar) y duplícalo. Escribe esto debajo de tu primer grupo y réstalo para encontrar la diferencia. Coloque el siguiente par de números al lado de la respuesta a continuación. Finalmente, escribe el último dígito del doble del primer dígito de tu respuesta a la izquierda, dejando un espacio al lado.

5. Llena el espacio vacío. A continuación, la intención es añadir un dígito a la derecha del número que has escrito a la izquierda. Elija un número que multiplicado por su nuevo número produzca el mayor producto posible, pero que sea menor o igual que el número "retirado". Por ejemplo, si su número `retirado` es 1700 y el número de la izquierda es 40_, debe completar el espacio en blanco con `404` porque 404 × 4 = 1616 (menos de 1700), mientras que 405 × 5 = 2025. El número que encuentre en este paso es el segundo dígito de su respuesta, por lo que puede agregarlo arriba del radical.

6. Continúe usando sus números `en blanco` para su respuesta. Continúe con esta división larga modificada hasta que obtenga ceros cuando reste el número de `reducción`, o haya alcanzado la precisión deseada. Cuando termines, los números que usaste para llenar los espacios en blanco en cada paso (más el primer número que usaste) son los dígitos de tu respuesta.

7. Mueva el punto decimal de su `divisor` original hacia arriba. Para redondear su respuesta, debe colocar la coma (el punto decimal) en el lugar correcto. Afortunadamente, esto es fácil: todo lo que tiene que hacer es alinearlo con el punto decimal en su número original. Si el número debajo del radical es 49.8, mueva el punto decimal hacia arriba entre los dos números arriba de 9 y 8.
Parte 3 de 3: Estimar cuadrados imperfectos rápidamente

1. Encuentra cuadrados imperfectos estimando. Una vez que hayas memorizado tus cuadrados, encontrar las raíces de los cuadrados imperfectos se vuelve mucho más fácil. Como ya conoces una docena de cuadrados, cualquier número que se encuentre entre dos de estos cuadrados perfectos se puede encontrar estimando entre estos valores. Para empezar, encuentra los dos cuadrados entre los que cae tu número. Luego determina cuál de estos dos cuadrados está más cerca del número.
- Por ejemplo, supongamos que necesitamos encontrar la raíz cuadrada de 40. Como hemos memorizado nuestros cuadrados, podemos decir que 40 cae entre 6 y 7, o 36 y 49. Como 40 es mayor que 6, su raíz cuadrada será mayor que 6, y como es menor que 7, su raíz cuadrada será menor que 7. El número 40 está un poco más cerca del 36 que del 49, por lo que la respuesta probablemente estará un poco más cerca del 6. En los próximos pasos haremos que nuestra respuesta sea más precisa.

2. Estimar la raíz cuadrada con un decimal. Una vez que haya elegido dos cuadrados entre los cuales se encuentra su número, solo es cuestión de estimar hasta que encuentre una respuesta con la que esté satisfecho. Cuanto más avanzas, más precisa es tu respuesta. Para comenzar, elija un diez para su respuesta; no tiene que ser correcto, pero ahorrará tiempo si usa el sentido común al elegir un número que se acerque a la respuesta correcta.

3. Multiplica la estimación por sí misma. Luego elevas al cuadrado la estimación. A menos que tenga suerte, probablemente no obtendrá su número original; terminará ligeramente más alto o más bajo. Si su respuesta es demasiado alta, vuelva a intentarlo con una estimación un poco más pequeña (y viceversa si es demasiado baja).

4. Continúe estimando si es necesario. Si está satisfecho con sus respuestas, es posible que desee usar una de sus primeras conjeturas. Sin embargo, si desea una respuesta más precisa, todo lo que necesita hacer es elegir una estimación para su "centésima" que coloque esta estimación entre sus dos primeros. Si continúa con este patrón, puede obtener una respuesta con tres, cuatro o más decimales; solo depende de qué tan lejos quiera llegar.
Consejos
- Para soluciones rápidas, use una calculadora. La mayoría de las calculadoras modernas pueden calcular raíces cuadradas directamente. Por lo general, solo necesita ingresar su número y luego presionar el botón con el radical de la segunda potencia (la raíz cuadrada). Por ejemplo, para encontrar la raíz cuadrada de 841, presiona las siguientes teclas: 8, 4, 1, (√) y acierta 29 en como respuesta.
Artículos sobre el tema. "Resolver raíces cuadradas"
Оцените, пожалуйста статью
Popular