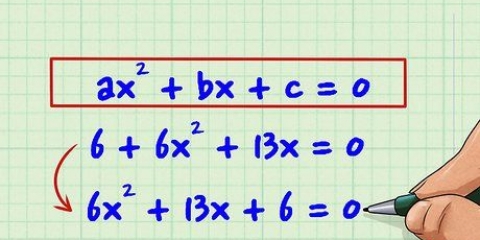4x = 8 - 2y (4x)/4 = (8/4) - (2y/4) x = 2 - y 
Ahora sabes que: x = 2 - y. La segunda ecuación, que aún no has cambiado, es: 5x + 3x = 9. En la segunda ecuación, reemplaza x con `2 - ½y`: 5(2 - ½y) + 3y = 9. 
5(2 - ½y) + 3y = 9 10 – (5/2)y + 3y = 9 10 – (5/2) y + (6/2) y = 9 (Si no entiende este paso, aprenda como sumar fracciones. Esto es a menudo, pero no siempre, necesario con este método). 10 + y = 9 y = -1 y = -2 
Ahora sabes que: y = -2 Una de las ecuaciones originales es: 4x + 2y = 8. (Ambas ecuaciones se pueden usar para este paso). Introduce -2 en lugar de y: 4x + 2(-2) = 8. 4x - 4 = 8 4x = 12 x = 3 
Si termina con una ecuación sin variables y que no es verdadera (por ejemplo, 3 = 5), entonces el problema tiene sin solución. (Si ha graficado las ecuaciones, verá que son paralelas y nunca se cruzan). Si terminas con una ecuación sin variables, pero esas bien es verdadero (por ejemplo, 3 = 3), entonces el problema tiene un número infinito de soluciones. Las dos ecuaciones son exactamente iguales entre sí. (Si graficas las dos ecuaciones, verás que se superponen exactamente). 

Supongamos que tiene el sistema de ecuaciones 3x - y = 3 y -x + 2y = 4. Modifiquemos la primera ecuación para que la variable y está siendo eliminado. (También puede hacer esto para X hacer y obtener la misma respuesta). El - tu de la primera ecuación debe eliminarse con la+ 2 años ` en la segunda ecuación. Podemos hacer esto por - y multiplicar por 2. Multiplicamos ambos lados de la primera ecuación por 2, de la siguiente manera: 2(3x - y)=2(3), y por lo tanto 6x - 2y = 6. Ahora lo haré - 2 años caer contra el +2 años en la segunda ecuacion. 
Tus ecuaciones son: 6x - 2y = 6 y -x + 2y = 4. Combina los lados izquierdos: 6x - 2y - x + 2y = ? Combina los lados derechos: 6x - 2y - x + 2y = 6 + 4. 
Tienes: 6x - 2y - x + 2y = 6 + 4. Agrupa las variables X y y juntos: 6x - x - 2y + 2y = 6 + 4. Simplificar: 5x = 10 Solución para x: (5x)/5 = 10/5, de modo que x = 2. 
Tú lo sabes x = 2, y que una de tus ecuaciones originales 3x - y = 3 es. Introduce 2, en lugar de x: 3(2) - y = 3. Resolver para y en la ecuación: 6 - y = 3 6 - y + y = 3 + y, entonces 6 = 3 + y 3 = y 
Si su ecuación combinada no tiene variables y no es verdadera (como 2 = 7), entonces hay sin solución que se cumple para ambas ecuaciones. (Si graficas ambas ecuaciones, verás que son paralelas y nunca se cruzan). Si su ecuación combinada no tiene variables y es verdadera (como 0 = 0), entonces hay un número infinito de soluciones. Las dos ecuaciones son en realidad idénticas. (Si los pones en un gráfico, verás que se superponen por completo). 

La primera ecuación es: 2x + y = 5. Cambia esto a: y = -2x + 5. La segunda ecuación es: -3x + 6y = 0. cambiar esto a 6y = 3x + 0, y simplificar ay = ½x + 0. ¿Son ambas ecuaciones idénticas?, entonces toda la línea se convierte en una `intersección`. Escribir: infinitas soluciones. 
Si no tiene papel cuadriculado, use una regla para asegurarse de que los números estén espaciados uniformemente. Si usa números grandes o decimales, es posible que deba escalar el gráfico. (Por ejemplo 10, 20, 30 o 0.1, 0.2.0.3 en lugar de 1, 2, 3). 
En los ejemplos antes mencionados, una línea (y = -2x + 5) en el eje y 5. La otra línea (y = ½x + 0) pasa por el punto cero 0. (Estos son los puntos (0.5) y (0.0) en el gráfico). Marque cada una de las líneas con un color diferente, si es posible. 
En nuestro ejemplo, la regla y = -2x + 5 una pendiente de -2. En x = 1, la línea cae 2 abajodesde el punto x = 0. Dibuja el segmento de línea entre (0.5) y (1.3). La regla y = ½x + 0tiene una pendiente de ½. En x = 1, la línea va ½ arriba desde el punto x = 0. Dibuja el segmento de recta entre (0,0) y (1,½). si las rectas tienen la misma pendiente las líneas nunca se intersecarán, por lo que no hay solución para el sistema de ecuaciones. Escribir: sin solución. 
Si las líneas se mueven una hacia la otra, seguirás dibujando puntos en esa dirección. Si las líneas se alejan una de la otra, retrocede y dibuja puntos en la otra dirección, comenzando en x = -1. Si las líneas no están cerca una de la otra, avance y trace puntos más distantes, como x = 10. 
Resolver sistemas de ecuaciones con dos variables
Contenido
En un `sistema de ecuaciones` se le pide que resuelva dos o más ecuaciones al mismo tiempo. Cuando estos dos contienen variables diferentes, como x e y, o a y b, puede ser difícil a primera vista ver cómo resolverlos. Afortunadamente, una vez que sepa qué hacer, solo necesita algunas habilidades matemáticas básicas (y, a veces, algunos conocimientos de fracciones) para resolver el problema. Si es necesario, o si eres un aprendiz visual, también aprende a graficar las ecuaciones. Dibujar (trazar) un gráfico puede ser útil para "ver lo que está pasando" o para verificar su trabajo, pero también puede ser más lento que los otros métodos y no funcionará con todos los sistemas de ecuaciones.
Pasos
Método 1 de 3: usar el método de sustitución

1. Mover las variables a diferentes lados de la ecuación. Este método de `sustitución` comienza `resolviendo x` (o cualquier otra variable) en una de las ecuaciones. Por ejemplo, tenemos las siguientes ecuaciones: 4x + 2y = 8 y 5x + 3x = 9. Primero, veamos la primera ecuación. Reordena restando 2y de cada lado y obtienes: 4x = 8 - 2y.
- Este método a menudo usa fracciones en una etapa posterior. También puede usar el método de eliminación a continuación, si prefiere no trabajar con fracciones.

2. Divide ambos lados de la ecuación para `resolver x`. Una vez que tenga el término x (o cualquier variable que use) en un lado de la ecuación, divida ambos lados de la ecuación para aislar la variable. Por ejemplo:

3. Vuelva a conectar esto en la otra ecuación. Asegúrate de volver a la Otros comparación, no la que ya has usado. En esa ecuación, reemplazas la variable que resolviste para que solo quede una variable. Por ejemplo:

4. Resolver para la variable restante. Ahora tienes una ecuación con una sola variable. Usar técnicas comunes de álgebra para resolver esa variable. Si las variables se cancelan entre sí, continúe con el último paso. De lo contrario, terminará con una respuesta a una de sus variables:

5. Usa la respuesta para resolver la otra variable. No cometas el error de terminar el problema a la mitad. Tendrás que volver a ingresar la respuesta que obtuviste en una de las ecuaciones originales para que puedas resolver la otra variable:

6. Saber qué hacer cuando ambas variables se anulan entre sí. Cuando usted x = 3y + 2 u obtiene una respuesta similar en la otra ecuación, entonces intenta obtener una ecuación con una sola variable. A veces terminas con una ecuación en su lugar sin que Variables. Verifique dos veces su trabajo y asegúrese de sustituir la primera ecuación (reorganizada) en la segunda ecuación, no en la primera ecuación. Cuando esté seguro de que no ha cometido ningún error, obtendrá uno de los siguientes resultados:
Método 2 de 3: usar el método de eliminación
1. Determina la variable a eliminar. A veces, las ecuaciones se `eliminarán` entre sí en una variable tan pronto como las sume. Por ejemplo, cuando haces las ecuaciones 3x + 2y = 11 y 5x - 2y = 13 combina, el `+2y` y `-2y` se eliminarán entre sí, con todos los `ys se eliminan de la ecuación. Mire las ecuaciones en su problema para averiguar si alguna de las variables se eliminará de esta manera. Si no se elimina ninguna de las variables, lea el siguiente paso para obtener consejos.


2. Multiplicar una ecuación para eliminar una variable. (Omita este paso si las variables ya se han eliminado entre sí). Si ninguna de las variables en las ecuaciones se elimina por sí misma, entonces debe modificar una de las ecuaciones para que lo hagan. Esto es más fácil de entender con un ejemplo:

3. Combina las dos ecuaciones. Para combinar dos ecuaciones, suma los lados izquierdo y derecho. Si escribiste la ecuación correctamente, una de las variables debería cancelarse frente a la otra. Aquí hay un ejemplo usando las mismas ecuaciones que el último paso:

4. Resolver para la última variable. Simplifique la ecuación combinada, luego use álgebra básica para resolver la última variable. Si no quedan variables después de la simplificación, vaya al último paso de esta sección. De lo contrario, debería terminar con una respuesta simple a una de sus variables. Por ejemplo:

5. Resuelve para las otras variables. Has encontrado una variable, pero aún no has terminado. Sustituye tu respuesta en una de las ecuaciones originales para que puedas resolver la otra variable. Por ejemplo:

6. Saber qué hacer si ambas variables se anulan entre sí. A veces, la combinación de dos ecuaciones da como resultado una ecuación que no tiene sentido o no ayuda a resolver el problema. Revisa tu trabajo desde el principio, pero si no cometiste un error, escribe una de las siguientes respuestas:
Método 3 de 3: Graficar las ecuaciones

1. Solo use este método cuando se especifique. A menos que esté usando una computadora o una calculadora gráfica, muchos sistemas de ecuaciones solo se pueden resolver aproximadamente usando este método. Tu maestro o libro de texto de matemáticas puede pedirte que uses este método, por lo que probablemente estés familiarizado con ecuaciones gráficas como líneas. También puede usar este método para verificar si sus respuestas de uno de los otros métodos son correctas.
- La idea básica es que grafiques ambas ecuaciones y determines el punto donde se cruzan. Los valores de x e y en este punto dan el valor de x y el valor de y en el sistema de ecuaciones.

2. Resolver ambas ecuaciones para y. Manteniendo las dos ecuaciones separadas, usa álgebra para convertir cada ecuación a la forma `y = __x + __`. Por ejemplo:

3. Dibujar un sistema de coordenadas. En una hoja de papel cuadriculado, dibuje un `eje y` vertical y un `eje x` horizontal. Comience en el punto donde se cruzan las líneas y etiquete los números 1, 2, 3, 4, etc. arriba a lo largo del eje y y otra vez a la derecha a lo largo del eje x. Etiqueta los números -1, -2, etc. hacia abajo en el eje y y hacia la izquierda a lo largo del eje x.

4. Dibuja la intersección y para cada línea. Una vez que tienes una ecuación en la forma y = __x + __ puede comenzar a graficarlo, dibujando un punto donde la línea intercepta el eje y. Esto siempre tiene un valor de y, igual al último número en esta ecuación.

5. Usa la pendiente para seguir dibujando las líneas. En la forma y = __x + __, es el número para la x de Pendiente fuera de línea. Cada vez que x aumenta en uno, el valor de y aumentará en el valor de la pendiente. Usa esta información para encontrar el punto en el gráfico para cada línea, cuando x = 1. (Alternativamente, sustituya x = 1 por cualquier ecuación y resuelva para y).

6. Continúe trazando las líneas hasta que se crucen. Deténgase y mire su gráfico. Si las líneas ya se cruzaron entre sí, continúe con el siguiente paso. De lo contrario, toma una decisión en función de lo que hacen las líneas:

7. Encuentra la respuesta en la intersección de las rectas. Una vez que las dos rectas se cruzan, los valores de x e y en ese punto son la solución al problema. Si tienes suerte, la respuesta será un número entero. Por ejemplo, en nuestros ejemplos, las dos líneas se cruzan (2.1) así es tu respuesta x = 2 y y = 1. En algunos sistemas de ecuaciones, las líneas se intersecan en un valor entre dos números enteros y, a menos que su gráfico sea extremadamente preciso, será difícil saber dónde está. Si este es el caso, puede dar una respuesta como: `x está entre 1 y 2`. También puede usar el método de sustitución o el método de eliminación para encontrar la respuesta exacta.
Consejos
- Puede verificar su trabajo introduciendo las respuestas en las ecuaciones originales. Si las ecuaciones son verdaderas (por ejemplo, 3 = 3), entonces tu respuesta es correcta.
- En el método de eliminación, a veces tienes que multiplicar una ecuación por un número negativo para eliminar una variable.
Advertencias
- Estos métodos no se pueden usar cuando se trata de un número de potencia, como x. Para más información sobre ecuaciones de este tipo necesitas una guía para factorizar cuadrados con dos variables.
Artículos sobre el tema. "Resolver sistemas de ecuaciones con dos variables"
Оцените, пожалуйста статью
Popular