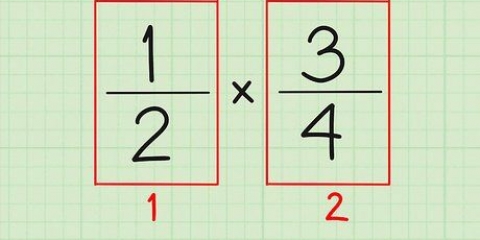
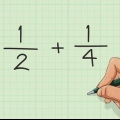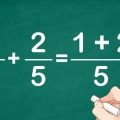Ex. 1: 1/4 + 2/4
Ex. 2: 3/8 + 2/8 + 4/8
Ex. 1: 1/4 + 2/4 es nuestra ecuación. "1" y"2" son los contadores. Eso significa 1 + 2 = 3.
Ex. 2: 3/8 + 2/8 + 4/8 es nuestra ecuación. "3" y"2" y"4" son los contadores. Eso significa 3 + 2 + 4 = 9.
Ex. 1: 3 es nuestro nuevo numerador, y 4 es el `nuevo` denominador. Esto da la respuesta: 3/4. 1/4 + 2/4 = 3/4.
Ex. 2: 9 es nuestro nuevo numerador, y 8 es el `nuevo` denominador. Esto da la respuesta: 9/8. 3/8 + 2/8 + 4/8 = 9/8.
Si el numerador es mayor que el denominador, como en p.ej. 2, entonces se puede quitar al menos un número entero de la fracción. Divide el numerador entre el denominador. Si dividimos 9 entre 8, obtenemos 1 entero y un resto de 1. Ponga el número entero antes de la fracción y el resto como el numerador de la nueva fracción, manteniendo el mismo denominador.9/8 = 1 1/8.

Ex. 3: 1/3 + 3/5
Ex. 4: 2/7 + 2/14
Ex. 3: 3 x 5 = 15. Ambas fracciones tienen 8 como denominador.
Ex. 4: 14 es múltiplo de 7. entonces solo tenemos que multiplicar 7 por 2 para obtener 14. Ambas fracciones tienen entonces un denominador de 14.
Ex. 3: 1/3 x 5/5 = 5/15.
Ex. 4: Para esta fracción solo necesitamos multiplicar la primera fracción por 2, porque de esta manera podemos obtener el denominador común.
2/7 x 2/2 = 4/14. Ex. 3: 3/5 x 3/3 = 9/15.
Ex. 4: La segunda fracción no necesita ser multiplicada porque ambas fracciones ya tienen el mismo denominador. Ex. 3: en lugar de 1/3 + 3/5, tenemos 5/15 + 9/15
Ex. 4: en lugar de 2/7 + 2/14, tenemos 4/14 + 2/14
Ex. 3: 5 + 9 = 14. 14 será el nuevo contador.
Ex. 4: 4 + 2 = 6. 6 será el nuevo contador.
Ex. 3: 15 será nuestro nuevo denominador.
Ex. 4: 14 será nuestro nuevo denominador.
Ex. 3: 14/15 es nuestra nueva respuesta a 1/3 + 3/5 = ?
Ex. 4: 6/14 es nuestra respuesta a 2/7 + 2/14 = ?
Ex. 3: 14/15 no se puede simplificar.
Ex. 4: 6/14 se puede reducir a 3/7 dividiendo tanto el numerador como el denominador por 2, el máximo común divisor.
Sumar fracciones juntas
Contenido
Ser capaz de sumar fracciones es una habilidad muy útil. No solo para la escuela primaria y secundaria, es solo una habilidad muy práctica. Lee más sobre sumar fracciones aquí. Te sorprenderá lo que puedes aprender en unos minutos.
Pasos
Método 1 de 2: primera parte: sumar fracciones con el mismo denominador

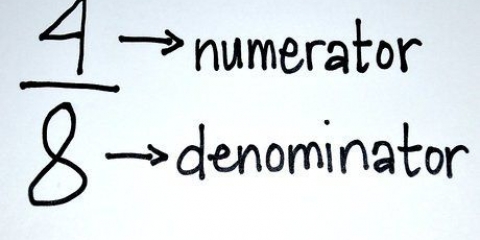
1. Revisa los denominadores (los números debajo de la línea) de cada fracción. Si tienen el mismo número, entonces estás tratando con fracciones con denominadores comunes. Si no, omita la siguiente sección.
2. Aquí hay dos ejemplos de problemas en los que trabajaremos en esta sección. Para cuando llegue al último paso, debe comprender cómo funciona la suma.


3. Toma los dos numeradores (los números arriba de la línea) y súmalos. No importa cuántas fracciones tengas, si tienen el mismo denominador puedes sumar todos los numeradores.


4. Construye la nueva fracción. Toma la suma de los numeradores que obtuviste en el Paso 2; esta suma se convierte el nuevo contador. Usa el denominador de las fracciones del paso anterior. Esto será el nuevo denominador; este denominador siempre permanece igual cuando sumas fracciones con el mismo denominador


5. Simplifica si puedes. Simplifica la nueva fracción para asegurarte de que los números sean lo más pequeños posible.

Método 2 de 2: Segunda parte: Sumar fracciones con denominadores desiguales

1. Verifique los denominadores (números debajo de la línea de fracción) de cada fracción. Si los denominadores son desiguales, entonces tienes que encontrar la manera de hacerlos iguales. Sigue leyendo para aprender.
2. Aquí hay dos ejemplos de problemas en los que trabajaremos en esta sección. Cuando lleguemos al último paso, sabrás cómo sumar fracciones con distinto denominador.


3. Encuentre un denominador adecuado. Puedes hacer esto buscando el múltiplo común de los denominadores. Una manera fácil de encontrarlo es simplemente multiplicar ambos denominadores. Si uno de los denominadores es múltiplo del otro, entonces solo necesitas multiplicar esa otra fracción.


4. Multiplica ambos números de la primera fracción por el denominador de la segunda fracción. No hay cambio en el valor de la fracción; simplemente cambiamos el aspecto de la fracción. sigue siendo la misma fraccion.


5. Multiplica ambos números de la segunda fracción por el denominador de la primera fracción. Nuevamente, no cambiamos el valor de la fracción, solo lo que parece. sigue siendo la misma fraccion.

6. Coloque ambas fracciones una al lado de la otra con sus nuevos números. Todavía no se han agregado, solo un poco de paciencia! Lo que hemos hecho es multiplicar cada fracción por un número apropiado, con el objetivo de igualar ambos denominadores.


7. Suma los numeradores de ambas fracciones.


8. Tome el denominador igual que calculó en el Paso 2 y utilícelo como el denominador de la nueva fracción. Por cierto, este es, por supuesto, el mismo denominador que ya ves en la fracción modificada.




9. simplifica la fraccion. Simplifica la fracción dividiendo el numerador y el denominador por el máximo común divisor.


Consejos
Artículos sobre el tema. "Sumar fracciones juntas"
Оцените, пожалуйста статью
Popular